1. Introduction
In the next 4 parts of this series, we look at various ring signature schemes and prove their security in the RO model. This part is dedicated to the analysis of a generic class of ring signature schemes introduced in [1] and inspired by [2]. We also introduce a specific instance of the generic scheme which is itself a generalization of the non-interactive Schnorr signature.
2. Herranz & Saèz generic scheme
The scheme is built on a security parameter ![]() , which by design corresponds to the length in bits of the output of the random oracle
, which by design corresponds to the length in bits of the output of the random oracle ![]() . Given a message
. Given a message ![]() and a ring
and a ring ![]() of
of ![]() members, the signing algorithm
members, the signing algorithm ![]() outputs a signature
outputs a signature ![]() where:
where:
- The
 ‘s are pairwise-different random elements chosen from a pre-defined large set. The term pairwise-different means that
‘s are pairwise-different random elements chosen from a pre-defined large set. The term pairwise-different means that 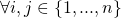 ,
,  .
. 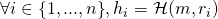 . That means that
. That means that 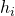 is the RO’s output on query
is the RO’s output on query 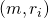 .
.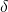 is fully determined by
is fully determined by  , and
, and 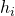 , for all
, for all 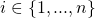 .
.
By design, we require that the probability of selecting any particular ![]() be upper-bounded by
be upper-bounded by ![]() . For example, consider the finite field
. For example, consider the finite field ![]() over a large prime
over a large prime ![]() . The probability of choosing a particular value for
. The probability of choosing a particular value for ![]() in the mutiplicative cyclic group
in the mutiplicative cyclic group ![]() is equal to
is equal to ![]() (assuming a uniform distribution over
(assuming a uniform distribution over ![]() ). Clearly, this is less than or equal to
). Clearly, this is less than or equal to ![]() .
.
