1. Introduction
In the next few parts of this series, we look at various signature schemes and prove their security in the RO model. This part is dedicated to the analysis of Pointcheval and Stern Generic Signature Scheme of which the Schnorr scheme is an example. The generic scheme is built around a single ![]() pair. Later parts of this series will focus on ring signature schemes. Ring signatures embed the actual signer in a ring of other possible signers to hide her identity. We will discuss them in parts 3, 4, 5, 6, and 7.
pair. Later parts of this series will focus on ring signature schemes. Ring signatures embed the actual signer in a ring of other possible signers to hide her identity. We will discuss them in parts 3, 4, 5, 6, and 7.
2. Pointcheval and Stern generic signature scheme
For a given message ![]() , our generic scheme creates a signature
, our generic scheme creates a signature ![]() where
where ![]() is a random element chosen from a pre-defined set,
is a random element chosen from a pre-defined set, ![]() (i.e., RO output on query
(i.e., RO output on query ![]() ), and
), and ![]() is fully determined by
is fully determined by ![]() and
and ![]() . By design, we require that the probability of selecting any particular
. By design, we require that the probability of selecting any particular ![]() be upper-bounded by
be upper-bounded by ![]() for a given security parameter
for a given security parameter ![]() .
.
Schnorr’s signature scheme is an example that fits this generic model. To see why, recall that ![]() chooses a random commitment
chooses a random commitment ![]() where
where ![]() is a pre-defined prime number. It then assigns
is a pre-defined prime number. It then assigns ![]() where
where ![]() denotes a chosen generator of
denotes a chosen generator of ![]() . Afterwards,
. Afterwards, ![]() is set to
is set to ![]() . Finally,
. Finally, ![]() is calculated as
is calculated as ![]() where
where ![]() denotes the signer’s private key. Note that
denotes the signer’s private key. Note that ![]() can be any element of
can be any element of ![]() and so the probability that it takes on a specific value is equal to
and so the probability that it takes on a specific value is equal to ![]() . By design, we choose the security parameter
. By design, we choose the security parameter ![]() . This choice of
. This choice of ![]() guarantees that the aforementioned probability is upper-bounded by
guarantees that the aforementioned probability is upper-bounded by ![]() .
.
3. Security analysis – Unforgeability vis-a-vis EFACM
For unforgeability proofs, we follow the 5-step approach mentioned in part 1 of this series.
Step 1: To prove that this generic scheme is secure against EFACM in the RO model, we proceed by contradiction and assume that there exists a PPT adversary ![]() such that:
such that:
Step 2: Next, we build a simulator ![]() such that it:
such that it:
- Does not have access to the private key of any signer.
- Has the same range as
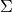 (i.e., they output signatures taken from the same pool of potential signatures over all possible choices of RO functions and respective random tapes
(i.e., they output signatures taken from the same pool of potential signatures over all possible choices of RO functions and respective random tapes  and
and  ).
). - Has indistinguishable probability distribution from that of
 over this range.
over this range.
![]() is specific to the particular instance of the generic scheme being used. In what follows, we build a simulator for the case of a Schnorr signature.
is specific to the particular instance of the generic scheme being used. In what follows, we build a simulator for the case of a Schnorr signature.
By construction, the output of ![]() will satisfy the verification equations. Moreover, it assigns a random value for
will satisfy the verification equations. Moreover, it assigns a random value for ![]() and bypasses the RO in doing so. Next, note the following:
and bypasses the RO in doing so. Next, note the following:
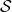 does not use any private key.
does not use any private key.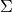 and
and 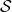 both have a range
both have a range
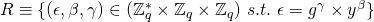 .
.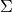 and
and 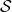 have the same probability distribution over
have the same probability distribution over 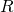 . Indeed,
. Indeed, 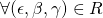 we have:
we have:
- For
![Rendered by QuickLaTeX.com \Sigma: P[(r,h,\alpha) = (\epsilon, \beta, \gamma)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-02c38ac68cc87ef443479c51b5712bce_l3.png)
![Rendered by QuickLaTeX.com = P_{k \neq 0, h}[g^{k} = \epsilon, h=\beta, k-hx = \gamma] = \frac{1}{(q-1).q}](https://delfr.com/wp-content/ql-cache/quicklatex.com-44cf7e7a6e267a140555b3f4d3e7239b_l3.png)
- For
![Rendered by QuickLaTeX.com \mathcal{S}: P[(r^{\sim},h^{\sim},\alpha^{\sim})=(\epsilon, \beta, \gamma)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-dfac7fd91f66c9b3f0e5148e7e073e55_l3.png)
![Rendered by QuickLaTeX.com = P_{r^{\sim}, h^{\sim}}[r^{\sim} \equiv g^{k}y^{h^{\sim}} = \epsilon, h^{\sim}=\beta, \alpha^{\sim} \equiv k = \gamma] = \frac{1}{(q-1).q}](https://delfr.com/wp-content/ql-cache/quicklatex.com-101cf182080fe59c2a42cf9996a3da1f_l3.png)
- For
With ![]() adequately built for the Schnorr scheme, we conclude that (refer to section 6 of part 1 of this series for a justification):
adequately built for the Schnorr scheme, we conclude that (refer to section 6 of part 1 of this series for a justification):
Step 3: We now show that the probability of faulty collisions is negligible (refer to section 6 of part 1 of this series for a description of collision types). The 2 types of collisions fo the generic scheme are:
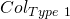 : A tuple
: A tuple 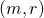 that
that 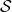 encounters — it makes its own random assignment to
encounters — it makes its own random assignment to 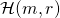 and bypasses RO — also appears in the list of queries that
and bypasses RO — also appears in the list of queries that 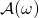 sends to RO. A conflict in the 2 values will happen with overwhelming probability and the execution will halt.
sends to RO. A conflict in the 2 values will happen with overwhelming probability and the execution will halt.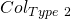 : A tuple
: A tuple 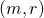 that
that 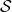 encounters — it makes its own random assignment to
encounters — it makes its own random assignment to 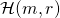 — is the same as another tuple
— is the same as another tuple 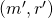 that
that 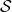 encountered at an earlier time instance — here too,
encountered at an earlier time instance — here too, 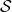 would have made its own random assignment to
would have made its own random assignment to 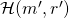 . Since the 2 tuples are identical (i.e.,
. Since the 2 tuples are identical (i.e., 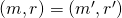 ), it must be that the 2 random assignments match (i.e.,
), it must be that the 2 random assignments match (i.e., 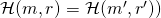 . With overwhelming probability, the 2 values will be different and the execution will halt.
. With overwhelming probability, the 2 values will be different and the execution will halt.
The aforementioned collisions must be avoided. In order to do so, we first calculate the probability of their occurence. We assume that during an EFACM attack, ![]() can make a maximum of
can make a maximum of ![]() queries to RO and a maximum of
queries to RO and a maximum of ![]() queries to
queries to ![]() .
. ![]() and
and ![]() are both assumed to be polynomial in the security parameter
are both assumed to be polynomial in the security parameter ![]() , since the adversary is modeled as a PPT Turing machine.
, since the adversary is modeled as a PPT Turing machine.
Next, we compute ![]() :
:
Step 4: In this step, our objective is to show that if ![]() is a successful tuple that generated a first EFACM forgery, then the following quantity is non-negligible in
is a successful tuple that generated a first EFACM forgery, then the following quantity is non-negligible in ![]() :
:
Here ![]() is an appropriate index that we will define in the proof. And to further simplify the notation, we let
is an appropriate index that we will define in the proof. And to further simplify the notation, we let ![]() and
and ![]() . (
. (![]() and
and ![]() denote respectively the
denote respectively the ![]() query to
query to ![]() and
and ![]() ) for all
) for all ![]() .
.
Let’s take a closer look at ![]() .
.
Any successful forgery must pass the verification test. One of the verification equations is to check if ![]() . So we distinguish between 2 scenarios (w.l.o.g. we assume that all
. So we distinguish between 2 scenarios (w.l.o.g. we assume that all ![]() -queries sent to RO are distinct from each-other since
-queries sent to RO are distinct from each-other since ![]() can keep a local copy of previous query results and avoid redundant calls):
can keep a local copy of previous query results and avoid redundant calls):
- Scenario 1:
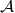 was successful in its forgery, and no collisions occured, and it never queried RO on input
was successful in its forgery, and no collisions occured, and it never queried RO on input 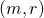 .
. - Scenario 2:
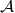 was successful in its forgery, and no collisions occured, and it queried RO on input
was successful in its forgery, and no collisions occured, and it queried RO on input 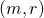 during its execution.
during its execution.
The probability of scenario 1 is upperbounded by the probability that ![]() picks a value for
picks a value for ![]() that matches the value of
that matches the value of ![]() . Here,
. Here, ![]() is the value that RO returns to
is the value that RO returns to ![]() (the verification algorithm) when verifying the validity of the forged signature. (It is upper-bounded because at the very least, the constraint
(the verification algorithm) when verifying the validity of the forged signature. (It is upper-bounded because at the very least, the constraint ![]() must be observed for a valid signature). And since
must be observed for a valid signature). And since ![]() can be any value in
can be any value in ![]() , we get:
, we get:
So we assume that a successful forgery will likely be of the Scenario 2 type. We have:
We then define ![]() to be the index of the query
to be the index of the query ![]() sent by
sent by ![]() to RO during execution. We let
to RO during execution. We let ![]() if the query
if the query ![]() was never asked by
was never asked by ![]() . This definition allows us to build the following sets:
. This definition allows us to build the following sets:
-
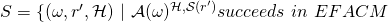
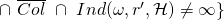
In other terms,
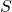 is the set of tuples
is the set of tuples 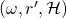 that yield a successful EFACM forgery when no collisions occur, and when
that yield a successful EFACM forgery when no collisions occur, and when 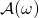 queried RO on input
queried RO on input 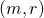 at some point during its execution (i.e., scenario 2).
at some point during its execution (i.e., scenario 2). -
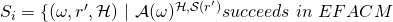
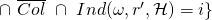
In other terms,
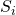 is the set of tuples
is the set of tuples 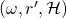 that yield a successful EFACM forgery when no collisions occur, and when the index of the
that yield a successful EFACM forgery when no collisions occur, and when the index of the 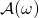 -query on input
-query on input 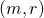 sent to RO is equal to
sent to RO is equal to 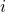 .
.
Recall that, ![]() , which is non-negligible in
, which is non-negligible in ![]() .
.
And ![]() partitions
partitions ![]() . So
. So ![]() .
.
This implies that ![]() .
.
If this were not the case, then one would get the following contradiction:
So we introduce the set ![]() consisting of all indices that meet the
consisting of all indices that meet the ![]() threshold, i.e.
threshold, i.e.
We claim that ![]() .
.
Proof: By definition of the sets ![]() we have:
we have:
The next step is to apply the splitting lemma to each ![]() . First note that:
. First note that:
Referring to the notation used in the splitting lemma (section 7 of part 1), we let:
![]() is defined as the space of tuples of all random tapes
is defined as the space of tuples of all random tapes ![]() , all random tapes
, all random tapes ![]() , and all possibe RO answers to the first
, and all possibe RO answers to the first ![]() queries sent by
queries sent by ![]() .
. ![]() is defined as the space of all possible RO answers to the last
is defined as the space of all possible RO answers to the last ![]() queries sent by
queries sent by ![]() . The splitting lemma guarantees the existence of a subset
. The splitting lemma guarantees the existence of a subset ![]() of tuples
of tuples ![]() such that:
such that:
![Rendered by QuickLaTeX.com P_{\omega,r',\mathcal{H}}[(\omega, r', \mathcal{H}) \in \Omega_i] \geq \frac{\nu(k)}{4Q}](https://delfr.com/wp-content/ql-cache/quicklatex.com-ce07e2bb293c71db559221e1667f7170_l3.png)
![Rendered by QuickLaTeX.com \forall [(\omega^{\sim}, r'^{\sim}, \mathcal{H}^{\sim}) \equiv (\omega^{\sim}, r'^{\sim}, \rho_1^{\sim}, ..., \rho_{i-1}^{\sim}, \rho_i^{\sim} ... \rho_Q^{\sim}]) \in \Omega_i](https://delfr.com/wp-content/ql-cache/quicklatex.com-06994a99771db59c0fb61c2766f6fe58_l3.png) , we have
, we have
![Rendered by QuickLaTeX.com P_\mathcal{H}[(\omega^{\sim}, r'^{\sim}, \rho_1^{\sim}, ..., \rho_{i-1}^{\sim}, \rho_i ... \rho_Q) \in S_i\ |\ (\omega^{\sim}, r'^{\sim}, \mathcal{H}^{\sim}) \in \Omega_i]](https://delfr.com/wp-content/ql-cache/quicklatex.com-1f73926a2612d2346e0be463d6a7fe6a_l3.png)
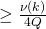 , and so
, and so![Rendered by QuickLaTeX.com P_\mathcal{H}[(\omega^{\sim}, r'^{\sim}, \mathcal{H}) \in S_i\ |\ (\omega^{\sim}, r'^{\sim}, \mathcal{H}^{\sim}) \in \Omega_i ,\ \rho_1 = \rho_1^{\sim}, ..., \rho_{i-1} = \rho_{i-1}^{\sim})]](https://delfr.com/wp-content/ql-cache/quicklatex.com-5bc0eb0dae1eca49b595a44540c3aae3_l3.png)
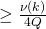
![Rendered by QuickLaTeX.com P[(\omega, r', \mathcal{H}) \in \Omega_i\ |\ (\omega, r', \mathcal{H}) \in S_i] \geq (\frac{\nu(k)}{4Q}) / (\frac{\nu(k)}{2Q}) = \frac{1}{2}](https://delfr.com/wp-content/ql-cache/quicklatex.com-8b4d252e6c6e0cf6594c44c987a7bd8e_l3.png)
We would like to compute the probability of finding a ![]() successful tuple
successful tuple ![]() given that
given that ![]() was a successful
was a successful ![]() tuple and s.t.
tuple and s.t. ![]() . That means finding the following probability:
. That means finding the following probability:
From the splitting lemma results, we have a (non-negligible in ![]() ) lower-bound on
) lower-bound on ![]() .
.
Note however, that ![]() and
and ![]() are generally distinct sets. And so we cannot conclude that
are generally distinct sets. And so we cannot conclude that
and therefore we cannot conclude that the following quantity is non-negligible in ![]()
In order to show that the above quantity is non-negligible in ![]() , we proceed differently. Suppose we can show that the following probability is non-negligible in
, we proceed differently. Suppose we can show that the following probability is non-negligible in ![]() :
:
This would imply that with non-negligible probability, we can find a tuple that belongs to ![]() (and hence corresponds to a successful forgery) and at the same time belongs to
(and hence corresponds to a successful forgery) and at the same time belongs to ![]() . We can then invoke the splitting lemma result just mentioned, to find a second tuple coresponding to a second forgery and that has the desired properties.
. We can then invoke the splitting lemma result just mentioned, to find a second tuple coresponding to a second forgery and that has the desired properties.
To prove the above, we proceed as follows:
And so we conclude that:
So let ![]() be such an index and
be such an index and ![]() such a tuple. From the result above, we know that finding such a
such a tuple. From the result above, we know that finding such a ![]() can be done with non-negligible probability. And since
can be done with non-negligible probability. And since ![]() , we must have
, we must have ![]() . We can then invoke the
. We can then invoke the ![]() consequence of the splitting lemma, and write:
consequence of the splitting lemma, and write:
We still have one last constraint to impose and that is that ![]() . We show that the following quantity is non-negligible:
. We show that the following quantity is non-negligible:
To prove this, note that if ![]() and
and ![]() are independent events, then we can write:
are independent events, then we can write:
And so we get ![]() . This results allows us to write:
. This results allows us to write:
Step 5: The final step uses the 2 forgeries obtained earlier to solve an instance of the Discrete Logarithm (DL) problem. Here is a recap of Step 4 results:
- With non-negligible probability of at least
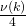 we get a successful tuple
we get a successful tuple 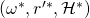 , s.t.
, s.t. 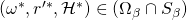 for some index
for some index 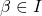 . So by running
. So by running 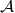 a number of times polynomial in
a number of times polynomial in 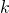 , we can confidently find such a tuple.
, we can confidently find such a tuple. - Once we find such a tuple, we’ve also shown that with non-negligible probability of at least
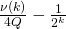 , we can find another successful tuple
, we can find another successful tuple 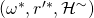 such that
such that 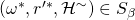 and
and 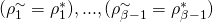 , but
, but 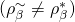 .
.
W.l.o.g, let ![]() correspond to
correspond to ![]() , and
, and ![]() correspond to
correspond to ![]() .
.
Recall that ![]() is the index of the query
is the index of the query ![]() that
that ![]() sends to the RO. Since the 2 experiments corresponding to the 2 successful tuples have the same random tapes
sends to the RO. Since the 2 experiments corresponding to the 2 successful tuples have the same random tapes ![]() and
and ![]() , and since the 2 corresponding ROs
, and since the 2 corresponding ROs ![]() and
and ![]() behave the same way on the first
behave the same way on the first ![]() queries, we can be confident that the first
queries, we can be confident that the first ![]() queries sent to the 2 ROs are identical. In particular the two
queries sent to the 2 ROs are identical. In particular the two ![]() queries are the same (i.e.,
queries are the same (i.e., ![]() . Moreover by design,
. Moreover by design, ![]() .
.
So we have 2 successful forgeries ![]() and
and ![]() , with
, with ![]() . Since both are valid signatures, they must satisfy the verification equations. For the particular case of a Schnorr signature scheme , they must satisfy the following 2 equations (1 verification equation per signature):
. Since both are valid signatures, they must satisfy the verification equations. For the particular case of a Schnorr signature scheme , they must satisfy the following 2 equations (1 verification equation per signature):
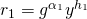 , where
, where 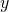 is the public key of the signer whose signature
is the public key of the signer whose signature 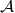 is forging.
is forging.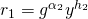 , where
, where 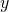 is the public key of the signer whose signature
is the public key of the signer whose signature 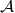 is forging.
is forging.
Writing ![]() (
(![]() is the secret key of the signer whose signature
is the secret key of the signer whose signature ![]() is forging), we get:
is forging), we get:
Since, ![]() , we can solve for
, we can solve for ![]() (the DL of
(the DL of ![]() ) in polynomial time. This contradicts the intractability of DL on multiplicative cyclic groups and we conclude that our signature scheme (in this case the Schnorr’s scheme) is secure against EFACM in the RO model.
) in polynomial time. This contradicts the intractability of DL on multiplicative cyclic groups and we conclude that our signature scheme (in this case the Schnorr’s scheme) is secure against EFACM in the RO model.
References
[1] D. Pointcheval and J. Stern. Security arguments for digital signatures and blind signatures. Journal of Cryptology, 2000.
Tags: Correctness, Privacy, Schnorr, Security, Signature, Unforgeability

No comments
Comments feed for this article
Trackback link: https://delfr.com/pointcheval-stern-generic-signature-scheme-monero-part-2-10/trackback/