1. Introduction
In this post we analyze two sources of divergence on the blockchain caused respectively by a natural fork and a malicious fork. The revolution that has been brought about by Bitcoin’s blockchain is a direct result of its open nature. Indeed, anyone can be part of it, suggest changes to it, mine new blocks in it, or simply conduct routine validations on it. It is in many respects, the epitome of decentralization and censorship-resistance. Its appealing nature is in large part rooted in its rich interdisciplinary foundation that spans across philosophy, mathematics and economics.
But beyond the elegance of its theoretical underpinning, the blockchain’s seamless implementation rests on an inherent agreement between its different participants. Without agreement, this harmonious apparatus would likely decay into chaos. The rather flawless operation of the system is the result of a particular consensus protocol known as Proof of Work (or PoW for short).
The consensus is meant to be amongst all of the miners on the network. It stipulates that any miner always extend the chain of blocks with the highest amount of cumulative work. In this context, work is a measure of the expected computational effort that a miner exerts in order to solve a given cryptographic challenge. In essence, the challenge consists in finding a value that makes the computation emit an output with a mandatory minimum number ![]() of leading 0’s. The work associated with mining a given block corresponds to the value
of leading 0’s. The work associated with mining a given block corresponds to the value ![]() where
where ![]() is dynamically adjusted to ensure that the network’s average block rate remains constant at
is dynamically adjusted to ensure that the network’s average block rate remains constant at ![]() 0.00167 blocks / second (i.e., 1 block per 10 minutes). We discuss PoW as well as other consensus protocols in more details in another post.
0.00167 blocks / second (i.e., 1 block per 10 minutes). We discuss PoW as well as other consensus protocols in more details in another post.
In an ideal setting where all miners are honest (i.e., abide by the PoW consensus protocol) and where blocks are propagated instantaneously on the network, all the nodes will always have a unified view of the blockchain — barring the extremely unlikely scenario of two distinct miners generating two valid blocks at the exact same time). However, imperfections do exist:
- Imperfection #1: The network incurs an information propagation delay. As a result, every new block takes a positive amount of time to reach all the other nodes on the network.
- Imperfection #2: There exists a subset of dishonest miners that decide to disregard the PoW consensus protocol. As a result, such miners can fork the blokchain and start mining on top of a parallel chain different than the one with the highest amount of cumulative work.
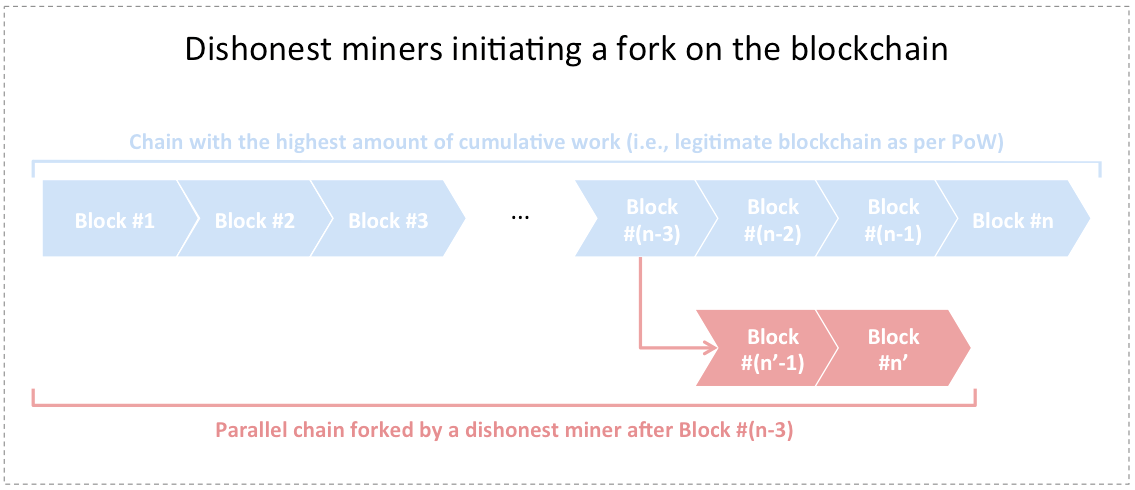
In the first case, miners are bound to momentarily experience diverging views of the blockchain. Even if all miners were honest, a network propagation delay would still cause natural forks to form on the blockchain. This is not desirable because one of the most important tenets of a well-functioning ledger consists in ensuring a unified view of the state of the system at any point in time.
We will show in section 2 that the probability of a natural fork occuring at some point in time on a system incurring an information propagation delay is equal to 1. However, we prove that the probability of sustaining a natural fork over a certain time interval is upper-bounded by a quantity that decays exponentially with the length of the interval. Consequently, any natural fork will collapse within finite time with high likelihood. A blockchain subject to the PoW consensus protocol is hence inclined to rapidly settle any natural fork that emerges.
In the second case, dishonest miners could stage an attack and maliciously attempt to redirect the blockchain to another chain of their liking and that suits their interest. The likelihood of success of such an attack (also known as a 51% attack) depends on the hashing power of the dishonest miner or pool of miners. We will discuss this case in section 3.
2. Probability of sustaining a natural fork when all miners are honest
We start by defining the following network parameters:
- Let
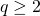 denote the total number of miners on the network. We let
denote the total number of miners on the network. We let  denote the
denote the  miner,
miner, 
- Let
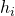 denote
denote  ‘s hashing power,
‘s hashing power,  And let
And let 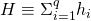 denote the network’s total hashing power.
denote the network’s total hashing power. - Let
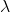 denote the network’s block rate in units of blocks per second. Moreover, let
denote the network’s block rate in units of blocks per second. Moreover, let  denote
denote  ‘s specific block rate,
‘s specific block rate, 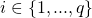 . Hence
. Hence 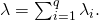
- Let
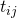 denote the average time in seconds it takes to propagate a block from
denote the average time in seconds it takes to propagate a block from  to
to 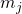 and vice versa (assuming symmetry). We define the network’s average propagation delay to be
and vice versa (assuming symmetry). We define the network’s average propagation delay to be 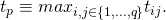 We also define the network’s average propagation unit to be
We also define the network’s average propagation unit to be 
- The probability that
 generates
generates 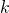 blocks (
blocks (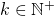 ) within an interval of
) within an interval of 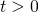 seconds follows a Poisson distribution with mean equal to
seconds follows a Poisson distribution with mean equal to 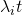 blocks. As a result,
blocks. As a result,  we have:
we have:
![]() generates
generates ![]() blocks within
blocks within ![]() seconds
seconds ![]()
We also define the following four events:
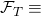 “At least one fork of the blockchain is formed at some point in time
“At least one fork of the blockchain is formed at some point in time ![Rendered by QuickLaTeX.com t_f \in (0, T]](https://delfr.com/wp-content/ql-cache/quicklatex.com-394cfe4d2de2f49e3f0e037a03e8ceb2_l3.png) “. The time origin
“. The time origin  can be chosen arbitrarily.
can be chosen arbitrarily.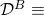 “A fork is formed at block #
“A fork is formed at block #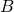 of the blockchain. All miners shared a unified view of the blockchain right before #
of the blockchain. All miners shared a unified view of the blockchain right before #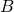 ‘s addition.”
‘s addition.” “A fork that was created at time
“A fork that was created at time  is sustained (i.e., does not collapse) for a minimum duration of
is sustained (i.e., does not collapse) for a minimum duration of 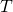 seconds right after its formation.”
seconds right after its formation.”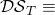 “A double-spend transaction coexists with the legitimate transaction,
“A double-spend transaction coexists with the legitimate transaction, 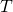 seconds after the latter got added to a certain block” (We will discuss this event in more details later in this section).
seconds after the latter got added to a certain block” (We will discuss this event in more details later in this section).
Note that in what follows, we make the following two assumptions:
- The PoW consensus protocol consists in extending the chain of blocks that has the highest amount of accumulated work. Theoretically, this is not equivalent to the longest chain (i.e., the chain with the highest number of blocks). However, for all practical matters, we assume that they are equivalent going forward.
- The block propagation delay
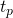 as defined earlier might be a large number since there might be nodes on the network that take a large amount of time on average to receive a given block. In general, block propagation statistics are described in terms of percentiles tracking how long it takes to propagate a block to a certain fraction of the network [2]. For all practical matters, we assume that
as defined earlier might be a large number since there might be nodes on the network that take a large amount of time on average to receive a given block. In general, block propagation statistics are described in terms of percentiles tracking how long it takes to propagate a block to a certain fraction of the network [2]. For all practical matters, we assume that 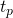 corresponds to the average time taken to propagate a block to 99% of the network.
corresponds to the average time taken to propagate a block to 99% of the network.
Our objective is four-fold:
- We first calculate the probability
![Rendered by QuickLaTeX.com P[\mathcal{F}_{\infty}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-ead7abf039bba2c62101007205fd54a5_l3.png) of a natural fork occuring at some point in time (assuming all miners are honest) and show it is equal to 1.
of a natural fork occuring at some point in time (assuming all miners are honest) and show it is equal to 1. - Second, we derive a non-trivial upper bound on
![Rendered by QuickLaTeX.com P[\mathcal{D}^B],](https://delfr.com/wp-content/ql-cache/quicklatex.com-bc1b66b0ee660caaf585d70cdc6a12d5_l3.png) for any given block
for any given block 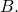
- Third, we derive a non-trivial upper bound on
![Rendered by QuickLaTeX.com P[\mathcal{S}_T],](https://delfr.com/wp-content/ql-cache/quicklatex.com-b8be7382a3f3ff444fdd00c7170e829f_l3.png) decaying exponentially in
decaying exponentially in 
- Finally, we derive a non-trivial upper bound on
![Rendered by QuickLaTeX.com P[\mathcal{DS}_T],](https://delfr.com/wp-content/ql-cache/quicklatex.com-d383596e53ee32c1d85de6485f058941_l3.png) by making use of the results of the preceding two points.
by making use of the results of the preceding two points.
Objective #1: Natural forks on the blockchain happen with probability 1:
- Choose
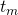 such that
such that  We can write:
We can write:
![Rendered by QuickLaTeX.com P[F_{\infty}] = lim_{n \rightarrow \infty} P[F_{nt_m}] = 1 - lim_{n \rightarrow \infty} P[\overline{F_{nt_m}}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-9475d51ae4c8a1ffff44f54b15fd6aa4_l3.png)
where
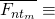 “No fork is formed on the blockchain at any time in the interval
“No fork is formed on the blockchain at any time in the interval ![Rendered by QuickLaTeX.com (0,nt_m]](https://delfr.com/wp-content/ql-cache/quicklatex.com-11dc85016b2488498939b4f98fc27499_l3.png) “
“  let
let 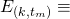 “No fork is formed on the blockchain at any time in the interval
“No fork is formed on the blockchain at any time in the interval ![Rendered by QuickLaTeX.com ((k-1)t_m,\ kt_m]](https://delfr.com/wp-content/ql-cache/quicklatex.com-3d83e4b90369a7e078d713c76db2c5f3_l3.png) “. We can then write:
“. We can then write:
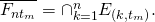
- Let
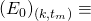 “None of the
“None of the 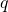 miners generate any block in the interval
miners generate any block in the interval ![Rendered by QuickLaTeX.com ((k-1)t_m,\ kt_m]](https://delfr.com/wp-content/ql-cache/quicklatex.com-3d83e4b90369a7e078d713c76db2c5f3_l3.png) “, and let
“, and let 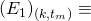 “One and only one miner out of
“One and only one miner out of 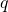 generates at least 1 block in the interval
generates at least 1 block in the interval ![Rendered by QuickLaTeX.com ((k-1)t_m,\ kt_m]](https://delfr.com/wp-content/ql-cache/quicklatex.com-3d83e4b90369a7e078d713c76db2c5f3_l3.png) “. We claim that:
“. We claim that:
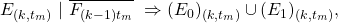 for all
for all 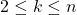
To see why, note that if both
 and
and 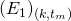 were not true, then there would exist at least two distinct miners that generate at least 1 block each in the interval
were not true, then there would exist at least two distinct miners that generate at least 1 block each in the interval ![Rendered by QuickLaTeX.com ((k-1)t_m,\ kt_m].](https://delfr.com/wp-content/ql-cache/quicklatex.com-43bfe49a55b77275bb462b3fa8692385_l3.png) But since
But since  it must be that at least two parallel blocks (one from each miner) coexist, hence forming a fork. Indeed, the choice of
it must be that at least two parallel blocks (one from each miner) coexist, hence forming a fork. Indeed, the choice of 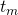 guarantees that none of the two blocks will have sufficient time to propagate to the other node. We conclude that
guarantees that none of the two blocks will have sufficient time to propagate to the other node. We conclude that 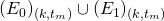 is a necessary condition for
is a necessary condition for 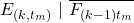 to hold. Observing that
to hold. Observing that  and
and 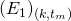 are disjoint, we get:
are disjoint, we get:![Rendered by QuickLaTeX.com P[E_{(k,t_m)}\ |\ \overline{F_{(k-1)t_m}}] \leq P[(E_0)_{(k,t_m)} \cup (E_1)_{(k,t_m)}] = P[(E_0)_{(k,t_m)}] + [(E_1)_{(k,t_m)}].](https://delfr.com/wp-content/ql-cache/quicklatex.com-e87d48c13220cbb32b2860b4fed52487_l3.png)
- We can calculate
![Rendered by QuickLaTeX.com P[(E_0)_{(k,t_m)}] =\Pi_{i =1}^q e^{- \lambda_i t_m} = e^{-\lambda t_m}.](https://delfr.com/wp-content/ql-cache/quicklatex.com-09a5274f89b6245e1c91cdf569136688_l3.png) This quantity is independent of
This quantity is independent of 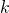 and so
and so ![Rendered by QuickLaTeX.com P[(E_0)_{(k,t_m)}] \equiv P[(E_0)_{t_m}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-220c644195a84b15a8e3dc367adc6e6b_l3.png)
- Similarly,
![Rendered by QuickLaTeX.com P[(E_1)_{(k,t_m)}] = \Sigma_{i=1}^q [(1 - e^{-\lambda_i t_m}) \Pi_{j = 1, j \neq i}^q e^{-\lambda_j t_m}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-3d6a0e23c78a9502ae5f8d0d70c6485f_l3.png)
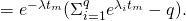
This is also independent of
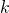 and so
and so ![Rendered by QuickLaTeX.com P[(E_1)_{(k,t_m)}] \equiv P[(E_1)_{t_m}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-176dc5ca8e57c27741135e3e2619c3d9_l3.png)
- Putting it altogether, we get:
![Rendered by QuickLaTeX.com P[\overline{F_{n \times t_m}}] = P[\cap_{k=1}^{n} E_{(k,t_m)}]\ =\ \Pi_{k=2}^{n}\ (P[E_{(k,t_m)}\ |\ \overline{F_{(k-1)t_m}}]) \times\ P[E_{(1,t_m)}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-446d97c518c8db1e28497af64edba49b_l3.png)
![Rendered by QuickLaTeX.com \leq \Pi_{k=2}^{n}\ (P[E_{(k,t_m)}\ |\ \overline{F_{(k-1)t_m}}])\ \leq\ \Pi_{k=2}^{n}\ (P[(E_0)_{t_m}] + P[(E_1)_{t_m}])](https://delfr.com/wp-content/ql-cache/quicklatex.com-e19f4b7e85470b39c0b4ca1bd8932cb6_l3.png)
![Rendered by QuickLaTeX.com = (P[(E_0)_{t_m}] + P[(E_1)_{t_m}])^{n-1}](https://delfr.com/wp-content/ql-cache/quicklatex.com-82a998c6a000f9d54c50a846a5ea565c_l3.png)
 let
let 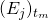 denote the event “
denote the event “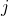 and only
and only 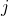 miners out of
miners out of 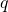 generate at least 1 block each in an interval of
generate at least 1 block each in an interval of 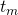 seconds”. One can easily see that for a finite value of
seconds”. One can easily see that for a finite value of 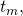
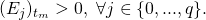 As a result, we have:
As a result, we have:
![Rendered by QuickLaTeX.com P[(E_0)_{t_m}] + P[(E_1)_{t_m}] < \Sigma_{j=0}^q P[(E_j)_{t_m}] = 1](https://delfr.com/wp-content/ql-cache/quicklatex.com-8e52e96a8dbb61a9a31dc75accc7b7aa_l3.png)
- Consequently, we get:
![Rendered by QuickLaTeX.com 0 \leq P[\overline{F_{\infty}}] = lim_{n \rightarrow \infty} P[\overline{F_{nt_m}}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-bf1b9f70cbe4f736a86d57ed8686add6_l3.png)
![Rendered by QuickLaTeX.com \leq lim_{n \rightarrow \infty} (P[(E_0)_{t_m}] + P[(E_1)_{t_m}])^{n-1} = 0](https://delfr.com/wp-content/ql-cache/quicklatex.com-f74e0d682de5b91f237e77953cc0abf4_l3.png)
And since
![Rendered by QuickLaTeX.com P[\overline{F_{\infty}}] = 0,](https://delfr.com/wp-content/ql-cache/quicklatex.com-f87b52ef676ee6df44add1a49f7f90f8_l3.png) we conclude that
we conclude that ![Rendered by QuickLaTeX.com P[F_{\infty}] = 1](https://delfr.com/wp-content/ql-cache/quicklatex.com-41ef60abc4699be07356330792ad1769_l3.png)
Objective #2: A non-trivial upper bound on the probability of a natural fork occuring at an arbitrary block:
Suppose that all miners share a unified view of the blockchain. At time ![]() one of the miners adds block #
one of the miners adds block #![]() to the blockchain. Miners that still haven’t received block #
to the blockchain. Miners that still haven’t received block #![]() (which for all practical matters could take up to
(which for all practical matters could take up to ![]() could generate their own block and start a fork at #
could generate their own block and start a fork at #![]() We are interested in computing the probability that such an event occurs, i.e.
We are interested in computing the probability that such an event occurs, i.e. ![]() We define the following:
We define the following:
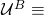 “No fork ever gets formed at block #
“No fork ever gets formed at block #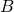 , knowing that all miners shared a unified view of the blockchain right before #
, knowing that all miners shared a unified view of the blockchain right before #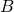 ‘s addition by some miner.”
‘s addition by some miner.”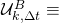 “None of the miners that still haven’t received block #
“None of the miners that still haven’t received block #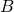 by time
by time 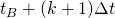 , generate any block in
, generate any block in ![Rendered by QuickLaTeX.com (t_B + k \Delta t,\ t_B + (k+1) \Delta t].](https://delfr.com/wp-content/ql-cache/quicklatex.com-7738f58ef35a9f89e3d9e4898055ab85_l3.png) “
“- Let
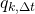 be the total number of miners out of a total of
be the total number of miners out of a total of 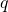 miners, that still haven’t seen block #
miners, that still haven’t seen block #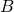 by time
by time 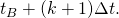 Let these miners be indexed as
Let these miners be indexed as 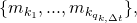 and let
and let 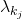 denote the block rate of miner
denote the block rate of miner 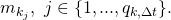
By letting ![]() we can write:
we can write:
![]()
And so letting ![]() we can write:
we can write:
![]()
![]()
Letting ![]() be the ratio of miners that still haven’t received block #
be the ratio of miners that still haven’t received block #![]() by time
by time ![]() we get:
we get:
![]()
![]()
Note that if all miners share the same block rate ![]() , then
, then ![]() As a result, we would get
As a result, we would get ![]() (note the equality in this case). For small
(note the equality in this case). For small ![]() this value can be approximated by
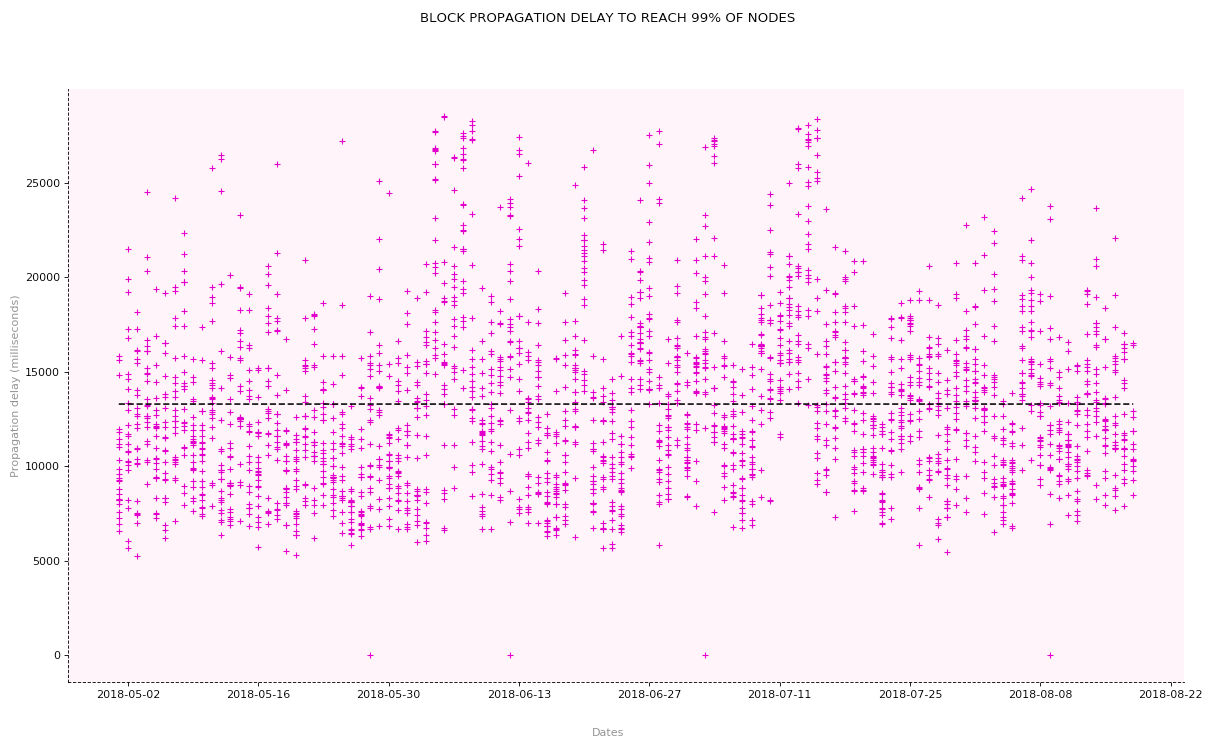
this value can be approximated by ![]() as found in [1]. Below is a representation of a block propagation delay as observed on the
as found in [1]. Below is a representation of a block propagation delay as observed on the ![]() of August 2018 [2]. In order to compute
of August 2018 [2]. In order to compute ![]() we make the assumption that the share of miners that still haven’t received the block by a certain time is the same as the corresponding share of generic nodes.
we make the assumption that the share of miners that still haven’t received the block by a certain time is the same as the corresponding share of generic nodes.

We find that ![]() Using
Using ![]() blocks/sec, we get
blocks/sec, we get
![]()
Objective #3: Natural forks collapse with high likelihood in a finite amount of time:
In what follows, we derive a non-trivial upper bound on ![]() To do so, we will first find a lower bound on the probability of occurrence of its complement
To do so, we will first find a lower bound on the probability of occurrence of its complement ![]() “A fork that was created at time
“A fork that was created at time ![]() collapses at some point in time in the interval
collapses at some point in time in the interval ![]() “. An adequate lower bound on
“. An adequate lower bound on ![]() would be given by
would be given by ![]() where
where ![]() is an event whose occurence is a sufficient condition for
is an event whose occurence is a sufficient condition for ![]() to hold true. Our objective becomes one of finding an appropriate
to hold true. Our objective becomes one of finding an appropriate ![]() and calculating a lower bound on
and calculating a lower bound on ![]()
In the tree below, we depict the different scenarios that lead to a natural fork formation, starting with a shared view of the blockchain. ![]() and
and ![]() are time instances corresponding to block formations by miners
are time instances corresponding to block formations by miners ![]() and
and ![]() respectively. Recall that
respectively. Recall that ![]() denotes the average block propagation time between
denotes the average block propagation time between ![]() and
and ![]() Scenarios that lead to a fork formation are one of two types: those that lead to parallel chains of equal length (i.e., Type 1) and those that lead to chains of different lengths (i.e., Type 2):
Scenarios that lead to a fork formation are one of two types: those that lead to parallel chains of equal length (i.e., Type 1) and those that lead to chains of different lengths (i.e., Type 2):
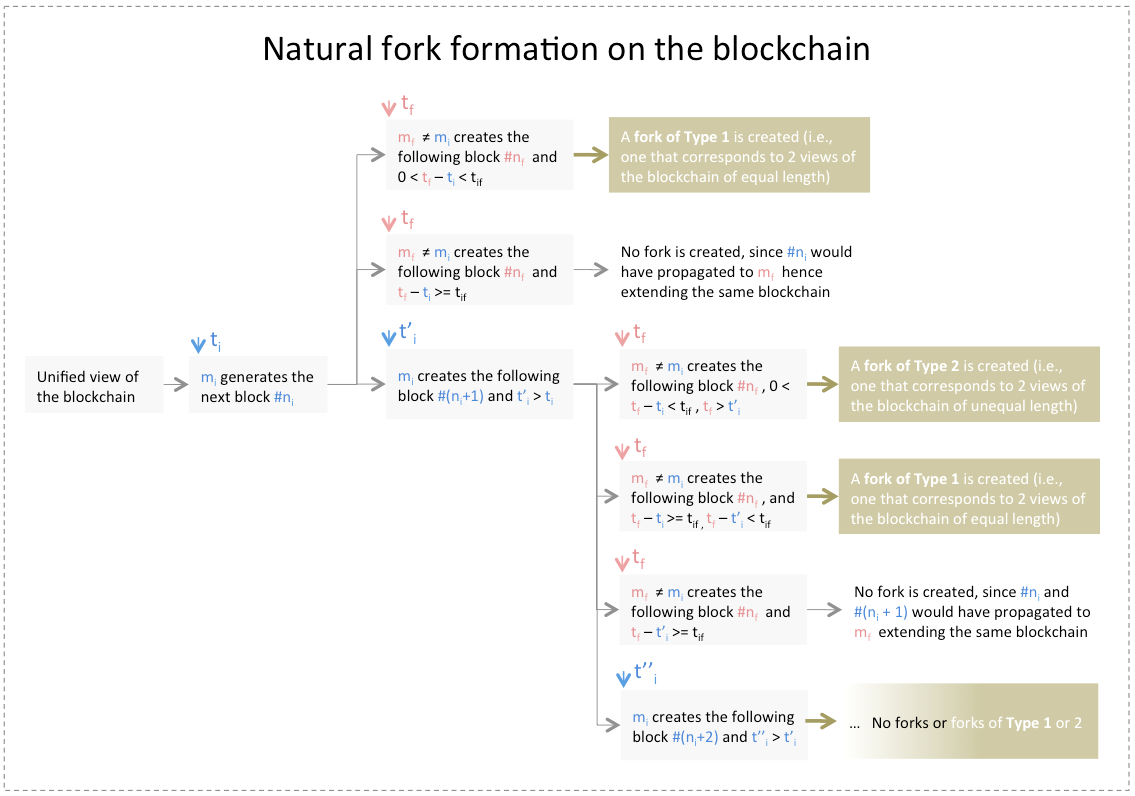
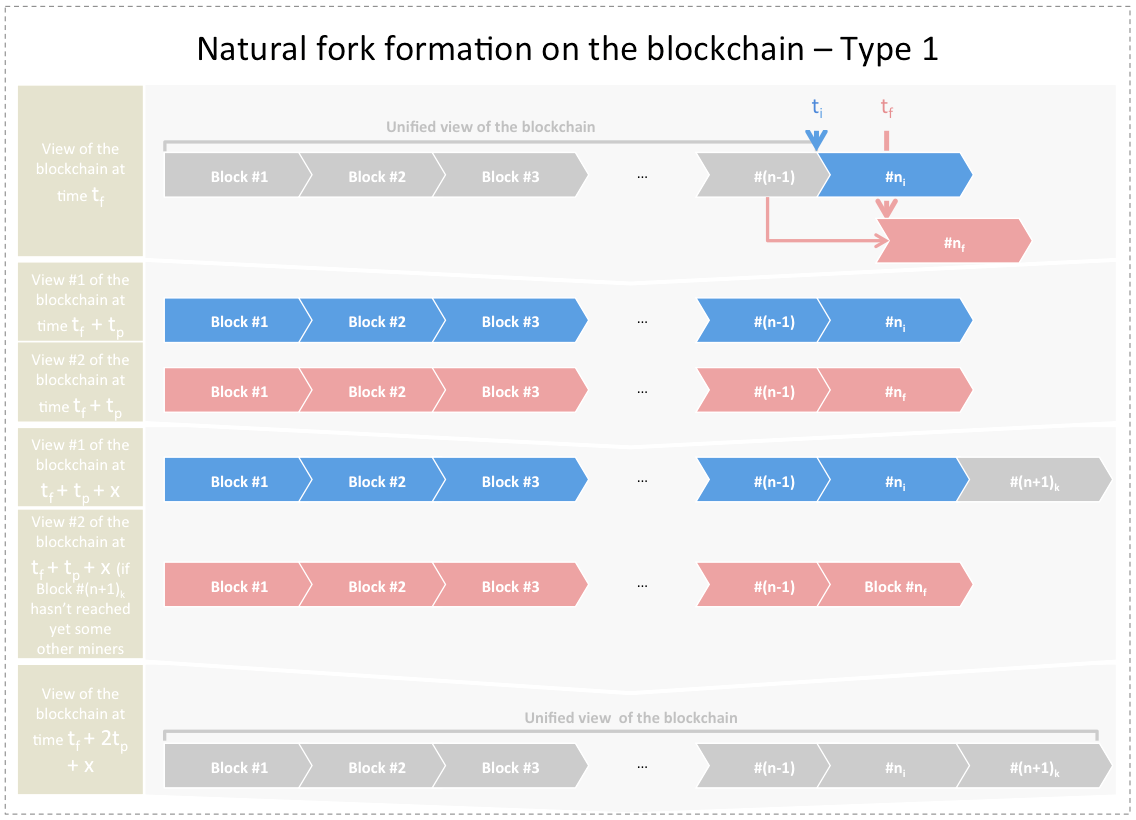
Forks of type 1: Before time ![]() all miners share the same view of the blockchain. At
all miners share the same view of the blockchain. At ![]() (for some
(for some ![]() generates block #
generates block #![]() At
At ![]() (for some
(for some ![]() generates the following block #
generates the following block #![]() such that
such that ![]() If we wait for
If we wait for ![]() seconds and no miner generates any block in interval
seconds and no miner generates any block in interval ![]() then at time
then at time ![]() there will be more than one view of the blockchain, all of which have the same length. If for the following
there will be more than one view of the blockchain, all of which have the same length. If for the following ![]() seconds (
seconds (![]() ), one and only one
), one and only one ![]() generates at least one block #
generates at least one block #![]() , and then for the following
, and then for the following ![]() seconds no miner generates any block, then by time
seconds no miner generates any block, then by time ![]() all forks would collapse. This is depicted in the figure below:
all forks would collapse. This is depicted in the figure below:
Forks of type 2: Before time ![]() all miners share the same view of the blockchain. At
all miners share the same view of the blockchain. At ![]() (for some
(for some ![]() generates block #
generates block #![]() At
At ![]() mines the next block #
mines the next block #![]() At
At ![]() (for some
(for some ![]() generates the following block #
generates the following block #![]() Two views of the blockchain will coexist at
Two views of the blockchain will coexist at ![]() with one being a longer chain than the other. If we wait for
with one being a longer chain than the other. If we wait for ![]() seconds, and no miner generates any block in interval
seconds, and no miner generates any block in interval ![]() then by
then by ![]() all forks would collapse. This is depicted in the figure below:
all forks would collapse. This is depicted in the figure below:
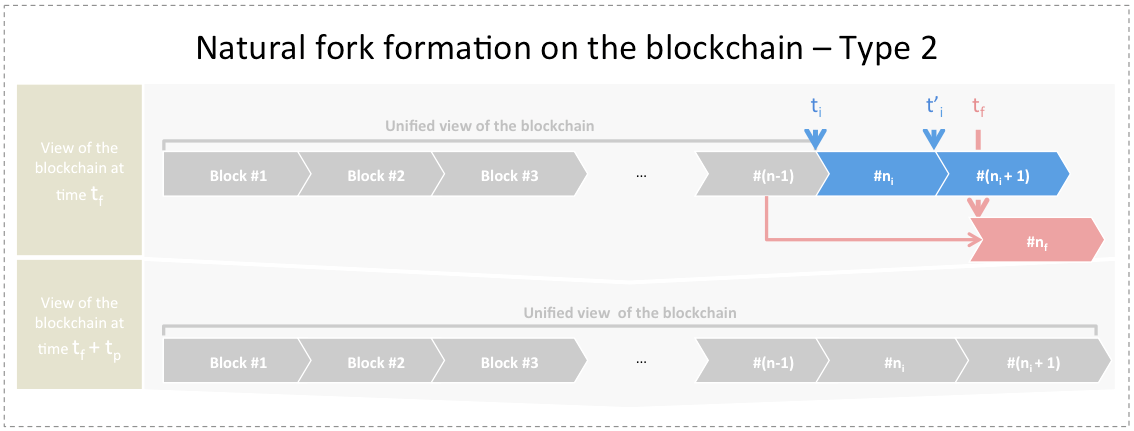
One consequence is that given a fork that was formed at time ![]() , if we ensure that for the next
, if we ensure that for the next ![]() seconds no miner generates any blocks, and that for the subsequent
seconds no miner generates any blocks, and that for the subsequent ![]() seconds one and only one miner generates at least 1 block, and finally for the subsequent
seconds one and only one miner generates at least 1 block, and finally for the subsequent ![]() seconds no miner generates any block, then the fork would collapse in the interval
seconds no miner generates any block, then the fork would collapse in the interval ![]() This construction ensures a sufficient condition for a fork to collapse within a specific time interval. In what follows, we formalize our approach:
This construction ensures a sufficient condition for a fork to collapse within a specific time interval. In what follows, we formalize our approach:
- Let
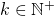 and let
and let 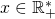 . We refer to
. We refer to 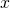 as the interval design parameter expressed in units of seconds. We define the following events:
as the interval design parameter expressed in units of seconds. We define the following events:
 “No miner out of
“No miner out of 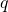 generates any block in the time interval
generates any block in the time interval ![Rendered by QuickLaTeX.com (t_f + k(x+2t_p),\ t_f + kx + (2k+1)t_p]](https://delfr.com/wp-content/ql-cache/quicklatex.com-1bf82d1e84f6a327b92d6b05ff55e9d9_l3.png) “
“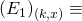 “One and only one miner out of
“One and only one miner out of 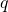 generates at least 1 block in the time interval
generates at least 1 block in the time interval ![Rendered by QuickLaTeX.com (t_f + kx + (2k+1)t_p,\ t_f + (k+1)x + (2k+1)t_p]](https://delfr.com/wp-content/ql-cache/quicklatex.com-59d9b26f0cfc57266122ef523cb84852_l3.png) “
“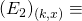 “No miner out of
“No miner out of 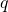 generates any block in interval
generates any block in interval ![Rendered by QuickLaTeX.com (t_f + (k+1)x + (2k+1)t_p,\ t_f + (k+1)(x + 2t_p)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-aa2806db53cd0d49f3b0ef219745f71a_l3.png) “
“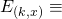 “Any fork that could have existed at time
“Any fork that could have existed at time  collapses at some time in the interval
collapses at some time in the interval ![Rendered by QuickLaTeX.com (t_f + k(x+2t_p),\ t_f + (k+1)(x+2t_p)].](https://delfr.com/wp-content/ql-cache/quicklatex.com-8238b80f1f41302a4a74bd8c588504d1_l3.png) “
“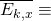 “At least one fork that existed at time
“At least one fork that existed at time  is sustained throughout
is sustained throughout ![Rendered by QuickLaTeX.com (t_f + k(x+2t_p),\ t_f + (k+1)(x+2t_p)].](https://delfr.com/wp-content/ql-cache/quicklatex.com-8238b80f1f41302a4a74bd8c588504d1_l3.png) “
“
- The previous logic allows us to conclude that if
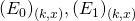 and
and 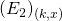 are all satisifed, then
are all satisifed, then 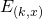 will hold true
will hold true 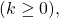 and so will
and so will 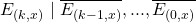
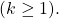 We conclude that the event
We conclude that the event 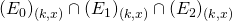 is a sufficient condition for the occurence of
is a sufficient condition for the occurence of 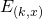
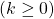 and
and 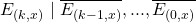 (
(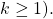 We get:
We get:
![Rendered by QuickLaTeX.com p[E_{(k,x)}],\ p[E_{(k,x)}\ |\ \overline{E_{(k-1,x)}},..., \overline{E_{(0,x)}}]\ \geq](https://delfr.com/wp-content/ql-cache/quicklatex.com-6f5267ea1cb0fd10cc6dc0692da59b6f_l3.png)
![Rendered by QuickLaTeX.com p[(E_0)_{(k,x)} \cap (E_1)_{(k,x)} \cap (E_2)_{(k,x)}] \equiv](https://delfr.com/wp-content/ql-cache/quicklatex.com-30bbe37d586d4a9e8bab5e37bd1fafe6_l3.png)
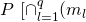 does not create any block in time interval
does not create any block in time interval ![Rendered by QuickLaTeX.com (t_f + k(x+2t_p),\ t_f + kx + (2k+1)t_p])](https://delfr.com/wp-content/ql-cache/quicklatex.com-3ed23c7b202c7ee34ac0f06778b05065_l3.png)
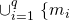 creates at least one block in time interval
creates at least one block in time interval ![Rendered by QuickLaTeX.com (t_f + kx + (2k+1)t_p,\ t_f + (k+1)x + (2k+1)t_p\ ]\cap_{j=1, j \neq i}^q(m_j](https://delfr.com/wp-content/ql-cache/quicklatex.com-6b4cfeaa257fca843d631f7892964052_l3.png) does not create any block in time interval
does not create any block in time interval ![Rendered by QuickLaTeX.com (t_f + kx + (2k+1)t_p,\ t_f + (k+1)x + (2k+1)t_p])\}](https://delfr.com/wp-content/ql-cache/quicklatex.com-8ca1bd97cc20ea9818d40aabf1618342_l3.png)
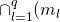 does not create any block in
does not create any block in ![Rendered by QuickLaTeX.com (t_f + (k+1)x + (2k+1)t_p,\ t_f + (k+1)(x + 2t_p)])\ ]](https://delfr.com/wp-content/ql-cache/quicklatex.com-061c952d2521f2173a5fffcc7308015b_l3.png)
Recognizing that all the events appearing under the union symbol above are disjoint, and that all the intersections are taken over independent events, we get:
![Rendered by QuickLaTeX.com p[E_{(k,x)}],\ p[E_{(k,x)}\ |\ \overline{E_{(k-1,x)}},..., \overline{E_{(0,x)}}] \geq](https://delfr.com/wp-content/ql-cache/quicklatex.com-bb89eecfdad7d55b653514ba33440616_l3.png)
![Rendered by QuickLaTeX.com [\Sigma_{i=1}^q (1-e^{-\lambda_i x}) e^{-(\lambda - \lambda_i)x}]e^{-2\lambda t_p}](https://delfr.com/wp-content/ql-cache/quicklatex.com-262ace5ef58fdf7b5fbef09820f04254_l3.png)
![Rendered by QuickLaTeX.com =\ e^{-\lambda (x + 2t_p)}[\Sigma_{i=1}^q e^{\lambda_i x}\ -\ q]](https://delfr.com/wp-content/ql-cache/quicklatex.com-47ab3f1a0219d8315ea70fa3e3ea266d_l3.png)
- Now note that
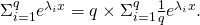 And since the exponential function is convex, we can invoke Jensen’s inequality to conclude that
And since the exponential function is convex, we can invoke Jensen’s inequality to conclude that  we have:
we have:

- As a result,

![Rendered by QuickLaTeX.com P[(E)_{(k,x)}],\ P[E_{(k,x)}\ |\ \overline{E_{(k-1,x)}},..., \overline{E_{(0,x)}}] \geq\ q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1]](https://delfr.com/wp-content/ql-cache/quicklatex.com-d43894652075be7449b3b3f61bfca50c_l3.png)
- And so
![Rendered by QuickLaTeX.com P[\overline{E_{(k,x)}}] = 1 - P[E_{(k,x)}] \leq 1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1]](https://delfr.com/wp-content/ql-cache/quicklatex.com-a09a30e65f75565e72141bf161ca1c9d_l3.png)
![Rendered by QuickLaTeX.com P[\overline{E_{(k,x)}}\ |\ \overline{E_{(k-1,x)}},..., \overline{E_{(0,x)}}] = 1 - P[E_{(k,x)}\ |\ \overline{E_{(k-1,x)}},..., \overline{E_{(0,x)}}] \leq](https://delfr.com/wp-content/ql-cache/quicklatex.com-ecc2c303f1b4b3d7cb6a4c6c9a25c957_l3.png)
![Rendered by QuickLaTeX.com 1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1]](https://delfr.com/wp-content/ql-cache/quicklatex.com-a6146cc61496d0e952659cac62627a4e_l3.png)
- Let
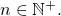 In order to sustain a fork over a minimum duration of
In order to sustain a fork over a minimum duration of 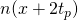 seconds after its formation at time
seconds after its formation at time 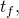 we must sustain it over each
we must sustain it over each ![Rendered by QuickLaTeX.com (t_f + k(x + 2t_p),\ t_f + (k+1)(x + 2t_p)],\ \forall k \in \{{0,...,n-1\}}.](https://delfr.com/wp-content/ql-cache/quicklatex.com-c125980119565538e1bc9231c8ec2066_l3.png) This implies that:
This implies that:
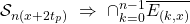
As a result,
 we can write:
we can write:![Rendered by QuickLaTeX.com P[\mathcal{S}_{n(x + 2t_p)}]\ \leq\ P[\cap_{k = 0}^{n-1} \overline{E_{(k,x)}}]\ =](https://delfr.com/wp-content/ql-cache/quicklatex.com-05715e2423d170316b8a521c679ac158_l3.png)
![Rendered by QuickLaTeX.com \Pi_{k=1}^{n-1} P[\overline{E_{(k,x)}}\ |\ \overline{E_{(k-1,x)}},.., \overline{E_{(0,x)}}]\ \times\ P[\overline{E_{(0,x)}}] \leq](https://delfr.com/wp-content/ql-cache/quicklatex.com-ff16feaf405ae59f9f7f397282e04414_l3.png)
![Rendered by QuickLaTeX.com (1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^n](https://delfr.com/wp-content/ql-cache/quicklatex.com-a8900bc33f71c475b7edaaecf154666d_l3.png)
And in particular,
![Rendered by QuickLaTeX.com P[\mathcal{S}_{n(x + t_p)}]\ \leq\ min_{x > 0}(1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^n](https://delfr.com/wp-content/ql-cache/quicklatex.com-0599fb0602e922319b50ca74d17e28b2_l3.png)
- Finally, for a given time interval of
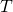 seconds, we can write:
seconds, we can write:
![Rendered by QuickLaTeX.com P[\mathcal{S}_T]\ \leq\ min_{x > 0}(1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^{\lfloor{\frac{T}{x+2t_p}}\rfloor}](https://delfr.com/wp-content/ql-cache/quicklatex.com-7cdc169c6c58b7ab726b623b15ae9482_l3.png)
Where
 denotes the floor function.
denotes the floor function.
The objective function of the previous optimization problem is not smooth due to the presence of the floor function. As a result, finding a closed form analytical solution might prove difficult. However, numerical methods could be employed to find the optimal upper bound. Observe that this upper bound decays exponentialy with ![]() and eventually converges to 0 when
and eventually converges to 0 when ![]() . We use the value of
. We use the value of ![]() that corresponds to the average block propagation delay to reach 99% of the network observed over a period of time extending from May
that corresponds to the average block propagation delay to reach 99% of the network observed over a period of time extending from May ![]() 2018 to August
2018 to August ![]() 2018 [2].
2018 [2].
Below, we include various graphs of this upper bound for different values of ![]() and for fixed
and for fixed ![]() and
and ![]()

These graphs show that for the pre-defined values of ![]() and
and ![]() the probability that a natural fork survives
the probability that a natural fork survives ![]() minutes (which on average corresponds to the addition of 2 new blocks on the blockchain) is upper-bounded by 0.25 (or almost 1 in 4 cases). When
minutes (which on average corresponds to the addition of 2 new blocks on the blockchain) is upper-bounded by 0.25 (or almost 1 in 4 cases). When ![]() minutes (i.e., the duration required to add an average of six new blocks on the blockchain), the upper bound goes down to 0.015 (or almost 1 in 67 cases). And when
minutes (i.e., the duration required to add an average of six new blocks on the blockchain), the upper bound goes down to 0.015 (or almost 1 in 67 cases). And when ![]() minutes, it goes down to 0.00022 (or almost 1 in 4500 cases).
minutes, it goes down to 0.00022 (or almost 1 in 4500 cases).
In the graphs above, we assumed a fixed block rate ![]() of 1 block per 10 minutes. This is the value used by Bitcoin. For what it is worth, one could further optimize the upper bound over positive values of
of 1 block per 10 minutes. This is the value used by Bitcoin. For what it is worth, one could further optimize the upper bound over positive values of ![]() For fixed
For fixed ![]() and
and ![]() the tightest upper bound becomes:
the tightest upper bound becomes:
![]()
In order to solve it, we first find the optimal value of ![]() that solves the following optimization problem:
that solves the following optimization problem:
![]()
Note that since the exponent appearing in the objective function does not depend on ![]() and since the base is a positive quantity, we can solve the following equivalent optimization problem whose objective function is now smooth:
and since the base is a positive quantity, we can solve the following equivalent optimization problem whose objective function is now smooth:
![]()
Note that when ![]() or when
or when ![]() the objective function tends to 1. The objective function turns out to be convex in
the objective function tends to 1. The objective function turns out to be convex in ![]() and we can solve for
and we can solve for ![]() by setting its first derivative with respect to
by setting its first derivative with respect to ![]() equal to 0. Doing so, yields:
equal to 0. Doing so, yields:
![]()
The tightest upper bound over all positive values of ![]() and
and ![]() then satisfies:
then satisfies:
![]()
For each of the following graph, we let ![]() and specify a particular value for
and specify a particular value for ![]() For each value of
For each value of ![]() we then calculate the corresponding
we then calculate the corresponding ![]() as outlined above, and plot the graph of
as outlined above, and plot the graph of
![]()
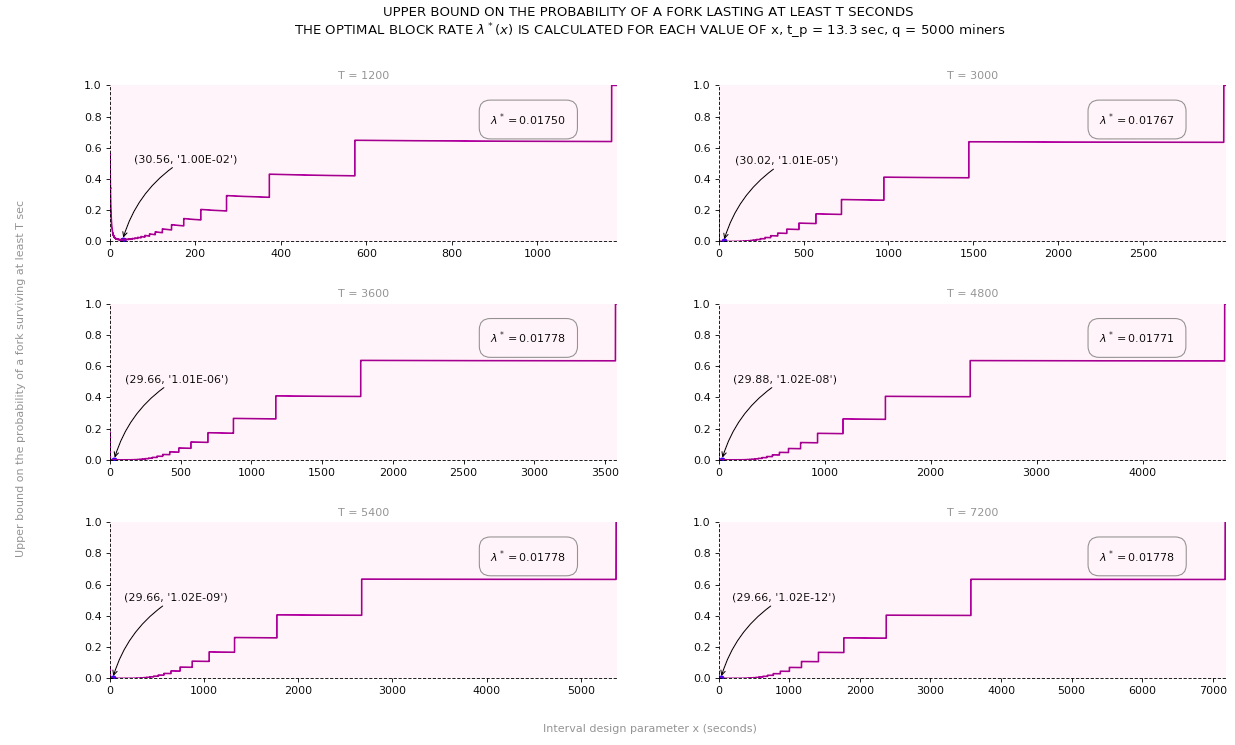
Objective #4: A non-trivial upper bound on the probability of a double-spend transaction coexisting with the legitimate transaction, ![]() seconds after the legitimate transaction is added to the blockchain:
seconds after the legitimate transaction is added to the blockchain:
The derivations above demonstrate that even if all miners were honest, forks are bound to happen, although they collapse with high likelihood after a finite time of their formation. The existence of natural forks could encourage dishonest customers to engage in double-spending behavior.
To see how, consider a scenario in which a customer spends some Satoshis to purchase a physical product. Let the transaction be denoted ![]() Suppose that at
Suppose that at ![]() the vendor sees his transaction
the vendor sees his transaction ![]() included in block #
included in block #![]() for the first time on the blockchain. Suppose that the customer issues another transaction
for the first time on the blockchain. Suppose that the customer issues another transaction ![]() (before or after
(before or after ![]() ) destined to himself and that uses the same UTXOs as
) destined to himself and that uses the same UTXOs as ![]() There is a chance that both
There is a chance that both ![]() and
and ![]() be selected by two different miners and included in two separate coexisting blocks. We define the following double-spending event:
be selected by two different miners and included in two separate coexisting blocks. We define the following double-spending event:
![]() “
“![]() and
and ![]() coexist on the bockchain,
coexist on the bockchain, ![]() seconds after
seconds after ![]() ‘s addition to the blockchain in block
‘s addition to the blockchain in block ![]() “
“
Note that if no fork is formed at or before block ![]() then
then ![]() will not constitute a double-spending risk since
will not constitute a double-spending risk since ![]() would have propagated to all nodes. As a result, a necessary condition for a double-spending risk to exist consists of the union of the following events:
would have propagated to all nodes. As a result, a necessary condition for a double-spending risk to exist consists of the union of the following events:
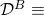 “A fork is formed at block #
“A fork is formed at block #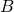 of the blockchain and
of the blockchain and 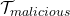 is added to this fork at some point in time. All miners shared a unified view of the blockchain right before #
is added to this fork at some point in time. All miners shared a unified view of the blockchain right before #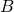 ‘s addition”
‘s addition”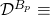 “A fork was formed at some block
“A fork was formed at some block 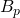 preceding
preceding  and
and 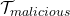 is added to this fork at some point in time. All miners shared a unified view of the blockchain right before #
is added to this fork at some point in time. All miners shared a unified view of the blockchain right before #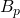 ‘s addition”
‘s addition”
We would like to calculate a non-trivial upper bound on ![]() We can write:
We can write:
![]()
-
![Rendered by QuickLaTeX.com P[\mathcal{DS}_T \cap \mathcal{D}^B] = P[\mathcal{DS}_T\ |\ \mathcal{D}^B] \times P[\mathcal{D}^B]](https://delfr.com/wp-content/ql-cache/quicklatex.com-66a6f0caf010429c00839441fe1d6515_l3.png)
We saw earlier that
![Rendered by QuickLaTeX.com P[\mathcal{D}^B] \leq 1 - e^{-q \lambda_{max} (\int_{0}^{\infty} g(t) dt)}.](https://delfr.com/wp-content/ql-cache/quicklatex.com-2ac83fc1efaf7ce03dc795cf9493d450_l3.png)
Moreover,
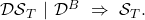 And so,
And so,![Rendered by QuickLaTeX.com P[\mathcal{DS}_T\ |\ \mathcal{D}^B] \leq\ min_{x > 0}(1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^{\lfloor{\frac{T}{x+2t_p}}\rfloor}](https://delfr.com/wp-content/ql-cache/quicklatex.com-49224dd02b421936485f93c1e9008c47_l3.png)
Assuming that
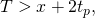 we get
we get![Rendered by QuickLaTeX.com P[\mathcal{DS}_T\ |\ \mathcal{D}^B] \leq\ min_{x > 0}(1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^{\frac{T}{x+2t_p}-1}](https://delfr.com/wp-content/ql-cache/quicklatex.com-af10ddb555356a6fbfbb6809bb08e185_l3.png)
- Let
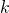 be a non-negative integer and let
be a non-negative integer and let 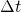 be an arbitrary interval of time. Without loss of generality, assume block
be an arbitrary interval of time. Without loss of generality, assume block  was added at
was added at 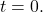 Define
Define 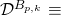 “Block #
“Block #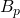 preceding #
preceding #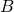 was created in interval
was created in interval ![Rendered by QuickLaTeX.com (-(k+1)\Delta t, -k \Delta t],](https://delfr.com/wp-content/ql-cache/quicklatex.com-b74eb03774f3b0ea0f583484ac7a7c9f_l3.png) a fork was formed at #
a fork was formed at #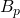 and
and 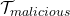 is added to this fork at some point in time. All miners shared a unified view of the blockchain right before #
is added to this fork at some point in time. All miners shared a unified view of the blockchain right before #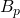 ‘s addition”. We can write:
‘s addition”. We can write:
![Rendered by QuickLaTeX.com P[\mathcal{DS}_T \cap \mathcal{D}^{B_p}] = lim_{\Delta t \rightarrow 0}\ \Sigma_{k=0}^{\infty}\ P[\mathcal{DS}_T \cap \mathcal{D}^{B_{p,k}}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-9eececabaaa73ef1e37e87cec84b8e0e_l3.png)
![Rendered by QuickLaTeX.com = lim_{\Delta t \rightarrow 0}\ \Sigma_{k=0}^{\infty}\ P[\mathcal{D}^{B_{p,k}}] \times P[\mathcal{DS}_T\ |\ \mathcal{D}^{B_{p,k}}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-1c554954be23e1f4ddcde1615ece168b_l3.png)
Note that
-
![Rendered by QuickLaTeX.com P[\mathcal{D}^{B_{p,k}}]\ =\ P[\mathcal{D}^{B_{p,k}}\ \cap\ \mathcal{D}^{B_p}]\ =\ P[\mathcal{D}^{B_{p}}] \times P[\mathcal{D}^{B_{p,k}}\ |\ \mathcal{D}^{B_{p}}].](https://delfr.com/wp-content/ql-cache/quicklatex.com-1704431f8d76d28bb9dcd3abceb83c68_l3.png)
-
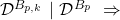 At least one block added in the interval
At least one block added in the interval ![Rendered by QuickLaTeX.com [-(k+1)\Delta t,\ -k \Delta t)].](https://delfr.com/wp-content/ql-cache/quicklatex.com-96159653f22d5c5d17944f50823da476_l3.png)
-

We then have:
![Rendered by QuickLaTeX.com P[\mathcal{D}^{B_{p,k}}] \leq P[\mathcal{D}^{B_p}] \times P[](https://delfr.com/wp-content/ql-cache/quicklatex.com-7038e46353f0bc95ba737599174ae554_l3.png) at least one block is added in interval
at least one block is added in interval ![Rendered by QuickLaTeX.com [-(k+1)\Delta t,\ -k \Delta t)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-6fcfb5c343e74a6db07fa9c30993fe54_l3.png)
As a result,
![Rendered by QuickLaTeX.com P[\mathcal{DS}_T \cap \mathcal{D}^{B_p}]\ \leq lim_{\Delta t \rightarrow 0}\ \{P[\mathcal{D}^{B_p}] \times](https://delfr.com/wp-content/ql-cache/quicklatex.com-524e63e6365bbf09035fc44d8f13dce7_l3.png)
![Rendered by QuickLaTeX.com (1-e^{-\lambda \Delta t})\ \Sigma_{k=0}^{\infty}\ min_{x > 0}(1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^{\lfloor{\frac{T + k \Delta t}{x+2t_p}}\rfloor}\}](https://delfr.com/wp-content/ql-cache/quicklatex.com-468eec37198e4aab75ef1cb46acc67ad_l3.png)
Assuming
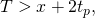 we get
we get ![Rendered by QuickLaTeX.com P[\mathcal{DS}_T \cap \mathcal{D}^{B_p}] \leq](https://delfr.com/wp-content/ql-cache/quicklatex.com-59ed56879a77d136b5ca6da5e60ab82b_l3.png)
![Rendered by QuickLaTeX.com lim_{\Delta t \rightarrow 0}\ \{P[\mathcal{D}^{B_p}] \times](https://delfr.com/wp-content/ql-cache/quicklatex.com-53c23e1bd380fc7407ce71f923a82602_l3.png)
![Rendered by QuickLaTeX.com (1-e^{-\lambda \Delta t})\ \Sigma_{k=0}^{\infty}\ min_{x > 0}(1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^{\frac{T + k \Delta t}{x+2t_p} - 1}\}](https://delfr.com/wp-content/ql-cache/quicklatex.com-c1546801676857414e1142f54d86ba0c_l3.png)
In the limit when
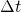 becomes infinitesimally small and tends to
becomes infinitesimally small and tends to 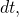 the quantity
the quantity 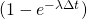 tends to
tends to 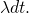 We can then write
We can then write![Rendered by QuickLaTeX.com P[\mathcal{DS}_T \cap \mathcal{D}^{B_p}] \leq P[\mathcal{D}^{B_p}]\ min_{x > 0} \int_0^{\infty} \lambda (1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^{\frac{T + t}{x+2t_p} - 1} dt](https://delfr.com/wp-content/ql-cache/quicklatex.com-71daf6412b3de67b0698c24a89121292_l3.png)
![Rendered by QuickLaTeX.com =P[\mathcal{D}^{B_p}]\ min_{x > 0}\ \frac{-\lambda (x + 2t_p)}{ln(1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])} (1 - q e^{-\lambda (x + 2t_p)}[e^{(\lambda x) / q} - 1])^{\frac{T}{x+2t_p} - 1}](https://delfr.com/wp-content/ql-cache/quicklatex.com-fa0884b5726ae7d5ec072730f220de42_l3.png)
Similar to
![Rendered by QuickLaTeX.com P[\mathcal{D}^{B}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-945ee4e4d77b0314a477844fd6da42b4_l3.png) , we have
, we have![Rendered by QuickLaTeX.com P[\mathcal{D}^{B_p}] \leq 1 - e^{-q \lambda_{max} (\int_{0}^{\infty} g(t) dt)}.](https://delfr.com/wp-content/ql-cache/quicklatex.com-0ce6b068523333ca22279802895b2419_l3.png)
-
We then conclude that ![]()
![]()
![]()
The graphs below depict the upper bound on the probability that a double spend transaction ![]() coexists with
coexists with ![]() on the blockchain
on the blockchain ![]() seconds after
seconds after ![]() is added to block #
is added to block #![]() for various values of
for various values of ![]() and
and ![]()
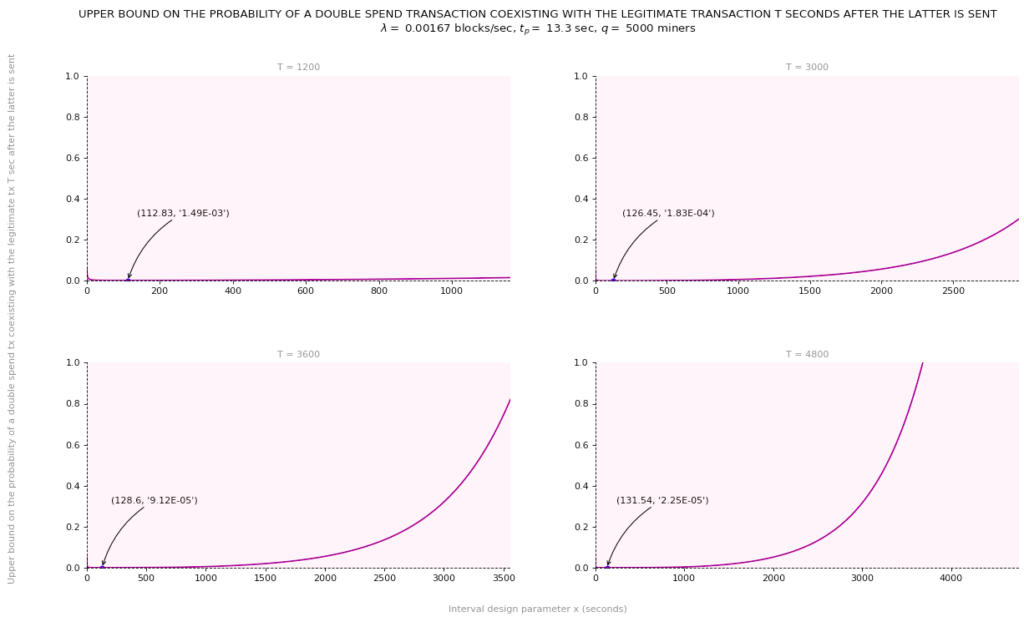
The above graphs show that if before handing over the goods, the vendor waits for an additional ![]() minutes after he sees
minutes after he sees ![]() added to block #
added to block #![]() on the blockchain (which at a block rate of
on the blockchain (which at a block rate of ![]() would roughly correspond to two additional blocks on top of #
would roughly correspond to two additional blocks on top of #![]() ), then for
), then for ![]()
![]() and all miners being honest and sharing the same hash rate, the probability of a double-spend attempt coexisting with
and all miners being honest and sharing the same hash rate, the probability of a double-spend attempt coexisting with ![]() at time
at time ![]() is upper-bounded by 0.00149.
is upper-bounded by 0.00149.
That means that there is at most a probability of 0.00149 that ![]() is still part of a parallel fork. By virtue of being sustained, it could still become part of the longest chain. If this happens,
is still part of a parallel fork. By virtue of being sustained, it could still become part of the longest chain. If this happens, ![]() gets thrown back into the mempool and
gets thrown back into the mempool and ![]() gets validated instead. On the other hand, waiting for an an additional
gets validated instead. On the other hand, waiting for an an additional ![]() minutes (i.e., roughly 5 additional blocks on top of #
minutes (i.e., roughly 5 additional blocks on top of #![]() ), would bring down this probability to 0.000183.
), would bring down this probability to 0.000183.
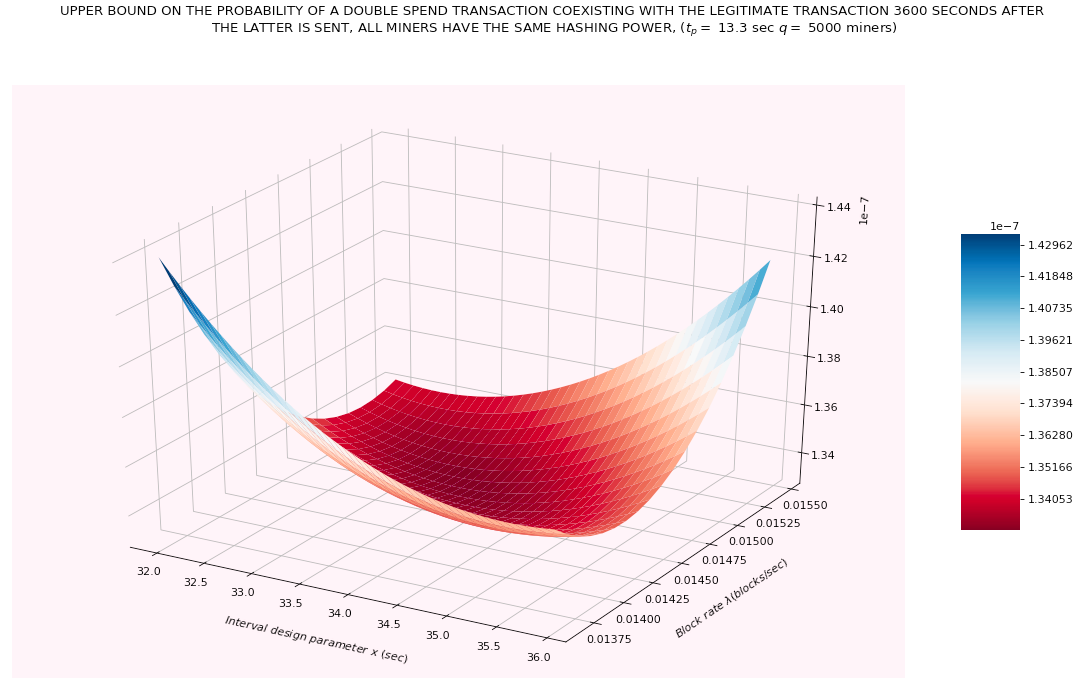
One could also optimize the upper bound not only over ![]() but also over
but also over ![]() Below is a plot showing the optimal value for the case
Below is a plot showing the optimal value for the case ![]() minutes. In this case, the tightest upper bound is 1.33
minutes. In this case, the tightest upper bound is 1.33 ![]() which is achieved for
which is achieved for ![]() blocks / sec and
blocks / sec and ![]() sec.
sec.
A small note on the value of ![]() To the extent of our knowledge, the choice of
To the extent of our knowledge, the choice of ![]() used in Bitcoin is not the result of a pure mathematical optimization exercise. The larger the value of
used in Bitcoin is not the result of a pure mathematical optimization exercise. The larger the value of ![]() the higher the probability of a natural fork occuring. Natural forks are not desirable as they possibly pave the way to double-spending attempts. However, this is not the only metric that counts.
the higher the probability of a natural fork occuring. Natural forks are not desirable as they possibly pave the way to double-spending attempts. However, this is not the only metric that counts.
Another important consideration has to do with the storage capacity requirement and the rate of growth of such capacity that needs to be maintained at the level of each full node on the network. A higher ![]() means faster transaction processing but also faster growth of ever-increasing storage requirement. It is most likely that only a handful of nodes will be able to afford such storage, subsequently leading to a centralization scenario. This stands in sharp contrast with Bitcoin’s fundamental philosophy. As a result of this tradeoff, Satoshi’s choice of
means faster transaction processing but also faster growth of ever-increasing storage requirement. It is most likely that only a handful of nodes will be able to afford such storage, subsequently leading to a centralization scenario. This stands in sharp contrast with Bitcoin’s fundamental philosophy. As a result of this tradeoff, Satoshi’s choice of ![]() is probably a good compromise.
is probably a good compromise.
3. Probability that dishonest miner(s) succeed in creating a dominant fork: 51% attack
In this section we look at the second type of imperfections alluded to earlier. More specifically, we turn to the possibility that a subset of dishonest miner(s) decide to disregard the PoW consensus protocol and mine on top of a parallel chain different than the one with the highest amount of cumulative work.
This type of behavior has been introduced and analyzed in section 11 of Nakamoto’s seminal paper [3]. The analysis demonstrates that dishonnest miner(s) could possibly generate a parallel chain that overtakes the original honest chain. As a consequence, malicious miner(s) can potentially engage in double spending behavior.
Such a scenario is commonly referred to as a 51% attack, although malicious miner(s) do not necessarily need 51% of the total hashing power of the network to launch a double spending attack. A control of 51% or more of the total hashing power will however guarantee that the attack will be successful. On the other hand, control of less than 51% is not associated with a deterministic state of success, but rather a probabilistic one. The analysis in [3] quantifies the probability of success as a function of said control. In this section, we simply clarify the mathematical foundation of this analysis.
Building on the notation used in section 2, we further define the following quantities:
- Let
 be the subset of malicious miner(s) staging a 51% attack.
be the subset of malicious miner(s) staging a 51% attack. - Let
 denote the fraction of the total hashing power controlled by the malicious miner(s). Note that in [3], this quantity is denoted by
denote the fraction of the total hashing power controlled by the malicious miner(s). Note that in [3], this quantity is denoted by 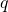 (in our notation,
(in our notation, 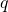 refers to the total number of miners).
refers to the total number of miners). - Let
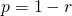 denote the fraction of the total hashing power controlled by the honest miners.
denote the fraction of the total hashing power controlled by the honest miners. - Let
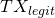 correspond to the legitimate transaction against which
correspond to the legitimate transaction against which  will stage a 51% attack, and let
will stage a 51% attack, and let  be the block to which
be the block to which 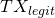 was initially added.
was initially added. - Let
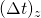 denote the interval of time extending from the moment
denote the interval of time extending from the moment 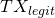 was added to
was added to  to the time the
to the time the 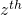 subsequent block following
subsequent block following  got added to the honest chain.
got added to the honest chain.
We also define the following two events:
 “The subset of malicious miner(s) with a fraction
“The subset of malicious miner(s) with a fraction  of the network’s total hashing power conduct a successful 51% attack on
of the network’s total hashing power conduct a successful 51% attack on 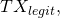 and
and 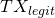 has been previously validated by the addition of
has been previously validated by the addition of  blocks on top of
blocks on top of  on the honest chain.”
on the honest chain.”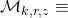 “The subset of malicious miner(s) with a fraction
“The subset of malicious miner(s) with a fraction  of the network’s total hashing power created and added
of the network’s total hashing power created and added 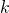 blocks to the parallel chain in interval
blocks to the parallel chain in interval 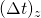 .”
.”
We can write:
![]()
Calculating ![]() : Given a network block rate of
: Given a network block rate of ![]() blocks/sec, the rate associated with honest miners is
blocks/sec, the rate associated with honest miners is ![]() blocks/sec, and that associated with malicious miner(s) is
blocks/sec, and that associated with malicious miner(s) is ![]() blocks/sec. As a result,
blocks/sec. As a result, ![]() sec. In this interval, the subset of malicious miner(s) generate an average of
sec. In this interval, the subset of malicious miner(s) generate an average of ![]() blocks. As a result, we can model malicious miner(s) block generation over this inteval as a Poisson process with mean
blocks. As a result, we can model malicious miner(s) block generation over this inteval as a Poisson process with mean ![]() blocks. We get:
blocks. We get:
![]()
Calculating ![]() : Knowing that in interval
: Knowing that in interval ![]() the malicious miner(s) generated
the malicious miner(s) generated ![]() blocks on the parallel chain, we need to calculate the probability that the malicious miner(s) catch-up to the honest chain and generate a parallel chain that is at least as long (note that technically speaking, the parallel chain should be one block longer than the honest chain for the attack to be successful, but Nakamoto’s analysis considers the case of equal length instead). Clearly, if
blocks on the parallel chain, we need to calculate the probability that the malicious miner(s) catch-up to the honest chain and generate a parallel chain that is at least as long (note that technically speaking, the parallel chain should be one block longer than the honest chain for the attack to be successful, but Nakamoto’s analysis considers the case of equal length instead). Clearly, if ![]() the probability is 1. When
the probability is 1. When ![]() we can model the process as a binomial random walk whereby given that the malicious miner(s)’s parallel chain is
we can model the process as a binomial random walk whereby given that the malicious miner(s)’s parallel chain is ![]() blocks shorter than the honest chain:
blocks shorter than the honest chain:
- Every time the malicious miner(s) generate a new block, the gap gets reduced by 1.
- Every time the honest miners generate a new block, the gap gets increased by 1.
- Otherwise, the gap remains the same.
This problem turns out ot be a slight variant of the Gambler’s Ruin Problem that we introduce next.
- The Gambler’s Ruin Problem:
- The setting consists of a gambler who initially has
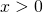 units of currency (UOC for short).
units of currency (UOC for short). - The gambler engages in a series of bets whereby every time she wins she gets UOC
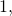 and every time she loses, she gives UOC
and every time she loses, she gives UOC 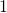 .
. - Suppose that the gambler has a probability
 of winning each bet and a probability
of winning each bet and a probability 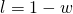 of losing. All bets are mutually independent.
of losing. All bets are mutually independent. - The objective is for the gambler to reach a fortune of UOC
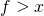 before losing all her capital. As a result, the process will stop if either the gambler accumulates UOC
before losing all her capital. As a result, the process will stop if either the gambler accumulates UOC  or if she sees her capital reduced to 0.
or if she sees her capital reduced to 0.
In what follows, we calculate the probability that the gambler wins knowing that she started the game with UOC
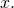 This is the probability that she reaches a fortune of UOC
This is the probability that she reaches a fortune of UOC  at some point in time knowing that she started off with UOC
at some point in time knowing that she started off with UOC 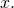 We denote it by
We denote it by 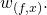 A similar derivation can be found in [5] and [4]. Note that in this version of the game, the gambler cannot play if she does not have a positive amount of capital to start the betting process with. This stands in contrast to the aforementioned situation where malicious miner(s) start off with a block deficit. Later on, we will account for this variation.
A similar derivation can be found in [5] and [4]. Note that in this version of the game, the gambler cannot play if she does not have a positive amount of capital to start the betting process with. This stands in contrast to the aforementioned situation where malicious miner(s) start off with a block deficit. Later on, we will account for this variation.We start by defining the following events:
{
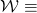 “The gambler wins”
“The gambler wins”{
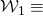 “The gambler wins the first bet in the series”
“The gambler wins the first bet in the series”{
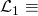 “The gambler looses the first bet in the series”
“The gambler looses the first bet in the series”And let
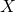 be a random variable denoting the amount of capital held by the gambler at the beginning of the game.
be a random variable denoting the amount of capital held by the gambler at the beginning of the game.We can write:
![Rendered by QuickLaTeX.com P[\mathcal{W}\ |\ X=x] = P[\mathcal{W} \cap \mathcal{W}_1\ |\ X=x] + P[\mathcal{W} \cap \mathcal{L}_1\ |\ X=x]](https://delfr.com/wp-content/ql-cache/quicklatex.com-301ad464dc3101ede758ed48754ba2c3_l3.png)
![Rendered by QuickLaTeX.com = P[\mathcal{W}\ |\ X=x,\ \mathcal{W}_1] \times P[\mathcal{W}_1\ |\ X=x] +](https://delfr.com/wp-content/ql-cache/quicklatex.com-0c1e92030737442425300c4c733fbd6b_l3.png)
![Rendered by QuickLaTeX.com P[\mathcal{W}\ |\ X=x,\ \mathcal{L}_1] \times P[\mathcal{L}_1\ |\ X=x]](https://delfr.com/wp-content/ql-cache/quicklatex.com-3bf0e6b21e9a1d8cf13981aa2d327373_l3.png)
![Rendered by QuickLaTeX.com = P[\mathcal{W}\ |\ X = x+1] \times P[\mathcal{W}_1\ |\ X=x]](https://delfr.com/wp-content/ql-cache/quicklatex.com-bb46f73f5b09b6490f81d3319c963bdf_l3.png)
![Rendered by QuickLaTeX.com + P[\mathcal{W}\ |\ X=x-1] \times P[\mathcal{L}_1\ |\ X=x]](https://delfr.com/wp-content/ql-cache/quicklatex.com-f0cb65a0bcac766e56dc70f09289cd2d_l3.png)
In other terms, we have:
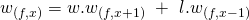
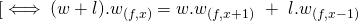
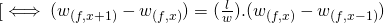
 since
since 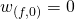
Recognizing a telescoping series structure, we write:
![Rendered by QuickLaTeX.com w_{(f, x+1)} - w_{(f, 1)} = \Sigma_{j=1}^x (w_{(f, j+1)} - w_{(f, j)}) = [\Sigma_{j=1}^x (\frac{l}{w})^j].\ w_{(f, 1)}](https://delfr.com/wp-content/ql-cache/quicklatex.com-214b413f3d98ddab86744a57b7b7eb55_l3.png)
And so,
![Rendered by QuickLaTeX.com w_{(f, x)} = [\Sigma_{j=0}^{x-1} (\frac{l}{w})^j].\ w_{(f, 1)} =](https://delfr.com/wp-content/ql-cache/quicklatex.com-58ce33c41f4b4610111ea90a1113bd54_l3.png)
![Rendered by QuickLaTeX.com [\frac{1 - (\frac{l}{w})^{x}}{1 - \frac{l}{w}}].\ w_{(f, 1)},](https://delfr.com/wp-content/ql-cache/quicklatex.com-d20677ccea1401ebd863f65ea591a212_l3.png) if
if 
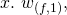 if
if 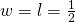
Noting that
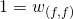 and applying the above when
and applying the above when 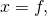 we get
we get![Rendered by QuickLaTeX.com 1 = [\frac{1 - (\frac{l}{w})^{f}}{1 - \frac{l}{w}}].\ w_{(f, 1)}\ ,](https://delfr.com/wp-content/ql-cache/quicklatex.com-a9c380e8d085b2bc8c59680cdd5e348f_l3.png) if
if 
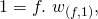 if
if 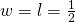
Which then allows us to conclude that

![Rendered by QuickLaTeX.com [\frac{1 - \frac{l}{w}}{1 - (\frac{l}{w})^{f}}],\](https://delfr.com/wp-content/ql-cache/quicklatex.com-a18250b5b1bf6e405a2e35263f12f82b_l3.png) if
if 
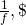 if
if 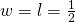
Putting it altogether, we get
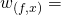
![Rendered by QuickLaTeX.com \frac{1 - (\frac{l}{w})^{x}}{1 - (\frac{l}{w})^{f}}],](https://delfr.com/wp-content/ql-cache/quicklatex.com-4b06f29e7da228fc4094a46ad2ac3a88_l3.png) if
if 
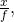 if
if 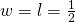
- The setting consists of a gambler who initially has
- Adapting the Gambler’s Ruin Problem to the case of a 51% attack: In the context of a 51% attack, and for

![Rendered by QuickLaTeX.com P[\mathcal{A}^{51}_{r,z}\ | \mathcal{M}_{k,r,z}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-022b1e209bce24e73db866165b957b38_l3.png) is the probability that the subset of malicious miner(s) catch up to the honest chain when the malicious miner(s)’ parallel chain is
is the probability that the subset of malicious miner(s) catch up to the honest chain when the malicious miner(s)’ parallel chain is 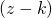 blocks behind. In other terms, the malicious miner(s) have a deficit of
blocks behind. In other terms, the malicious miner(s) have a deficit of 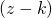 blocks at the beginning of the process and we are interested in calculating the probability that they catch-up at some point in time.
blocks at the beginning of the process and we are interested in calculating the probability that they catch-up at some point in time.
Note that under this setting, the block deficit may widen without having any lower-bound constraint.In the setting of the Gambler’s Ruin Problem, the gambler cannot play when she is in a deficit and will have to stop as soon as her betting capital reaches 0. As such, the problem must be modified to account for a scenario where the gambler could borrow unlimited credit if need be, to continue playing the game.
An equivalent formulation consists of a gambler having an infinite amount of capital to start with. Formally, we assume the same setting as the original problem. The gambler however, has a deficit of UOC
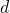 . She then borrows UOC
. She then borrows UOC  and starts the game with the objective of reaching UOC
and starts the game with the objective of reaching UOC  where
where 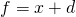 . If she wins, she returns UOC
. If she wins, she returns UOC 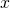 to her creditor and keeps UOC
to her creditor and keeps UOC 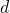 so as to break-even. In case she loses, she does not return anything to her creditor.
so as to break-even. In case she loses, she does not return anything to her creditor.Clearly, the above setting is unrealistic due to the dearth of extremely benevolent creditors. However, when we are dealing with a deficit of a block nature rather than a monetary one, this setting becomes acceptable. We then let
 and compute the corresponding probability of success. In our block deficit case,
and compute the corresponding probability of success. In our block deficit case, 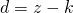 blocks.
blocks.We get
![Rendered by QuickLaTeX.com lim_{x \rightarrow \infty}\ [w_{(x+(z-k),\ x)}] =](https://delfr.com/wp-content/ql-cache/quicklatex.com-3f3845c2dc4ef82ded00202ffd0ec597_l3.png)
![Rendered by QuickLaTeX.com lim_{x \rightarrow \infty}\ [\frac{1 - (\frac{l}{w})^{x}}{1 - (\frac{l}{w})^{x+(z-k)}}],](https://delfr.com/wp-content/ql-cache/quicklatex.com-c1825720dd49187ac7e87301f58d74b0_l3.png) if
if 
![Rendered by QuickLaTeX.com lim_{x \rightarrow \infty}\ [\frac{x}{x+(z-k)}],](https://delfr.com/wp-content/ql-cache/quicklatex.com-f55c7599bbaecab65f6096071ddd7c58_l3.png) if
if 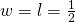
Next, note that if
 then
then 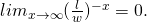 And so
And so![Rendered by QuickLaTeX.com lim_{x \rightarrow \infty}\ [\frac{1 - (\frac{l}{w})^{x}}{1 - (\frac{l}{w})^{x+(z-k)}}] = lim_{x \rightarrow \infty}\ [\frac{(\frac{l}{w})^{-x} - 1}{(\frac{l}{w})^{-x} - (\frac{l}{w})^{(z-k)}}] = (\frac{w}{l})^{(z-k)}](https://delfr.com/wp-content/ql-cache/quicklatex.com-2745b3cdc40830e8a2f07d40f1123148_l3.png)
And if
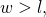 then
then 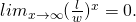 And so
And so![Rendered by QuickLaTeX.com lim_{x \rightarrow \infty}\ [\frac{1 - (\frac{l}{w})^{x}}{1 - (\frac{l}{w})^{x+(z-k)}}] = 1](https://delfr.com/wp-content/ql-cache/quicklatex.com-437cd0c80696dd95248a127fe08e0e7f_l3.png)
Finally, if
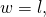 then
then ![Rendered by QuickLaTeX.com lim_{x \rightarrow \infty}\ [\frac{x}{x+(z-k)}] = 1.](https://delfr.com/wp-content/ql-cache/quicklatex.com-ec5a88f052fdf27fdf2c4d066ce163e3_l3.png)
As a result,
![Rendered by QuickLaTeX.com lim_{x \rightarrow \infty}\ [w_{(x+(z-k),\ x)}] = (\frac{w}{l})^{(z-k)}](https://delfr.com/wp-content/ql-cache/quicklatex.com-bb114eb9b1e4b206fe0ca4cad01d236c_l3.png) if
if  and
and 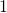 if
if 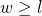
If malicious miner(s) are not incurring a block deficit, i.e.,
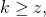 then
then![Rendered by QuickLaTeX.com P[\mathcal{A}^{51}_{r,z}\ | \mathcal{M}_{k,r,z}] = 1](https://delfr.com/wp-content/ql-cache/quicklatex.com-189ffb701378b1dd8008d3336303c702_l3.png)
Otherwise, if
 then noting that the probability of malicious miner(s) finding the next block is equal to
then noting that the probability of malicious miner(s) finding the next block is equal to  and the one corresponding to the honest miners is equal to
and the one corresponding to the honest miners is equal to 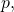 we get:
we get:![Rendered by QuickLaTeX.com P[\mathcal{A}^{51}_{r,z}\ | \mathcal{M}_{k,r,z}] = (\frac{r}{p})^{(z-k)}](https://delfr.com/wp-content/ql-cache/quicklatex.com-131dfd32db25035dd72fa4101f768ad7_l3.png) if
if  and
and 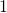 if
if 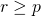
The calculations above allow us to conclude that:
![]()
![]()
![]() if
if ![]()
and ![]() if
if ![]()
In the graphs below we plot the probability of a successful 51% attack as a function of the fraction ![]() of the total hashing power controlled by the subset of malicious miner(s). We do so for different values of the block validation height
of the total hashing power controlled by the subset of malicious miner(s). We do so for different values of the block validation height ![]()
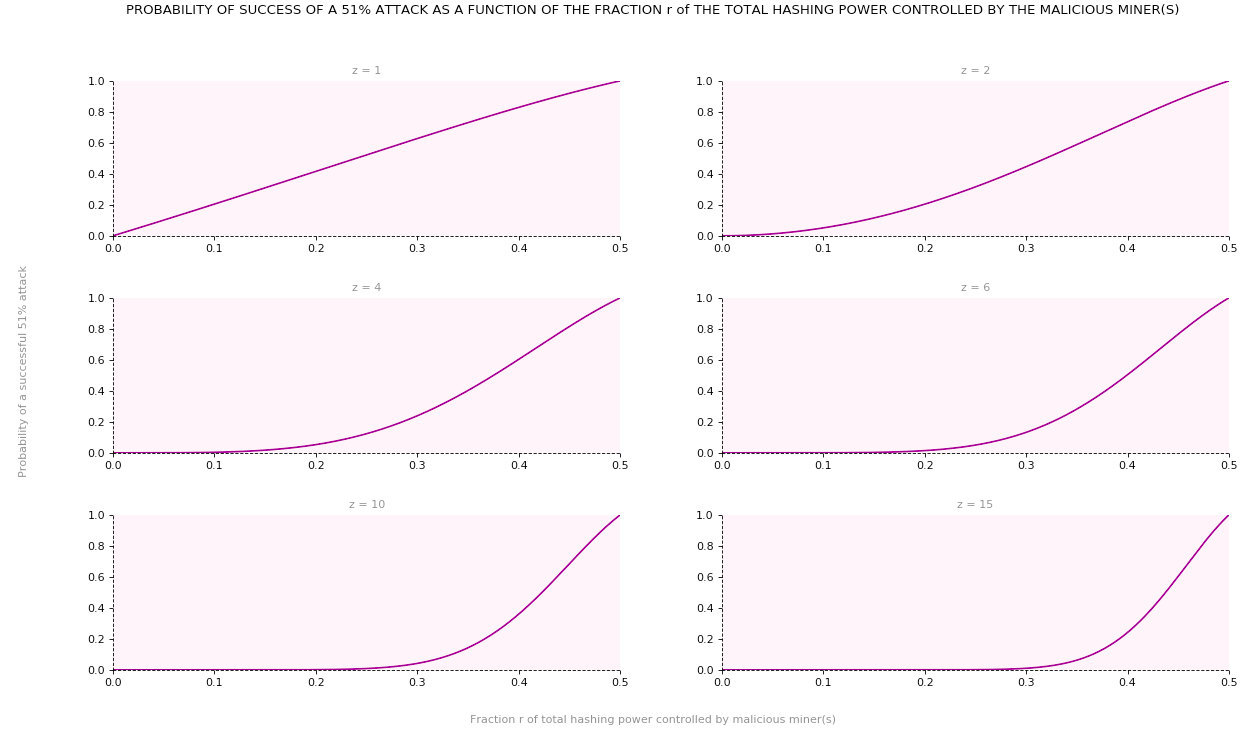
For example, assuming that malicious miner(s) controlled 15% of the total hashing power of the network (i.e., ![]() ), then a block validation height of 6 blocks (i.e.,
), then a block validation height of 6 blocks (i.e., ![]() ) is associated with a probability of a successful attack of 0.268%.
) is associated with a probability of a successful attack of 0.268%.
4. References
[1] Christian Decker and Roger Wattenhofer. Information propagation in the bitcoin network, 2013.
[2] DSN. Block propagation delay history.
[3] Satoshi Nakamoto. Bitcoin: A peer-to-peer electronic cash system. White Paper, 2008.
[4] A. Pinar Ozisik and Brian Neil Levine. An explanation of nakamoto’s analysis of double-spend attacks, online, 2017.
[5] Karl Sigman. Gambler’s ruin problem, online, 2016.
Tags: 51%, attack, blockchain, double spend, fork, miner

No comments
Comments feed for this article
Trackback link: https://delfr.com/blockchain-fork-analysis/trackback/