1. Introduction
The purpose of this note is to provide an introduction to the Generalized Linear Model and a matricial formulation of statistical learning derived from the class of exponential distributions with dispersion parameter. We assume that the reader is comfortable with linear algebra and multivariable calculus, has an understanding of basic probability theory and is familiar with supervised learning concepts.
A number of regression and classification models commonly used in supervised learning settings turn out to be specific cases derived from the family of exponential distributions. This note is organized as follows:
- Section 2 describes the family of exponential distributions and their associated Generalized Linear Model. The family described in [3] counts a significant number of distributions including e.g., the univariate Gaussian, Bernoulli, Poisson, Geometric, and Multinomial cases. Other distributions such as the multivariate Gaussian lend themselves to a natural generalization of this model. In order to do so, we extend the family of exponential distributions with dispersion parameter [3] to include symmetric positive definite dispersion matrices.
- Section 3 derives the Generalized Linear Model Cost Function and its corresponding Gradient and Hessian all expressed in component form. We derive the expressions associated with the general case that includes a dispersion matrix. We also derive simplified versions for the specific case when the dispersion matrix is a positive scalar multiple of the identity matrix.
- In Section 4, we limit ourselves to distributions whose dispersion matrix is a positive scalar multiple of the identity matrix. These are precisely the ones described in [3]. We express their associated Cost Function, Gradient and Hessian using concise matrix notation. We will separately analyze the case of the multivariate Gaussian distribution and derive its associated Cost Function and Gradient in matrix form in section 7.
- Section 5 provides a matricial formulation of three numerical algorithms that can be used to minimize the Cost Function. They include the Batch Gradient Descent (BGD), Stochastic Gradient Descent (SGD) and Newton Raphson (NR) methods.
- Section 6 applies the matricial formulation to a select set of exponential distributions whose dispersion matrix is a positive scalar multiple of the identity. In particular, we consider the following:
- Univariate Gaussian distribution (which yields linear regression).
- Bernoulli distribution (which yields logistic regression).
- Poisson distribution.
- Geometric distribution.
- Multinomial distribution (which yields softmax regression).
- Section 7 treats the case of the multivariate Gaussian distribution. It is an example of an exponential distribution with dispersion matrix that is not necessarily a positive scalar multiple of the identity matrix. In this case, the dispersion matrix turns out to be the precision matrix which is the inverse of the covariance matrix. We derive the corresponding Cost Function in component form and also express it using matrix notation. We then derive the Cost function’s Gradient, express it in matrix notation and show how to to minimize the Cost Function using BGD. We finally consider the specific case of a non-weighted Cost Function without regularization and derive a closed-form solution for the optimal values of its minimizing parameters.
- Section 8 provides a python script that implements the Generalized Linear Model Supervised Learning class using the matrix notation. We limit ourselves to cases where the dispersion matrix is a positive scalar multiple of the identity matrix. The code provided is meant for educational purposes and we recommend relying on existing and tested packages (e.g., scikit-learn) to run specific predictive models.
2. Generalized Linear Model
Discriminative supervised learning models: Loosely speaking, a supervised learning model is an algorithm that when fed a training set (i.e., a set of inputs and their corresponding outputs) derives an optimal function that can make “good” output predictions when given new, previously unseen inputs.
More formally, let ![]() an
an ![]() denote the input and output spaces respectively. Let
denote the input and output spaces respectively. Let
![]() x
x ![]()
denote a given training set for a finite positive integer ![]() The supervised learning algorithm will output a function
The supervised learning algorithm will output a function ![]() that optimizes a certain performance metric usually expressed in the form of a Cost Function. The function
that optimizes a certain performance metric usually expressed in the form of a Cost Function. The function ![]() can then be applied to an input
can then be applied to an input ![]() to predict its corresponding output
to predict its corresponding output ![]() . Whenever
. Whenever ![]() is limited to a discrete set of values, we refer to the learning problem as a classification. Otherwise, we call it a regression.
is limited to a discrete set of values, we refer to the learning problem as a classification. Otherwise, we call it a regression.
The exercise of conducting predictions in a deterministic world is futile. Inject that world with a dose of randomness and that exercise becomes worthwhile. In order to model randomness, we usually lean on probabilistic descriptions of the distribution of relevant variables. More specifically, we may assume certain distributions on the set of inputs, the set of outputs, or joint distributions on inputs and outputs taken together. For the purpose of this note, we limit ourselves to models that make assumptions on the distribution of the output given the input, without giving any consideration to the underlying distribution of the inputs themselves. Such models are referred to as discriminative learning models.
Generalized Linear model: In essence, a Generalized Linear Model consists of three elements.
#1: A random component modeled as an instance from a family of probability distributions of the form:
(1) ![]()
Modulo variables and maps naming, this family of distributions corresponds to the one introduced in [3]. It is defined for positive dispersion parameters ![]() We now introduce a more general version where the dispersion parameter
We now introduce a more general version where the dispersion parameter ![]() could be a symmetric positive definite matrix
could be a symmetric positive definite matrix ![]() . We define the enlarged family of exponential distributions to include those of the following form:
. We define the enlarged family of exponential distributions to include those of the following form:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed { \begin{gathered} p(y;\ \eta, \Lambda)\ =\ b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ -\ [q(\eta)]^{T}\ \Lambda\ q(\eta)\ ]} \\ \equiv\ b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ -\ c(\eta, \Lambda)\ ]} \end{gathered} } \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-483bc988d1f0f7ede841871b492bf63d_l3.png)
where we define ![]() to be equal to
to be equal to ![]() The maps and parameters appearing in the expression above are described as follows:
The maps and parameters appearing in the expression above are described as follows:
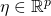 is known as the natural parameter vector. We will soon impose a relationship between the input
is known as the natural parameter vector. We will soon impose a relationship between the input 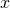 and
and 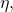 which will link the input to the output
which will link the input to the output 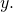
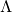 is a symmetric element of
is a symmetric element of 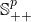 (i.e., a
(i.e., a 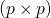 symmetric positive-definite matrix). We refer to it as the dispersion parameter matrix.
symmetric positive-definite matrix). We refer to it as the dispersion parameter matrix.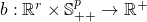 is known as the non-negative base measure. It maps
is known as the non-negative base measure. It maps 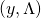 to the positive scalar value
to the positive scalar value 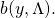
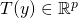 is a sufficient statistic of
is a sufficient statistic of 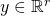 and has the same dimension as
and has the same dimension as 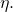 For all practical purposes, this means that the probability of a random variable taking on a particular value when conditioned on
For all practical purposes, this means that the probability of a random variable taking on a particular value when conditioned on 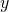 is equal to the probability of it taking the same value when conditioned on
is equal to the probability of it taking the same value when conditioned on 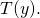 In other terms, whatever can be learned by conditioning on
In other terms, whatever can be learned by conditioning on 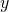 can also be learned by conditioning on
can also be learned by conditioning on 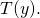
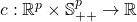 is known as the log-partition function. It maps
is known as the log-partition function. It maps 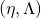 to
to ![Rendered by QuickLaTeX.com c(\eta, \Lambda) = [q(\eta)]^{T}\ \Lambda\ q(\eta),](https://delfr.com/wp-content/ql-cache/quicklatex.com-d6c28d886b9126f45c647d4396b7cc12_l3.png) where
where 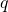 is a vector-valued map from
is a vector-valued map from 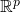 into
into 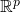 that depends only on
that depends only on 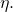 We denote the components of the column vector
We denote the components of the column vector 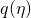 by
by ![Rendered by QuickLaTeX.com [q_{1}(\eta)\ ..\ q_{p}(\eta)]^{T},](https://delfr.com/wp-content/ql-cache/quicklatex.com-de89c193a8f0aba55e824b2e9aed5101_l3.png) where each
where each 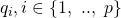 is a map from
is a map from 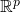 into
into 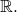
The rationale for the log-partition nomenclature stems from it being chosen to ensure that
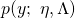 integrates to 1. Doing so allows us to express
integrates to 1. Doing so allows us to express 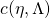 as a function of the other parameters:
as a function of the other parameters: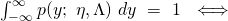
![Rendered by QuickLaTeX.com \int^{\infty}_{-\infty} b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ -\ c(\eta, \Lambda)\ ]}\ dy\ =\ 1\ \iff](https://delfr.com/wp-content/ql-cache/quicklatex.com-13496fa65fe8ece344cdf1166074b164_l3.png)
![Rendered by QuickLaTeX.com ln\ \{{\ \int^{\infty}_{-\infty} b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ -\ c(\eta, \Lambda)\ ]}\ dy\ \}}\ =\ 0\ \iff](https://delfr.com/wp-content/ql-cache/quicklatex.com-edbe471d80d6ad3f851249a6431b7bfa_l3.png)
![Rendered by QuickLaTeX.com ln\ (\ e^{-c(\eta, \Lambda)}\ )\ +\ ln\ \{{\ \int^{\infty}_{-\infty} b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ ]}\ dy\ \}}\ =\ 0\ \iff](https://delfr.com/wp-content/ql-cache/quicklatex.com-0d19e0677aca219e4d4cbe232a1170aa_l3.png)
(3)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed{c(\eta, \Lambda) = ln\ \{{\ \int^{\infty}_{-\infty} b(y, \Lambda)\ e^{[\ \eta^{T} \Lambda\ T(y)\ ]}\ dy\ \}}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-d2bf809650b911ac91470dedb57cc1fb_l3.png)
In what follows, we derive expressions for the log-partition function’s Gradient and Hessian
The log-partition function’s Gradient: We start by defining the one-form Gradient of
 with respect to
with respect to 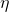 to be the quantity:
to be the quantity:![Rendered by QuickLaTeX.com (\bigtriangledown_{\eta}\ c)\ \equiv\ [\ \frac{\partial c}{\partial \eta_{1}}\ ..\ \frac{\partial c}{\partial \eta_{p}}\ ]](https://delfr.com/wp-content/ql-cache/quicklatex.com-cff65739d69d763c0327b414b2f5f070_l3.png)
In Euclidean
 space, the associated column vector Gradient is denoted by
space, the associated column vector Gradient is denoted by 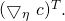
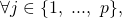 we can write:
we can write:![Rendered by QuickLaTeX.com \frac{\partial c}{\partial \eta_{j}}\ =\ \frac{\partial}{\partial \eta_{j}}\ ln\ \{{\ \int^{\infty}_{-\infty} b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ ]}\ dy\ \}} =](https://delfr.com/wp-content/ql-cache/quicklatex.com-31c9b447a69d29acfdaf2b4ae6567b36_l3.png)
![Rendered by QuickLaTeX.com \{{\ e^{-c(\eta, \Lambda)}\ \}}\ \{{\ \int^{\infty}_{-\infty}\ [\Lambda\ T(y)]_{j}\ b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ ]}\ dy\ \}} =](https://delfr.com/wp-content/ql-cache/quicklatex.com-d758d45e8fec76a6055999cd43418460_l3.png)
![Rendered by QuickLaTeX.com \int^{\infty}_{-\infty}\ [\Lambda\ T(y)]_{j}\ b(y, \Lambda)\ e^{[\ \eta^{T}\ \Lambda\ T(y)\ -\ c(\eta, \Lambda)\ ]}\ dy\ =](https://delfr.com/wp-content/ql-cache/quicklatex.com-97363060ef6abb82a441dd13e573981b_l3.png)
![Rendered by QuickLaTeX.com E[\ [\Lambda\ T(y)]_{j};\ \eta, \Lambda\ ]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e437d6413c31cef135c535790bc5dc9c_l3.png)
As a result, we conclude that:
(4)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed{(\bigtriangledown_{\eta}\ c)^{T} = \Lambda\ E[\ T(y);\ \eta, \Lambda\ ]} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-d214423a107f220a9de7d0dbd4533b61_l3.png)
The log-partition function’s Hessian: We first compute the second derivative of
 with respect to the vector
with respect to the vector 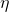 as follows:
as follows:![Rendered by QuickLaTeX.com \frac{\partial^2 c}{\partial \eta_{j}\ \partial \eta_{k}}\ =\ \frac{\partial}{\partial \eta_{k}}\ \int^{\infty}_{-\infty}\ [\Lambda\ T(y)]_{j}\ b(y, \Lambda)\ \times](https://delfr.com/wp-content/ql-cache/quicklatex.com-8ffa773bc9a243e6fd3d9399fa2dae49_l3.png)
![Rendered by QuickLaTeX.com e^{[\ \eta^{T}\ \Lambda\ T(y)\ -\ c(\eta, \Lambda)\ ]}\ dy\ =](https://delfr.com/wp-content/ql-cache/quicklatex.com-ad848e6d2b755debc0a36b5d62c3893f_l3.png)
![Rendered by QuickLaTeX.com \int^{\infty}_{-\infty}\ [\Lambda\ T(y)]_{j}\ b(y, \Lambda)\ [\ [\Lambda\ T(y)]_{k}\ -\ \frac{\partial c}{\partial \eta_{k}}\ ]\ \times](https://delfr.com/wp-content/ql-cache/quicklatex.com-83330f266ac4a8d0359717ed7e03afdf_l3.png)
![Rendered by QuickLaTeX.com e^{[\ \eta^{T}\ \Lambda\ T(y)\ -\ c(\eta, \Lambda)\ ]}\ dy\ =](https://delfr.com/wp-content/ql-cache/quicklatex.com-ad848e6d2b755debc0a36b5d62c3893f_l3.png)
![Rendered by QuickLaTeX.com E \{\ [\Lambda\ T(y)]_{j}\ [\ [\Lambda\ T(y)]_{k}\ -\ \frac{\partial c}{\partial \eta_{k}}\ ];\ \eta, \Lambda\ \}\ =](https://delfr.com/wp-content/ql-cache/quicklatex.com-d6eb11b32d3daa955afcc9e73836bee0_l3.png)
![Rendered by QuickLaTeX.com E\{\ [\Lambda\ T(y)]_{j}\ [\Lambda\ T(y)]_{k};\ \eta, \Lambda\ \}\ -](https://delfr.com/wp-content/ql-cache/quicklatex.com-11cd6ca86592907fa28c6ea37ddfff3a_l3.png)
![Rendered by QuickLaTeX.com E\{\ [\Lambda\ T(y)]_{j}\ E[\ [\Lambda\ T(y)]_{k};\ \eta, \Lambda\ ]\ \} =](https://delfr.com/wp-content/ql-cache/quicklatex.com-5dca52283254edc801c843b4a108cd71_l3.png)
![Rendered by QuickLaTeX.com E\{\ [\Lambda\ T(y)]_{j}\ [\Lambda\ T(y)]_{k};\ \eta, \Lambda\ \}\ -](https://delfr.com/wp-content/ql-cache/quicklatex.com-11cd6ca86592907fa28c6ea37ddfff3a_l3.png)
![Rendered by QuickLaTeX.com E\{\ [\Lambda\ T(y)]_{j};\ \eta, \Lambda\ \}\ \times\ E\{\ [\Lambda\ T(y)]_{k};\ \eta, \Lambda\ \}](https://delfr.com/wp-content/ql-cache/quicklatex.com-a2c51fe087333de30988f163ea9dfe7e_l3.png)
We conclude that:
(5)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed{\frac{\partial^2 c}{\partial \eta_{j}\ \partial \eta_{k}}\ =\ Cov [\ [\Lambda\ T(y)]_{j}\ ,\ [\Lambda\ T(y)]_{k};\ \eta, \Lambda\ ]} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-312c44430f941684a78d5fe182e5a42b_l3.png)
An important implication is that the Hessian of
 with respect to
with respect to 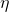 is a covariance matrix and is hence symmetric positive semi-definite. This demonstrates that
is a covariance matrix and is hence symmetric positive semi-definite. This demonstrates that  is convex in
is convex in 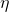 . Furthermore,
. Furthermore,  is clearly linear in
is clearly linear in 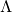 since
since ![Rendered by QuickLaTeX.com c(\eta, \Lambda)\ =\ [q(\eta)]^{T}\ \Lambda\ q(\eta).](https://delfr.com/wp-content/ql-cache/quicklatex.com-e70269d0983272b5f33a35e9b1aed27c_l3.png) As a result,
As a result,  is also convex in
is also convex in 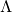 .
.
#2: A mean function ![]() that maps
that maps ![]() to the expected value of the sufficient statistic
to the expected value of the sufficient statistic ![]()
(6) ![]()
![Rendered by QuickLaTeX.com \[ E[\ T(y);\ \eta, \Lambda\ ]\ \equiv\ \begin{bmatrix} E[\ (T(y))_{1};\ \eta, \Lambda\ ]\\ ...\\ E[\ (T(y))_{p};\ \eta, \Lambda\ ]\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-28ef7e5edda7ac091baca47d98fadb14_l3.png)
We can express the mean function ![]() in terms of the log-partition function
in terms of the log-partition function ![]() or equivalently in terms of the map
or equivalently in terms of the map ![]() To do so, we first define the derivative operator of the vector-valued map
To do so, we first define the derivative operator of the vector-valued map ![]() with respect to
with respect to ![]() to be the quantity:
to be the quantity:
![Rendered by QuickLaTeX.com \[ (\mathcal{D}_{\eta}\ q)\ =\ \begin{bmatrix} \frac{\partial q_{1}}{\partial \eta_{1}} & .. & \frac{\partial q_{1}}{\partial \eta_{p}} \\ .. & .. & ..\\\frac{\partial q_{p}}{\partial \eta_{1}} & .. & \frac{\partial q_{p}}{\partial \eta_{p}} \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-a8eee3bcafbf1080651220522dbe59a6_l3.png)
Equations ![]() and
and ![]() show that:
show that:
(7) ![]()
We could also invoke the chain rule and write:
![]()
![]()
It follows that:
(8) ![]()
And hence, that:
(9) ![]()
#3: A design criteria that imposes a linear relationship between the natural parameter vector ![]() and the input
and the input ![]() Note that the linearity condition is a matter of choice and one could theoretically investigate non-linear choices including e.g., quadratic or higher order relationships. The linearity condition is expressed as
Note that the linearity condition is a matter of choice and one could theoretically investigate non-linear choices including e.g., quadratic or higher order relationships. The linearity condition is expressed as ![]() where:
where:
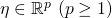
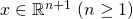 is the design vector given by
is the design vector given by ![Rendered by QuickLaTeX.com [1\ x_{1}\ ...\ x_{n}]^{T}.](https://delfr.com/wp-content/ql-cache/quicklatex.com-ff349e096e260e3cc7c588ad6e1aed2a_l3.png) The
The 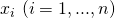 are the
are the 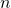 features (i.e., components of the design vector) and the leading 1 accounts for the intercept term.
features (i.e., components of the design vector) and the leading 1 accounts for the intercept term.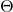 is the coefficient matrix
is the coefficient matrix 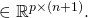 Note that
Note that 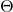 reduces to a row vector whenever
reduces to a row vector whenever 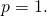
The design criteria establishes a link between input and output. In other terms, knowledge of ![]() and the mean function
and the mean function ![]() allow one to compute:
allow one to compute:
![]()
Subsequently, one can make informed predictions about the output given a certain input as we will later see in sections 6 and 7.
The special case of a dispersion parameter: In what follows, we consider the special case of a dispersion matrix ![]() equal to a positive scalar multiple
equal to a positive scalar multiple ![]() of the
of the ![]() identity matrix
identity matrix ![]() We write
We write ![]() . This case includes many of the known probability distributions including the univariate Gaussian, Bernoulli, Poisson, Geometric and Multinomial cases that we will revisit in section 6. As expected, this particular case lends itself to further simplification of the mean and the log-partition functions, as well as the latter’s Gradient and Hessian expressions:
. This case includes many of the known probability distributions including the univariate Gaussian, Bernoulli, Poisson, Geometric and Multinomial cases that we will revisit in section 6. As expected, this particular case lends itself to further simplification of the mean and the log-partition functions, as well as the latter’s Gradient and Hessian expressions:
- First, note that in this case, the form of the distribution reduces to:
(10)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed{p(y;\ \eta, \rho) = b(y, \rho)\ e^{\rho\ [\ \eta^{T}\ T(y)\ -\ [q(\eta)]^{T}\ q(\eta)\ ]}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-920d751b8f0bbf78a9c1338313c62148_l3.png)
By defining
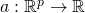 to be the map taking
to be the map taking 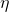 to
to ![Rendered by QuickLaTeX.com a(\eta) = [q(\eta)]^{T}\ q(\eta),](https://delfr.com/wp-content/ql-cache/quicklatex.com-ea8acfb3cf7de00dd5908ad3b19c1618_l3.png) we can rewrite the probability distribution as:
we can rewrite the probability distribution as:(11)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed{p(y;\ \eta, \rho) = b(y, \rho)\ e^{\rho\ [\ \eta^{T}\ T(y)\ -\ a(\eta)\ ]}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-93602b979a2041191c576302f8c41326_l3.png)
It becomes clear that the log-partition function can be expressed as:
(12)
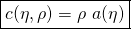
-
The Gradient of the log-partition function can also be simplified and written as:
(13)
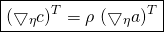
Equation
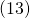 coupled with equation
coupled with equation 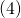 demonstrate that:
demonstrate that:(14)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed{h(\eta) = E[\ T(y);\ \eta\ ] = (\bigtriangledown_{\eta}\ a)^{T}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-e45297855cf2997674559ce5c938fd05_l3.png)
A noteworthy observation is that in this case, the mean function
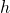 does not depend on the dispersion parameter
does not depend on the dispersion parameter 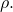 It is completely determined by the natural parameter
It is completely determined by the natural parameter 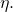
-
Lastly, note that equation
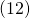 shows that:
shows that:(15)
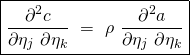
Coupled with equation
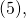 equation
equation 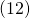 allows us to conclude that:
allows us to conclude that:(16)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed{Cov [\ [T(y)]_{j},\ [T(y)]_{k};\ \eta, \rho\ ]\ =\ \frac{1}{\rho}\ \frac{\partial^2 a}{\partial \eta_{j}\ \partial \eta_{k}}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-cb3f15f50c4c05fc50f8f96d60449cf0_l3.png)
An important implication is that the Hessian of
 with respect to
with respect to 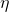 is a positive multiple of a covariance matrix and is hence positive semi-definite. This shows that
is a positive multiple of a covariance matrix and is hence positive semi-definite. This shows that  is convex in
is convex in 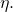
3. Generalized Linear Model Cost Function, Gradient and Hessian
The long form basic Cost Function: In order to compute ![]() and conduct predictions on a given input
and conduct predictions on a given input ![]() one first needs to decide on the dispersion matrix
one first needs to decide on the dispersion matrix ![]() and the matrix
and the matrix ![]() of coefficients. The performance of the predictive model will be dictated by the choice of
of coefficients. The performance of the predictive model will be dictated by the choice of ![]() and
and ![]() In our supervised learning setting, these two matrices will be jointly determined by:
In our supervised learning setting, these two matrices will be jointly determined by:
- The pre-defined training set
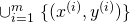 for a given integer
for a given integer 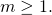
- The choice of an objective function to optimize. We refer to it as the Cost Function, denote it by
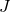 and define it as a map that takes
and define it as a map that takes 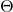 and
and 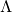 as inputs and that outputs a real number. For the purpose of this note, we derive
as inputs and that outputs a real number. For the purpose of this note, we derive 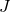 by applying the principle of Maximum Likelihood which we describe next.
by applying the principle of Maximum Likelihood which we describe next.
Define the likelihood function ![]() associated with a training set
associated with a training set ![]() to be
to be
![]()
![]()
Our objective is to find the matrices ![]() and
and ![]() that maximize
that maximize ![]() To proceed further, we assume that
To proceed further, we assume that ![]() depends only on
depends only on ![]() We get:
We get:
![]()
![]()
![]()
![]()
![]()
The presence of products coupled with the exponential nature of the conditional probability distribution makes it more appealing to invoke the natural logarithm function. Most importantly, the logarithm function is increasing on the subset of positive real numbers. This implies that maximizing the likelihood function ![]() is equivalent to maximizing the log-likelihood function
is equivalent to maximizing the log-likelihood function ![]() over all possible choices of
over all possible choices of ![]() and
and ![]() We write:
We write:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} \Sigma_{i=1}^{m}\ ln\ (\ b(y^{(i)}, \Lambda)\ )\ +\\ \\ \Sigma_{i=1}^{m}\ [\ (x^{(i)})^{T}\ \Theta^{T}\ \Lambda\ T(y^{(i)})\ -\ c(\Theta x^{(i)}, \Lambda)\ ] \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-0f066e2ba0b1e091c6c8d16aed1ca4c5_l3.png)
Finally, note that maximizing ![]() is equivalent to minimizing
is equivalent to minimizing ![]() We thus define the long form basic Cost Function to be the function:
We thus define the long form basic Cost Function to be the function:
![]() that maps
that maps ![]() to:
to:
(17) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed{\begin{gathered}J^{(LB)}(\Theta, \Lambda) = \frac{1}{m}\ \Sigma_{i=1}^{m}\ [\ c(\Theta x^{(i)}, \Lambda) -\\ (x^{(i)})^{T}\ \Theta^{T}\ \Lambda\ T(y^{(i)})\ - ln\ (\ b(y^{(i)}, \Lambda\ ))\ ]\end{gathered}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-044be290ddb251cacd6b5a1620c0cc7c_l3.png)
We use the descriptor long form to distinguish it from a shorter form associated with the special case of a dispersion matrix ![]() equal to a scalar multiple of the identity matrix. On the other hand, the basic attribute will be contrasted with a more general counterpart that will incorporate weights and a regularization parameter as we will see shortly.
equal to a scalar multiple of the identity matrix. On the other hand, the basic attribute will be contrasted with a more general counterpart that will incorporate weights and a regularization parameter as we will see shortly.
The optimal values ![]() and
and ![]() must satisfy:
must satisfy:
![]()
The long form general Cost Function: We can generalize further the Cost Function by accounting for two additional factors:
- At times, when conducting a prediction on an input
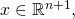 one might want to give more weight to training set points that are in the vicinity of
one might want to give more weight to training set points that are in the vicinity of 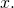 One common way of doing so is by invoking a particular weight function
One common way of doing so is by invoking a particular weight function 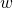 defined as follows:
defined as follows:
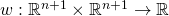
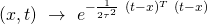
Given an input
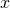 on which a prediction needs to be conducted, one can evaluate
on which a prediction needs to be conducted, one can evaluate 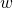 at the different training points
at the different training points 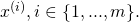 We let
We let 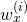 denote the quantity
denote the quantity 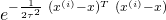 and refer to it as the weight attributed to the
and refer to it as the weight attributed to the 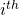 training point associated with input
training point associated with input 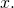
Different values of
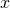 yield different weights attributed to the same training point. Moreover, larger values of the bandwidth paramter
yield different weights attributed to the same training point. Moreover, larger values of the bandwidth paramter 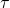 result in more inputs in the neighborhood of
result in more inputs in the neighborhood of 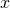 being attributed higher weights. In the extreme case when
being attributed higher weights. In the extreme case when 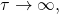 all training set inputs get a weight of
all training set inputs get a weight of 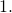
- It is common practice in convex optimization to introduce a regularization component to the objective function. The purpose of it is to penalize high values of the optimization variables. In our case, the optimization variables consist of:
- The coefficients matrix
![Rendered by QuickLaTeX.com \Theta = [\Theta_{1}\ ..\ \Theta_{p}]^{T}](https://delfr.com/wp-content/ql-cache/quicklatex.com-5852f155cf2986391dc69e0d10a7ba5f_l3.png) where
where 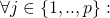
![Rendered by QuickLaTeX.com \Theta_{j}\ =\ [\theta_{j1}\ ..\ \theta_{j(n+1)}]^T](https://delfr.com/wp-content/ql-cache/quicklatex.com-0eb165a16689ecd9ddba9f21d41edac9_l3.png)
- The dispersion matrix
![Rendered by QuickLaTeX.com \Lambda = [\Lambda_{1}\ ..\ \Lambda_{p}]^{T}](https://delfr.com/wp-content/ql-cache/quicklatex.com-df988ed5c3ec557f525e4b286115c966_l3.png) where
where 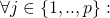
![Rendered by QuickLaTeX.com \Lambda_{j}\ =\ [\rho_{j1}\ ..\ \rho_{jp}]^T](https://delfr.com/wp-content/ql-cache/quicklatex.com-64fe7ea20574548f3d68973dc94f7af4_l3.png)
The regularization term is usually proportional to the size of the variable, where size is measured according to some norm (e.g., L2 or L1). In our case, we add a regularization term given by
![Rendered by QuickLaTeX.com \frac{\lambda}{2}\ \Sigma_{j=1}^{p}\ [\Theta_{j}^{T} \Theta_{j}\ +\Lambda_{j}^{T} \Lambda_{j}].](https://delfr.com/wp-content/ql-cache/quicklatex.com-eb516abcb1c6dcccd24e90d511cef9cf_l3.png) The
The 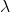 variable is the proportionality constant and the other factor is the sum of the squares of the L2 norm of each
variable is the proportionality constant and the other factor is the sum of the squares of the L2 norm of each 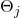 and each
and each 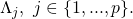
- The coefficients matrix
Given a specific ![]() and
and ![]() we denote the corresponding long form general Cost Function by
we denote the corresponding long form general Cost Function by ![]() The subscripts are meant to highlight the potential dependence on weights (as dictated by the input
The subscripts are meant to highlight the potential dependence on weights (as dictated by the input ![]() ) and on the regularization parameter
) and on the regularization parameter ![]() We have:
We have:
![]()
![]()
(18) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed { \begin{gathered} J^{(LG)}_{x, \lambda}\ (\Theta, \Lambda) = \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ \{\ c(\Theta x^{(i)}, \Lambda)\ -\\ (x^{(i)})^{T}\ \Theta^{T}\ \Lambda\ T(y^{(i)})\ -\ ln\ (b(y^{(i)}, \Lambda))\ \}\ +\\ \frac{\lambda}{2}\ \Sigma_{j=1}^{p}\ [\ \Theta_{j}^{T} \Theta_{j}\ +\Lambda_{j}^{T} \Lambda_{j}\ ] \end{gathered} } \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-54ffe27f63f2fb51cd7ee184cd5618e1_l3.png)
An important observation is that ![]() is convex in
is convex in ![]() To see why, recall from section 2 that the map
To see why, recall from section 2 that the map ![]() is convex in
is convex in ![]() Furthermore,
Furthermore, ![]() is linear in
is linear in ![]() and so
and so ![]() is convex in
is convex in ![]() . Moreover,
. Moreover, ![]() is linear in
is linear in ![]() and thus convex. Finally, one can easily show that
and thus convex. Finally, one can easily show that ![]() is also convex in
is also convex in ![]() Being a positively scaled sum of convex functions,
Being a positively scaled sum of convex functions, ![]() is thus convex in
is thus convex in ![]() This in turn implies the existence of a globally minimizing value
This in turn implies the existence of a globally minimizing value ![]()
In addition, note that all the terms appearing in ![]() are convex in
are convex in ![]() (recall that we’ve seen in section 2 that the log-partition function
(recall that we’ve seen in section 2 that the log-partition function ![]() is convex in
is convex in ![]() except possibly for the term
except possibly for the term ![]() If
If ![]() is convex in
is convex in ![]() then so will
then so will ![]() and as a result, so will
and as a result, so will ![]() This would then imply the existence of a globally minimizing
This would then imply the existence of a globally minimizing ![]()
The long form general Cost Function’s Gradient: We define the Gradient of ![]() with respect to matrices
with respect to matrices ![]() and
and ![]() to be the map:
to be the map:
![]()
![]()
(19) ![]()
where, ![]() and
and ![]() are defined as follows:
are defined as follows:
![Rendered by QuickLaTeX.com \[ \bigtriangledown_{\Theta}\ (J^{(LG)}_{x, \lambda}) = \begin{bmatrix} \bigtriangledown_{\Theta_{1}}\ (J^{(LG)}_{x, \lambda}) \\ ...\\ \bigtriangledown_{\Theta_{p}}\ (J^{(LG)}_{x, \lambda}) \end{bmatrix} = \begin{bmatrix} \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \theta_{11}} & .. & \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \theta_{1(n+1)}} \\.. & .. & .. \\ \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \theta_{p1}} & .. & \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \theta_{p(n+1)}} \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-a69e54e4cd3271665cf4fc01dd90f3ad_l3.png)
and
![Rendered by QuickLaTeX.com \[ \bigtriangledown_{\Lambda}\ (J^{(LG)}_{x, \lambda}) = \begin{bmatrix} \bigtriangledown_{\Lambda_{1}}\ (J^{(LG)}_{x, \lambda}) \\ ...\\ \bigtriangledown_{\Lambda_{p}}\ (J^{(LG)}_{x, \lambda}) \end{bmatrix} = \begin{bmatrix} \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \rho_{11}} & .. & \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \rho_{1p}} \\ .. & .. & .. \\ \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \rho_{p1}} & .. & \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \rho_{pp}} \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-ed50a2d9e624b68d41b3249266775211_l3.png)
Note that ![]() and
and ![]() are taken to be one-forms (being covariant derivatives of the scalar function
are taken to be one-forms (being covariant derivatives of the scalar function ![]() in the directions of vector
in the directions of vector ![]() and
and ![]() respectively). We subsequently represent them in Euclidean space as row vectors.
respectively). We subsequently represent them in Euclidean space as row vectors.
![]() and
and ![]() the
the ![]() component of
component of ![]() is:
is:
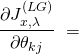
![]()
Recall that by design, we chose ![]() and so
and so ![]() As a result, the only value of
As a result, the only value of ![]() for which
for which ![]() contains the term
contains the term ![]() is
is ![]() We simplify to obtain:
We simplify to obtain:
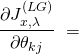
![]()
And hence conclude that:
(20) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed{\begin{gathered} \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \theta_{kj}}\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ [\ \frac{\partial c}{\partial \eta_{k}} (\Theta x^{(i)}, \Lambda)\ x_{j}^{(i)}\\ - x_{j}^{(i)}\ [\Lambda\ T(y^{(i)})]_{k}\ ]\ +\ \lambda \theta_{kj} \end{gathered}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-c1c0bbfe5406144d100d994ea4d4dbfc_l3.png)
Similarly, one finds that ![]() the
the ![]() component of
component of ![]() is:
is:
(21) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed { \begin{gathered} \frac{\partial {J}^{(LG)}_{x, \lambda}}{\partial \rho_{kj}} = \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ \{\ \frac{\partial c}{\partial \rho_{kj}} (\Theta x^{(i)}, \Lambda)\ - \\ [\Theta x^{(i)}]_{k}\ [T(y^{(i)})]_{j} - \frac{1}{b(y^{(i)}, \Lambda)} \frac{\partial b}{\partial \rho_{kj}} (y^{(i)}, \Lambda)\ \}\ +\ \lambda \rho_{kj} \end{gathered} } \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-f4eabe097fe633e174c766f2ab5c7f14_l3.png)
The long form general Cost Function’s Hessian: Let ![]() be the column vector
be the column vector ![]() whose components are given by:
whose components are given by:
![]()
We define the Hessian of the Cost Function ![]() with respect to matrices
with respect to matrices ![]() and
and ![]() to be the map:
to be the map:
![]()
![]()
![Rendered by QuickLaTeX.com \[ H_{\Theta, \Lambda}\ (J^{(LG)}_{x, \lambda}) = \begin{bmatrix} \frac{\partial^2 {J}^{(LG)}_{x, \lambda}}{\partial \alpha_{1}\ \partial \alpha_{1}} & .. & \frac{\partial^2 {J}^{(LG)}_{x, \lambda}}{\partial \alpha_{1}\ \partial \alpha_{p(p+n+1)}} \\ .. & .. & .. \\ \frac{\partial^2 {J}^{(LG)}_{x, \lambda}}{\partial \alpha_{p(p+n+1)}\ \partial \alpha_{1}} & .. & \frac{\partial^2 {J}^{(LG)}_{x, \lambda}}{\partial \alpha_{p(p+n+1)}\ \partial \alpha_{p(p+n+1)}} \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-5dffc979f1cba733321a032cb55f17cc_l3.png)
We consider three cases:
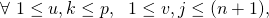 the
the 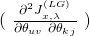 component of
component of 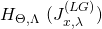 is:
is:
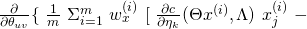
![Rendered by QuickLaTeX.com x_{j}^{(i)}\ [\Lambda\ T(y^{(i)})]_{k}\ ]\ +\ \lambda \theta_{kj}\ \}=](https://delfr.com/wp-content/ql-cache/quicklatex.com-33eb6a257f178b47432a7d27f421a903_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ x_{j}^{(i)}\ \frac{\partial }{\partial \theta_{uv}}\ [\ \frac{\partial c}{\partial \eta_{k}} (\Theta x^{(i)}, \Lambda)\ ]\ +\ \lambda \delta_{uk} \delta_{vj}](https://delfr.com/wp-content/ql-cache/quicklatex.com-1881c648c08dbbece1ced8159f17b532_l3.png)
Let
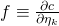 and
and 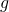 the map that takes
the map that takes 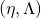 to
to 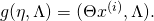 The chain rule allows us to write:
The chain rule allows us to write: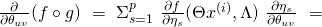
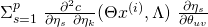
Since
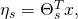 we get
we get 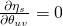 whenever
whenever 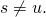 As a result:
As a result: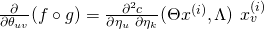
We conclude that:
(22)
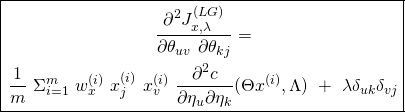
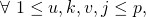 the
the 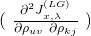 component of
component of 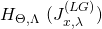 is:
is:
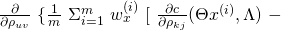
![Rendered by QuickLaTeX.com [\Theta x^{(i)}]_{k}\ [T(y^{(i)})]_{j} - \frac{1}{b(y^{(i)}, \Lambda)}\ \frac{\partial b}{\partial \rho_{kj}} (y^{(i)}, \Lambda)\ ]\ +\ \lambda \rho_{kj}\}](https://delfr.com/wp-content/ql-cache/quicklatex.com-0292e0264e16479017988101777aa7b8_l3.png)
We get:
(23)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed { \begin{gathered} \frac{\partial^2 {J}^{(LG)}_{x, \lambda}}{\partial \rho_{uv} \partial \rho_{kj}}\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ \{\ \frac{\partial^2 c}{\partial \rho_{uv} \partial \rho_{kj}} (\Theta x^{(i)}, \Lambda)\ +\\ \frac{1}{[b(y^{(i)}, \Lambda)]^{2}}\ [\ \frac{\partial b}{\partial \rho_{uv}} (y^{(i)}, \Lambda)\ \ \frac{\partial b}{\partial \rho_{kj}} (y^{(i)}, \Lambda)\ -\\ b(y^{(i)}, \Lambda)\ \frac{\partial^2 b}{\partial \rho_{uv}\ \partial \rho_{kj}} (y^{(i)}, \Lambda)\ ]\ \}\ +\ \lambda \delta_{uk} \delta_{vj} \end{gathered} } \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-88cc9e6392b227b10b8e3f1a9b626872_l3.png)
 the
the 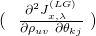 and
and 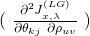 components of
components of 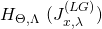 are equal and are given by:
are equal and are given by:
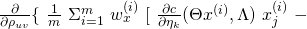
![Rendered by QuickLaTeX.com x_{j}^{(i)} [\Lambda\ T(y^{(i)})]_{k}\ ]\ +\ \lambda \theta_{kj}\ \}](https://delfr.com/wp-content/ql-cache/quicklatex.com-688f084fdf844a41cc26c1f393ddec12_l3.png)
We get:
(24)
![Rendered by QuickLaTeX.com \begin{equation*} \boxed { \begin{gathered} \frac{\partial^2 J^{(LG)}_{x, \lambda}}{\partial \rho_{uv}\ \partial \theta_{kj}}\ =\ \frac{\partial^2 J^{(LG)}_{x, \lambda}}{\partial \theta_{kj}\ \partial \rho_{uv}}\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ [\\ \frac{\partial^2 c}{\partial \rho_{uv}\ \partial \eta_{k}} (\Theta x^{(i)}, \Lambda)\ x_{j}^{(i)}\ -\ x_{j}^{(i)} [T(y^{(i)})]_{v}\ \delta_{uk}\ ] \end{gathered} } \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-d76ddf786ca8cd0297fabc07a1908267_l3.png)
The short form basic Cost Function: With the exception of the multivariate Gaussian distribution, all the other probability distributions that we consider in this note have a dispersion matrix that is a positive scalar multiple of the identity matrix. For this particular case, equations ![]() and
and ![]() in section 2 showed that:
in section 2 showed that:
- The log partition function is given by
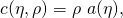 where
where 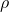 is now a positive scalar and
is now a positive scalar and 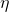 is the natural parameter vector.
is the natural parameter vector. - The mean function
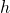 is independent of the dispersion parameter
is independent of the dispersion parameter 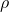 and depends solely on the natural parameter
and depends solely on the natural parameter 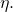 We write
We write 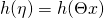 for a given coefficient matrix
for a given coefficient matrix  and input vector
and input vector 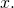
In what follows, we simplify the expression of the Cost Function associated with such a case and derive simpler formulae for the components of its Gradient and its Hessian. By substituting the matrix ![]() with
with ![]() (where
(where ![]() and
and ![]() in equation
in equation ![]() and by applying equation
and by applying equation ![]() we can write:
we can write:
![]()
![]()
Minimizing ![]() with respect to
with respect to ![]() is equivalent to minimizing the following quantity with respect to
is equivalent to minimizing the following quantity with respect to ![]() :
:
![]()
And since ![]() is a positive scalar, the optimal value of
is a positive scalar, the optimal value of ![]() that minimizes this quantity is the same as the one that minimizes the following quantity:
that minimizes this quantity is the same as the one that minimizes the following quantity:
(25) ![]()
We refer to ![]() as the short form basic Cost Function. An important observation is that
as the short form basic Cost Function. An important observation is that ![]() depends exclusively on
depends exclusively on ![]() And since in this particular case the mean function
And since in this particular case the mean function ![]() also depends only on
also depends only on ![]() one can find the optimal coefficient matrix by minimizing
one can find the optimal coefficient matrix by minimizing ![]() and then plugging it into
and then plugging it into ![]() to conduct predictions.
to conduct predictions.
Equally important is the fact that ![]() is convex in
is convex in ![]() The proof is similar to the one we previously used to establish the convexity of
The proof is similar to the one we previously used to establish the convexity of ![]() in
in ![]()
The short form general Cost Function: The same approach used to derive the long form general Cost Function from its basic counterpart can be applied to obtain the following short form general Cost Function:
Given a specific ![]() and
and ![]() the corresponding short form general Cost Function is the map
the corresponding short form general Cost Function is the map ![]() that takes
that takes ![]() to:
to:
(26) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed{\begin{gathered} {J}^{(SG)}_{x, \lambda}(\Theta)\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}[\ a(\Theta x^{(i)})\\ -\ (x^{(i)})^{T}\ \Theta^{T}\ T(y^{(i)})\ ]\ +\ \frac{\lambda}{2}\ \Sigma_{j=1}^{p}\ \Theta_{j}^{T} \Theta_{j} \end{gathered}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-08035f5646c7524defb50e027ad96eb6_l3.png)
The short form general Cost Function’s Gradient: We define the Gradient of ![]() with respect to the matrix
with respect to the matrix ![]() to be the map:
to be the map:
![]()
![Rendered by QuickLaTeX.com \[ \Theta\ \rightarrow\ \bigtriangledown_{\Theta}\ (J^{(SG)}_{x, \lambda}) = \begin{bmatrix} \bigtriangledown_{\Theta_{1}}\ (J^{(SG)}_{x, \lambda}) \\ ...\\ \bigtriangledown_{\Theta_{p}}\ (J^{(SG)}_{x, \lambda}) \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial {J}^{(SG)}_{x, \lambda}}{\partial \theta_{11}} & .. & \frac{\partial {J}^{(SG)}_{x, \lambda}}{\partial \theta_{1(n+1)}} \\ .. & .. & .. \\ \frac{\partial {J}^{(SG)}_{x, \lambda}}{\partial \theta_{p1}} & .. & \frac{\partial {J}^{(SG)}_{x, \lambda}}{\partial \theta_{p(n+1)}} \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-b41f3553e2a4460f18a29eb9232fbef0_l3.png)
![]() and
and ![]() the
the ![]() component of
component of ![]() is:
is:
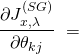
![]()
Recall that by design, we chose ![]() and so
and so ![]() As a result, the only value of
As a result, the only value of ![]() for which
for which ![]() contains the term
contains the term ![]() is
is ![]() This allows us to write
This allows us to write
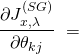
![]()
And hence conclude that:
(27) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed{\begin{gathered} \frac{\partial J^{(SG)}_{x, \lambda}}{\partial \theta_{kj}}\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ [\ \frac{\partial a}{\partial \eta_{k}} (\Theta x^{(i)})\ x_{j}^{(i)}\ -\\ x_{j}^{(i)}\ [T(y^{(i)})]_{k}\ ]\ +\ \lambda \theta_{kj} \end{gathered}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-f1082898f3fc2dc4bcf38abcdedbf90d_l3.png)
The short form general Cost Function’s Hessian: We define the Hessian of ![]() with respect to the matrix
with respect to the matrix ![]() to be the map:
to be the map:
![]()
![Rendered by QuickLaTeX.com \[ \Theta\ \rightarrow\ H_{\Theta}\ (J^{(SG)}_{x, \lambda}) = \begin{bmatrix} (H_{11})_{\Theta} & .. & (H_{1p})_{\Theta} \\ .. & .. & .. \\ (H_{p1})_{\Theta} & .. & (H_{pp})_{\Theta} \\ \end{bmatrix} (J_{x, \lambda}^{(SG)}) \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-8462e1efc48315aab71390525d1ee807_l3.png)
where ![]() the block matrix
the block matrix ![]() is:
is:
![Rendered by QuickLaTeX.com \[ (H_{uk})_{\Theta}\ (J_{x, \lambda}^{(SG)}) = \begin{bmatrix} \frac{\partial^2 J^{(SG)}_{x, \lambda}}{\partial \theta_{u1}\ \partial \theta_{k1}} & .. & \frac{\partial^2 J^{(SG)}_{x, \lambda}}{\partial \theta_{u1}\ \partial \theta_{k(n+1)}} \\ .. & .. & .. \\ \frac{\partial^2 J^{(SG)}_{x, \lambda}}{\partial \theta_{u(n+1)}\ \partial \theta_{k1}} & .. & \frac{\partial^2 J^{(SG)}_{x, \lambda}}{\partial \theta_{u(n+1)}\ \partial \theta_{k(n+1)}} \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-3c21a8b4fc1c0be4a335faf7e0aaaa1f_l3.png)
![]() and
and ![]() the components of
the components of ![]() are:
are:
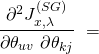
![]()
![]()
Let ![]() and
and ![]() be the function mapping
be the function mapping ![]() to
to ![]() The chain rule allows us to write:
The chain rule allows us to write:
![]()
![]()
Since ![]() we conclude that:
we conclude that:
(28) 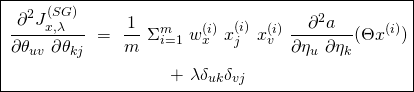
4. Matricial formulation of the Cost Function, its Gradient, and its Hessian
In this section, we limit ourselves to the short form general Cost Function ![]() Since there is no room for confusion, we will drop the superscript
Since there is no room for confusion, we will drop the superscript ![]() refer to it simply as the Cost Function and denote it by
refer to it simply as the Cost Function and denote it by ![]() In order to derive a concise notation for
In order to derive a concise notation for ![]() its Gradient
its Gradient ![]() , and its Hessian
, and its Hessian ![]() we first introduce relevant vectorial and matricial quantities. In what follows, we recall that
we first introduce relevant vectorial and matricial quantities. In what follows, we recall that ![]() denotes the dimension of the sufficient statistic
denotes the dimension of the sufficient statistic ![]()
![]() denotes that of
denotes that of ![]() ,
, ![]() denotes the number of input features and
denotes the number of input features and ![]() denotes the number of training examples.
denotes the number of training examples.
- The coefficient matrix
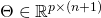 is given by:
is given by: ![Rendered by QuickLaTeX.com \[ \Theta =\begin{bmatrix}\Theta_{1}^T\\...\\\Theta_{p}^T\\\end{bmatrix}=\begin{bmatrix}\theta_{11} & .. & \theta_{1(n+1)} \\.. & .. & .. \\\theta_{p1} & .. & \theta_{p(n+1)}\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e27a7ccf7b906dba59dbd8c3de3f833e_l3.png)
- The design matrix
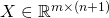 is given by:
is given by: ![Rendered by QuickLaTeX.com \[X =\begin{bmatrix}x^{(1)T}\\...\\x^{(m)T}\\\end{bmatrix}=\begin{bmatrix}1 & x_{1}^{(1)} & .. & x_{n}^{(1)} \\1 & .. & .. & .. \\1 & x_{1}^{(m)} & .. & x_{n}^{(m)} \\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-a4c8125752993b8419ede5d80bba0284_l3.png)
- The target matrix
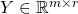 for some
for some 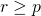 is given by:
is given by: ![Rendered by QuickLaTeX.com \[Y =\begin{bmatrix}y^{(1)T}\\...\\y^{(m)T}\\\end{bmatrix}=\begin{bmatrix}y_{1}^{(1)} & .. & y_{r}^{(1)} \\.. & .. & .. \\y_{1}^{(m)} & .. & y_{r}^{(m)} \\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e0303a12b0b790202875e0b578866243_l3.png)
- The sufficient statistic matrix
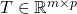 is given by:
is given by: ![Rendered by QuickLaTeX.com \[T =\begin{bmatrix}T(y^{(1)})^{T}\\...\\T(y^{(m)})^{T}\\\end{bmatrix}=\begin{bmatrix}t_{1}^{(1)} & .. & t_{p}^{(1)} \\.. & .. & .. \\t_{1}^{(m)} & .. & t_{p}^{(m)} \\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-c5b3e32f57a696af15436d9dfa642c6b_l3.png)
- The weight matrix
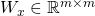 associated with input
associated with input 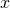 and weight function
and weight function 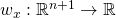 is given by:
is given by: ![Rendered by QuickLaTeX.com \[W_{x} =\begin{bmatrix}w_{x}^{(1)} & 0 & 0 & .. & 0 \\0 & w_{x}^{(2)} & 0 & .. & 0 \\.. & .. & .. & .. & .. \\0 & 0 & 0 & .. & w_{x}^{(m)} \\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-a51cb6f760921b35ba0a8698273e0a1d_l3.png)
- The regularization matrix
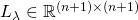 associated with parameter
associated with parameter 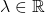 is given by:
is given by: ![Rendered by QuickLaTeX.com \[L_{\lambda} =\begin{bmatrix}\lambda & 0 & 0 & .. & 0 \\0 & \lambda & 0 & .. & 0 \\.. & .. & .. & .. & .. \\0 & 0 & 0 & .. & \lambda \\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-7f8621008f324305d1584f37eb16c47a_l3.png)
- The log-partition vector
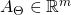 associated with the log-partition function
associated with the log-partition function 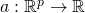 that maps
that maps ![Rendered by QuickLaTeX.com \eta \equiv [\eta_{1}\ ...\ \eta_{p}]^{T}](https://delfr.com/wp-content/ql-cache/quicklatex.com-a7e29cbd724bf4a4c9acedadcd03cfee_l3.png) to
to ![Rendered by QuickLaTeX.com a(\eta) = [q(\eta)]^{T}\ q(\eta)](https://delfr.com/wp-content/ql-cache/quicklatex.com-b75be292b069f39654a60326a0041c04_l3.png) is given by:
is given by: ![Rendered by QuickLaTeX.com \[A_{\Theta} =\begin{bmatrix}a(\Theta x^{(1)})\\...\\a(\Theta x^{(m)})\\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-2b9905886b95745bf32fe089979287fb_l3.png)
- The log-partition Gradient matrix
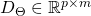 is given by:
is given by: ![Rendered by QuickLaTeX.com \[D_{\Theta} =\begin{bmatrix}\frac{\partial a}{\partial \eta_{1}} (\Theta x^{(1)}) & .. & \frac{\partial a}{\partial \eta_{1}} (\Theta x^{(m)}) \\.. & .. & .. \\\frac{\partial a}{\partial \eta_{p}} (\Theta x^{(1)}) & .. & \frac{\partial a}{\partial \eta_{p}} (\Theta x^{(m)}) \\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-c5a53ac1391b96cdc4fc3f9053e1dcb8_l3.png)
- The second order diagonal matrix
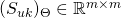 where
where 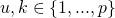 is given by:
is given by: ![Rendered by QuickLaTeX.com \[(S_{uk})_{\Theta} =\begin{bmatrix}\frac{\partial^2 a}{\partial \eta_{u}\ \partial \eta_{k}} (\Theta x^{(1)}) & .. & 0 \\.. & .. & .. \\0 & .. & \frac{\partial^2 a}{\partial \eta_{u}\ \partial \eta_{k}} (\Theta x^{(m)}) \\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-c0b7b9e10633b592c51be72ac667a58a_l3.png)
- The unit vector
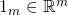 is given by:
is given by: ![Rendered by QuickLaTeX.com \[\mathbbm{1}_{m} =\begin{bmatrix}1\\...\\1\\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e293e34da44deef2b35ddf758779fdc2_l3.png)
The Cost Function in matrix form: Let ![]() and
and ![]() denote the
denote the ![]() row of
row of ![]() and
and ![]() the
the ![]() column of
column of ![]() If we have that
If we have that ![]() then, one can easily see that
then, one can easily see that ![]()
Substituting ![]() and
and ![]() with matrices
with matrices ![]() and
and ![]() respectively, one concludes that the diagonal elements of
respectively, one concludes that the diagonal elements of ![]() are
are ![]() where
where ![]() Furthermore, multiplying this matricial product by the diagonal weight matrix
Furthermore, multiplying this matricial product by the diagonal weight matrix ![]() one can see that the diagonal elements of the product
one can see that the diagonal elements of the product ![]() are given by
are given by ![]()
As a result, we can rewrite equation ![]() more concisely in matrix form as:
more concisely in matrix form as:
(29) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed{\begin{gathered} J_{x, \lambda}(\Theta)\ =\ \frac{1}{m}\ [\ \mathbbm{1}_{m}^{T}\ W_{x}\ A_{\Theta}\ -\ Tr(X\ \Theta^{T}\ T^{T}\ W_{x})\ ]\\ +\ \frac{\lambda}{2}\ Tr(\ \Theta\ \Theta^{T}\ ) \end{gathered}} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-2134098e97564862b13cb66f04b7b1d6_l3.png)
The Gradient of the Cost Function in matrix form: Using the same observation made in the previous paragraph regarding the product of three matrices, one can rewrite equation ![]() in a more concise matrix notation as follows:
in a more concise matrix notation as follows:
(30) ![]()
The Hessian of the Cost Function in matrix form: Similary, we can rewrite equation ![]() in matrix notation as follows:
in matrix notation as follows:
(31) 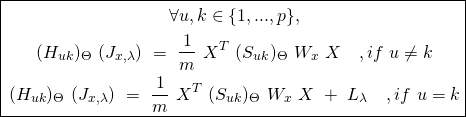
5. Algorithms to minimize the convex Cost Function
In this section too, we limit ourselves to the short form general Cost Function ![]() Our objective is to find the optimal
Our objective is to find the optimal ![]() If the weight functions
If the weight functions ![]() are independent of
are independent of ![]() for all training examples
for all training examples ![]() then
then ![]() will not depend on
will not depend on ![]() and once it is computed for a given input, it can be stored and used for all other inputs. This is known as a parametric setting. If the weight functions depend on
and once it is computed for a given input, it can be stored and used for all other inputs. This is known as a parametric setting. If the weight functions depend on ![]() then each
then each ![]() will have a different
will have a different ![]() associated with it. This procedure is known as non-parametric and is clearly computationally more demanding than its parametric counterpart. In what follows, we introduce three numerical methods for finding
associated with it. This procedure is known as non-parametric and is clearly computationally more demanding than its parametric counterpart. In what follows, we introduce three numerical methods for finding ![]()
- Batch Gradient Descent (BGD): Suppose
 is a differentiable convex function of one variable. Starting at any
is a differentiable convex function of one variable. Starting at any  one can get
one can get 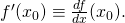 If its negative (positive), then at
If its negative (positive), then at 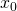 the function is decreasing (increasing). As a result, to get closer to the value of
the function is decreasing (increasing). As a result, to get closer to the value of 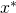 that minimizes
that minimizes 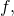 one can try a value
one can try a value 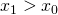 (
( ).
). One way of updating the value of
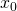 is by letting
is by letting 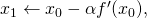 for some positive learning rate
for some positive learning rate 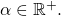 This procedure can be repeated until convergence. Note however, that the choice of
This procedure can be repeated until convergence. Note however, that the choice of 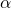 is critical since too large a value will cause divergence, while a value that is too small will cause slow convergence.
is critical since too large a value will cause divergence, while a value that is too small will cause slow convergence.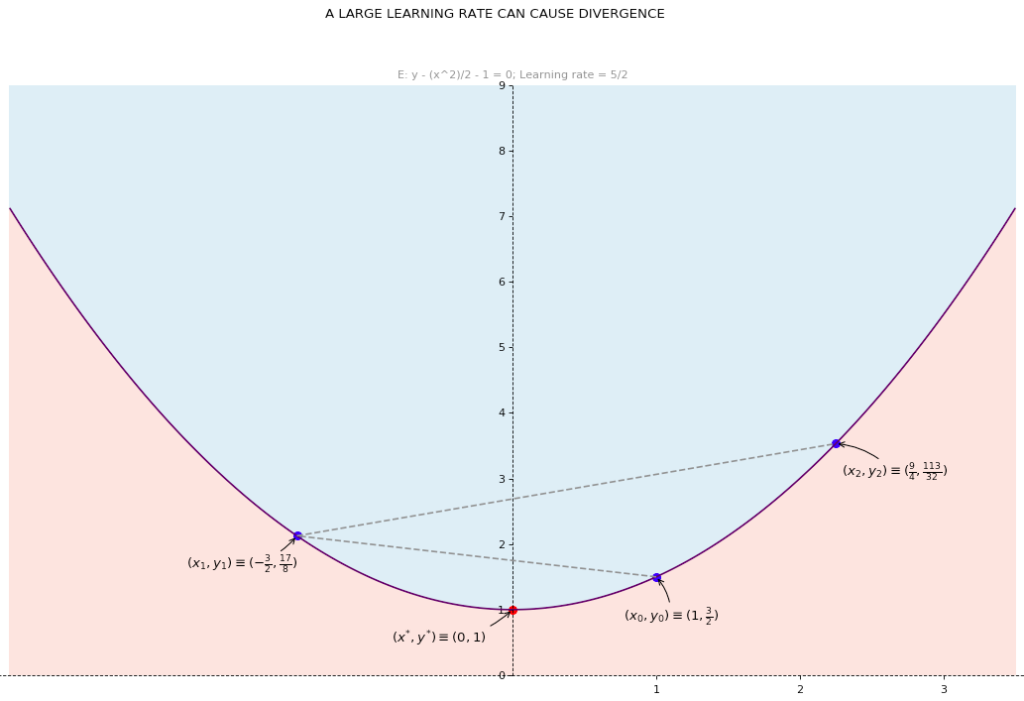
The same can be said of differentiable functions of
 variables (
variables (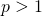 ) where this logic gets applied to each variable. In this context, we replace
) where this logic gets applied to each variable. In this context, we replace 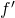 with the Gradient of
with the Gradient of 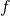 and the learning rate
and the learning rate 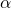 with the learning rate matrix
with the learning rate matrix 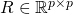 defined as:
defined as:![Rendered by QuickLaTeX.com \[ R = \begin{bmatrix} \alpha & 0 & 0 & .. & 0 \\ 0 & \alpha & 0 & .. & 0 \\ .. & .. & .. & .. & .. \\ 0 & 0 & 0 & .. & \alpha \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-2d168c4eaf72d3065c15aa3bb6dbb109_l3.png)
One can estimate the optimal matrix
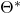 by running the following algorithm known as Batch Gradient Descent (BGD). We let iter denote an iteration count variable and max-iter denote the maximum number of allowed iterations before testing for convergence:
by running the following algorithm known as Batch Gradient Descent (BGD). We let iter denote an iteration count variable and max-iter denote the maximum number of allowed iterations before testing for convergence: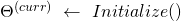
(It could be initialized to e.g., the zero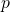 by
by 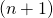 matrix).
matrix).For (iter
 max-iter)
max-iter)
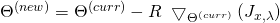
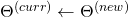
Update all the
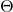 -dependent quantities including
-dependent quantities including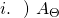
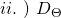
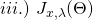
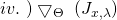
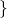
So
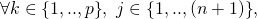 the following update is performed:
the following update is performed:
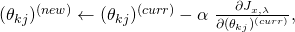
where we have:
![Rendered by QuickLaTeX.com \frac{\partial J_{x, \lambda}}{\partial \theta_{kj}}\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ [\ \frac{\partial a}{\partial \eta_{k}} (\Theta x^{(i)})\ x_{j}^{(i)}\ -\ x_{j}^{(i)}\ t_{k}^{(i)}\ ]\ +\ \lambda \theta_{kj}](https://delfr.com/wp-content/ql-cache/quicklatex.com-8b817c0e70cb67adcc46b4c8e2537c3f_l3.png)
and where
![Rendered by QuickLaTeX.com t^{(i)}_{k} \equiv [T(y^{(i)})]_{k}](https://delfr.com/wp-content/ql-cache/quicklatex.com-cac3cdeb26971e857d2af0e0698a8f8a_l3.png)
Note that BGD requires that all the entries of the new coefficient matrix
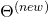 be simultaneously updated before they can be used in the next iteration.
be simultaneously updated before they can be used in the next iteration. - Stochastic Gradient Descent (SGD):In BGD, everytime we updated the value of
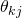 we had to perform a summation over all training examples as mandated by
we had to perform a summation over all training examples as mandated by 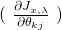 . In SGD, we drop the summation to achieve faster updates of the coefficients. In other terms, for each training example
. In SGD, we drop the summation to achieve faster updates of the coefficients. In other terms, for each training example 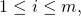 and
and 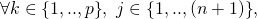 SGD conducts the following update round:
SGD conducts the following update round: ![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} (\theta_{kj})^{(new)} \leftarrow (\theta_{kj})^{(curr)}\ -\ \frac{\alpha}{m}\ w^{(i)}_{x}\ [\ \frac{\partial a}{\partial \eta_{k}} (\Theta^{(curr)}\ x^{(i)})\ x_{j}^{(i)}$$-\\ x_{j}^{(i)}\ t_{k}^{(i)}\ ]\ +\ \lambda (\theta_{kj})^{(curr)} \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-7f90a472ad422a6cc5546d3057761893_l3.png)
The entries of the new coefficient matrix
 must get simultaneously updated for each training example in each iteration before they can be used in the next instance. SGD usually achieves acceptable convergence faster than BGD, especially when the size
must get simultaneously updated for each training example in each iteration before they can be used in the next instance. SGD usually achieves acceptable convergence faster than BGD, especially when the size  of the training set is very large
of the training set is very largeIn order to describe the SGD algorithm in a more concise matrix form, we define a set of
 new matrices
new matrices 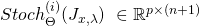 where
where 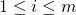 and where the
and where the 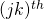 entry is given by:
entry is given by:![Rendered by QuickLaTeX.com [Stoch_{\Theta}^{(i)} (J_{x, \lambda})]_{jk}\ =\ \frac{w_{x}^{(i)}}{m}\ [\frac{\partial a}{\partial \eta_{j}} (\Theta x^{(i)}) x_{k}^{(i)} - x_{k}^{(i)} t_{j}^{(i)}] + \lambda \theta_{jk}](https://delfr.com/wp-content/ql-cache/quicklatex.com-f6446f206eaddb0901447a3c1b3ad46c_l3.png)
SGD is a variant of BGD that runs the following algorithm:
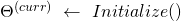
(It could be initialized to e.g., the zero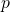 by
by  matrix).
matrix).For (iter
 max-iter)
max-iter)
For (
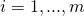 )
)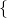
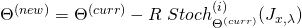
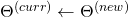
Update all the
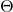 -dependent quantities including
-dependent quantities including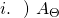
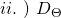
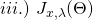
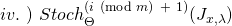
- Newton-Raphson (NR): The choice of the learning rate
 used in BGD and SGD is of special importance since it can either cause divergence or help achieve faster convergence. One limiting factor in the implementation of the previous Gradient descent algorithms is the fixed nature of
used in BGD and SGD is of special importance since it can either cause divergence or help achieve faster convergence. One limiting factor in the implementation of the previous Gradient descent algorithms is the fixed nature of 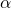 . Computational complexity aside, it would be beneficial if at every iteration, the algorithm could dynamically choose an appropriate
. Computational complexity aside, it would be beneficial if at every iteration, the algorithm could dynamically choose an appropriate 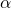 so as to reduce the number of steps needed to achieve convergence. Enters the Newton Raphson (NR) method.To motivate it, we lean on a Taylor series expansion of the Cost Function
so as to reduce the number of steps needed to achieve convergence. Enters the Newton Raphson (NR) method.To motivate it, we lean on a Taylor series expansion of the Cost Function 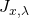 about a point (i.e., coefficient matrix)
about a point (i.e., coefficient matrix) 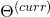 up to first order. We get:
up to first order. We get: 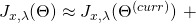
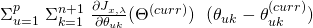
If we want to get to the optimal
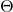 in one step, we need to set
in one step, we need to set 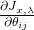 to
to 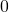 when evaluated at
when evaluated at 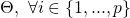 and
and 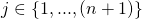 . Taking the first derivative with respect to
. Taking the first derivative with respect to 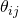 of the right and left hand sides of the approximation, and noting that
of the right and left hand sides of the approximation, and noting that 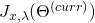 is a constant and
is a constant and 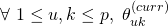 are constants, we get:
are constants, we get: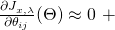
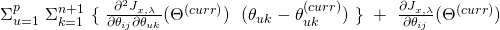
Setting
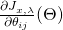 to 0 for all i
to 0 for all i 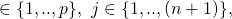 we get:
we get: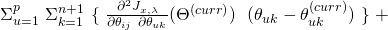
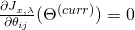
Recall that
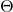 and
and 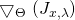 are both elements of
are both elements of 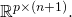 We define the vectorized versions of
We define the vectorized versions of 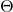 and
and 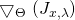 to be the elements of
to be the elements of 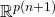 given by:
given by:![Rendered by QuickLaTeX.com \[ vect(\Theta) \equiv \begin{bmatrix} \Theta_{1}\\ ..\\ ..\\ \Theta_{p}\\ \end{bmatrix} = \begin{bmatrix} \theta_{11}\\ ..\\ \theta_{1(n+1)}\\ ..\\ ..\\ \theta_{p1}\\ ..\\ \theta_{p(n+1)}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-51fc7b234e146d2ed17d96901fbc0015_l3.png)
![Rendered by QuickLaTeX.com \[ vect(\bigtriangledown_{\Theta}\ (J_{x, \lambda})) \equiv \begin{bmatrix} [\bigtriangledown_{\Theta_{1}}\ (J_{x, \lambda})]^{T}\\ ..\\ ..\\ [\bigtriangledown_{\Theta_{p}}\ (J_{x, \lambda})]^{T}\\ \end{bmatrix} = \begin{bmatrix} \frac{\partial J_{x, \lambda}}{\partial \theta_{11}}\\ ..\\ \frac{\partial J_{x, \lambda}}{\partial \theta_{1(n+1)}}\\ ..\\ ..\\ \frac{\partial J_{x, \lambda}}{\partial \theta_{p1}}\\ ..\\ \frac{\partial J_{x, \lambda}}{\partial \theta_{p(n+1)}}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-03666505696df0451375302ab93473ad_l3.png)
We can subsequently write the above conditions in a more concise matrix form as follows:
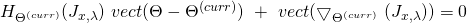
Which gives the following NR algorithm:
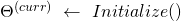
(It could be initialized to e.g., the zero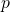 by
by  matrix).
matrix).For (iter
 max-iter)
max-iter)
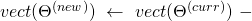
![Rendered by QuickLaTeX.com [H_{\Theta^{(curr)}}\ (J_{x, \lambda})]^{-1}\ vect(\bigtriangledown_{\Theta^{(curr)}}\ (J_{x, \lambda}))](https://delfr.com/wp-content/ql-cache/quicklatex.com-afdfad1183ea03843d8a1d3d170f117d_l3.png)
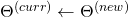
Update all the
 -dependent quantities including
-dependent quantities including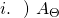
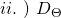
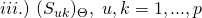
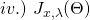
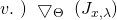
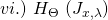
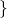
Here too, the update rule is simultaneous. This means that we keep using
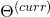 until all entries have been calculated, at which point we update
until all entries have been calculated, at which point we update 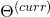 to
to 
NR is usually faster to converge when measured in terms of number of iterations. However, convergence depends on the invertibility of the Hessian at each iteration. This is not always guaranteed (e.g., multinomial classification with more than two classes). Alternatively, one could circumvent this problem by applying a modified version of NR as described in e.g., [2]. Furthermore, even when convergence is guaranteed, NR can be computationally taxing due to the matrix inversion operation at each iteration. Taking that into account, usage of NR is usually preferred whenever the dimensions of
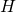 are small (i.e., small
are small (i.e., small 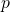 and
and 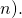
6. Specific distribution examples
In what follows, we consider a number of probability distributions whose dispersion matrix is of the form ![]() where
where ![]() is a positive dispersion scalar and
is a positive dispersion scalar and ![]() is the
is the ![]() identity matrix for
identity matrix for ![]() In order to devise the relevant discriminative supervised learning model associated with an instance of the class of such distributions, we proceed as follows:
In order to devise the relevant discriminative supervised learning model associated with an instance of the class of such distributions, we proceed as follows:
Step 1: Identify the dimensions of the target matrix ![]() where
where ![]() is the number of training examples and
is the number of training examples and ![]() the dimension of each output.
the dimension of each output.
Step 2: Identify the natural parameter ![]() and dispersion parameter
and dispersion parameter ![]() associated with the exponential distribution, compute the sufficient statistic matrix
associated with the exponential distribution, compute the sufficient statistic matrix ![]() compute the non-negative base measure
compute the non-negative base measure ![]() and derive the log-partition function
and derive the log-partition function ![]() Identify the dimensions of the coefficient matrix
Identify the dimensions of the coefficient matrix ![]()
Step 3: Compute the set of ![]() functions
functions ![]()
Step 4: If needed (e.g., in the case of NR algorithm), compute the set of ![]() functions
functions ![]()
Step 5: Compute the log-partition vector ![]()
Step 6: Compute the log-partition Gradient matrix ![]()
Step 7: If needed (e.g., in the case of NR algorithm), compute the set of ![]() second order diagonal matrices
second order diagonal matrices ![]()
Step 8: Compute the Cost Function ![]() , its Gradient
, its Gradient ![]() and its Hessian
and its Hessian ![]()
Step 9: Calculate the optimal ![]() using e.g., BGD, SGD, NR or using a closed form solution if applicable.
using e.g., BGD, SGD, NR or using a closed form solution if applicable.
Step 10: Test the model on an adequate test set and then conduct predictions on new input using the mean function ![]() that maps
that maps ![]() to
to
![Rendered by QuickLaTeX.com \[ h(\eta) = \begin{bmatrix} \frac{\partial a}{\partial \eta_{1}} (\Theta\ x)\\ ..\\ \frac{\partial a}{\partial \eta_{p}} (\Theta\ x)\\ \end{bmatrix} = E[T(y)\ |\ x; \Theta] \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-00f38e4d6262d7bc3591ab79e986f64e_l3.png)
i. The univariate Gaussian distribution: The corresponding probability distribution is:
![]()
We rewrite it in an equivalent form that makes it easier to identify as a member of the exponential family:
![]()
Step 1: The target matrix ![]() In other terms, each training example
In other terms, each training example ![]() has a univariate output
has a univariate output ![]() associated with it.
associated with it.
Step 2: We identify the following quantities:
- The natural parameter
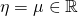
- The sufficient statistic
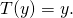 Matrix
Matrix 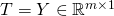 (here,
(here, 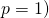
- The dispersion matrix is
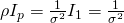
- The non-negative base measure is
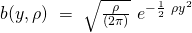
- The log-partition function maps
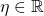 to:
to:
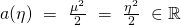
- The coefficient matrix is a row vector
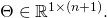
Step 3: The function ![]() is the identity map that takes
is the identity map that takes ![]() to
to ![]()
Step 4: If needed (e.g., in the case of NR algorithm), the function ![]() maps
maps ![]() to the constant value
to the constant value ![]()
Step 5: The log-partition vector is given by:
![Rendered by QuickLaTeX.com \[ A_{\Theta}\ =\ \frac{1}{2} \begin{bmatrix} (\Theta\ x^{(1)})^{2}\\ ..\\ ..\\ (\Theta\ x^{(m)})^{2}\\ \end{bmatrix} \in \mathbb{R}^{m} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-3b60eee9a4cb2db9eef25b691904ee7b_l3.png)
Step 6: The log-partition Gradient matrix is:
![]()
Step 7: If needed (e.g., in the case of NR algorithm), the second order diagonal matrix ![]() is the
is the ![]() by
by ![]() identity matrix
identity matrix ![]()
Step 8: Compute the Cost Function ![]() , its Gradient
, its Gradient ![]() and its Hessian
and its Hessian ![]()
Step 9: Calculate the optimal ![]() using e.g., BGD, SGD, NR.
using e.g., BGD, SGD, NR.
Step 10: Test the model on an adequate test set and then conduct predictions on new input using the mean function ![]() that maps
that maps ![]() to:
to:
![]()
The supervised learning model associated with the univariate Gaussian distribution coincides with the familiar linear regression model when we consider the short form basic Cost Function ![]() . Recall that the basic form has no dependence on either the regularization parameter
. Recall that the basic form has no dependence on either the regularization parameter ![]() or the input
or the input ![]() In this case, the weight matrix
In this case, the weight matrix ![]() is equal to
is equal to ![]() and the regularization matrix
and the regularization matrix ![]() is equal to
is equal to ![]()
To see this equivalence, we rewrite equation ![]() as:
as:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} J^{(SB)}(\Theta)\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ [\ a(\Theta\ x^{(i)})\ -\ [T(y^{(i)})]^{T}\ \Theta\ x^{(i)}\ ]\ = \\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ [\ \frac{1}{2}\ (\Theta\ x^{(i)})^{2}\ -\ y^{(i)}\ \Theta x^{(i)}\ ]\ = \\ \frac{1}{2m}\ \Sigma_{i=1}^{m}\ (y^{(i)} - \Theta x^{(i)})^{2}\ -\ \frac{1}{2m}\ \Sigma_{i=1}^{m}\ (y^{(i)})^{2} \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-de19652ea415bc2be6336616f0253fba_l3.png)
Minimizing ![]() over
over ![]() is equivalent to minimizing
is equivalent to minimizing ![]() over
over ![]() We thus retrieve the familiar least-square model.
We thus retrieve the familiar least-square model.
It also turns out that one can calculate the optimal coefficient matrix ![]() in closed form. Recalling that
in closed form. Recalling that ![]() is convex in
is convex in ![]() we can find
we can find ![]() by setting
by setting ![]() equal 0. Substituting
equal 0. Substituting ![]() with
with ![]() with
with ![]() with
with ![]() and
and ![]() with
with ![]() in equation
in equation ![]() we get:
we get:
![]()
Setting this Gradient to ![]() leads to the normal equation that allows us to solve for
leads to the normal equation that allows us to solve for ![]() in closed form:
in closed form:
![]()
ii. The Bernoulli (Binomial) distribution: The corresponding probability distribution is:
![]()
where the outcome ![]() is an element of
is an element of ![]() and where
and where ![]() and
and ![]() We rewrite it in an equivalent form that makes it easier to identify as a member of the exponential family:
We rewrite it in an equivalent form that makes it easier to identify as a member of the exponential family:
![]()
Step 1: The target matrix ![]() In other terms, each training example
In other terms, each training example ![]() has a binary output
has a binary output ![]() associated with it.
associated with it.
Step 2: We identify the following quantities:
- The natural parameter
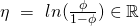 (and so
(and so 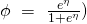
- The sufficient statistic
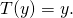 Matrix
Matrix 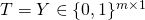 (here,
(here, 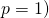
- The dispersion matrix is
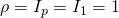
- The non-negative base measure is
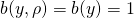
- The log-partition function maps
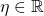 to:
to: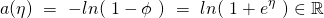
- The coefficient matrix is a row vector
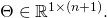
Step 3: The function ![]() maps
maps ![]() to
to ![]()
Step 4: If needed (e.g., in the case of NR algorithm), the function ![]() maps
maps ![]() to
to ![]()
![Rendered by QuickLaTeX.com \[ A_{\Theta} = \begin{bmatrix} ln(\ 1\ +\ e^{\Theta x^{(1)}\ })\\ ..\\ ln(\ 1\ +\ e^{\Theta x^{(m)}\ }) \end{bmatrix} \in \mathbb{R}^{m} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-532533e7ed25c6177f1cb4f64136f1e0_l3.png)
Step 6: The log-partition Gradient matrix is:
![]()
Step 7: If needed (e.g., in the case of NR algorithm), the second order diagonal matrix ![]() is given by:
is given by:
![Rendered by QuickLaTeX.com \[ (S_{11})_{\Theta} = \begin{bmatrix} \frac{e^{\Theta x^{(1)}}}{(1\ +\ e^{\Theta x^{(1)}})^{2}} & 0 & .. & 0 & 0\\ 0 & \frac{e^{\Theta x^{(2)}}}{(1\ +\ e^{\Theta x^{(2)}})^{2}} & .. & 0 & 0 \\ 0 & 0 & .. & 0 & 0\\ 0 & 0 & .. & 0 & \frac{e^{\Theta x^{(m)}}}{(1\ +\ e^{\Theta x^{(m)}})^{2}}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-6e3f06c50918054cc10148780a5f6006_l3.png)
Step 8: Compute the Cost Function ![]() , its Gradient
, its Gradient ![]() and its Hessian
and its Hessian ![]()
Step 9: Calculate the optimal ![]() using e.g., BGD, SGD, NR.
using e.g., BGD, SGD, NR.
Step 10: Test the model on an adequate test set and then conduct predictions on new input using the mean function ![]() (also known as the sigmoid function) that maps
(also known as the sigmoid function) that maps ![]() to:
to:
![]()
Note that:
![]()
![]()
Moreover, we know that:
![]()
As a result, we conclude that:
![]()
This is none else than the familiar logistic regression model where we predict ![]() whenever
whenever ![]() and
and ![]() otherwise. This classification highlights the presence of a decision boundary given by the set of inputs
otherwise. This classification highlights the presence of a decision boundary given by the set of inputs ![]() that satisfy
that satisfy ![]() This is justified by the fact that
This is justified by the fact that ![]()
iii. The Poisson distribution: The probability distribution with poisson rate ![]() is:
is:
![]()
The outcome ![]() is usually a count of an event occurrence. We can rewrite the distribution in an equivalent form that makes it easier to identify as a member of the exponential family:
is usually a count of an event occurrence. We can rewrite the distribution in an equivalent form that makes it easier to identify as a member of the exponential family:
![]()
Step 1: The target matrix ![]() In other terms, each training example
In other terms, each training example ![]() has a non-negative integer output
has a non-negative integer output ![]() associated with it.
associated with it.
Step 2: We identify the following quantities:
- The natural parameter
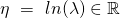 (and so
(and so 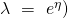
- The sufficient statistic
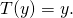 Matrix
Matrix 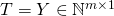 (here,
(here, 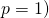
- The dispersion matrix is
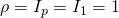
- The non-negative base measure is
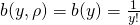
- The log-partition function maps
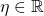 to:
to: 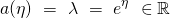
- The coefficient matrix is a row vector
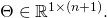
Step 3: The function ![]() maps
maps ![]() to
to ![]()
Step 4: If needed (e.g., in the case of NR algorithm), the function ![]() maps
maps ![]() to
to ![]()
Step 5: The log-partition vector is given by:
![Rendered by QuickLaTeX.com \[ A_{\Theta} = \begin{bmatrix} e^{\Theta x^{(1)}}\\ ..\\ e^{\Theta x^{(m)}}\ \end{bmatrix} \in \mathbb{R}^{m} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-82f2ea213586d44ec9e5c10da6d39ae8_l3.png)
Step 6: The log-partition Gradient matrix is:
![]()
Step 7: If needed (e.g., in the case of NR algorithm), The second order diagonal matrix ![]() is given by:
is given by:
![Rendered by QuickLaTeX.com \[ (S_{11})_{\Theta} = \begin{bmatrix} e^{\Theta x^{(1)}} & 0 & .. & 0 & 0\\ 0 & e^{\Theta x^{(2)}} & .. & 0 & 0 \\ 0 & 0 & .. & 0 & 0\\ 0 & 0 & .. & 0 & e^{\Theta x^{(m)}}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-6a06650032e5d1e4ca5b9ccb25cde0f3_l3.png)
Step 8: Evaluate the Cost Function ![]() , Gradient
, Gradient ![]() and Hessian
and Hessian ![]()
Step 9: Calculate optimal ![]() using e.g., BGD, SGD, NR.
using e.g., BGD, SGD, NR.
Step 10: Run the model on an adequate test set and then conduct predictions on new input using the mean function ![]() that maps
that maps ![]() to:
to:
![]()
Note that the range of ![]() is
is ![]() although the sufficient statistic is in
although the sufficient statistic is in ![]() This is because the mean function outputs the expected value of the sufficient statistic. So one would still need to map the expected value outputed by
This is because the mean function outputs the expected value of the sufficient statistic. So one would still need to map the expected value outputed by ![]() to an integer in
to an integer in ![]()
iv. The Geometric distribution: The corresponding probability distribution is:
![]()
The outcome ![]() is
is ![]() The distribution calculates the probability of having a success after exactly
The distribution calculates the probability of having a success after exactly ![]() trials, where the probability of success is equal to
trials, where the probability of success is equal to ![]() We rewrite it in an equivalent form that makes it easier to identify as a member of the exponential family:
We rewrite it in an equivalent form that makes it easier to identify as a member of the exponential family:
![]()
Step 1: The target matrix ![]() In other terms, each training example
In other terms, each training example ![]() has a positive integer output
has a positive integer output ![]() associated with it.
associated with it.
Step 2: We identify the following quantities:
- The natural parameter
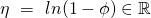 (and so
(and so 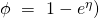
- The sufficient statistic
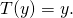 Matrix
Matrix 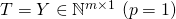
- The dispersion matrix is
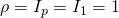
- The non-negative base measure is
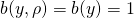
- The log-partition function maps
 to:
to:
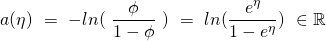
- The coefficient matrix is a row vector
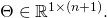
Step 3: The map ![]() takes
takes ![]() to
to ![]()
Step 4: In case required (e.g., in the case of NR algorithm), the function ![]() maps
maps ![]() to
to ![]()
Step 5: Derive the log-partition vector:
![Rendered by QuickLaTeX.com \[ A_{\Theta} = \begin{bmatrix} ln(\ \frac{e^{\Theta x^{(1)}}}{(\ 1\ -\ e^{\Theta x^{(1)}}\ )}\ )\\ ..\\ ln(\ \frac{e^{\Theta x^{(m)}}}{(\ 1\ -\ e^{\Theta x^{(m)}}\ )}\ ) \end{bmatrix} \in \mathbb{R}^{m} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e58aba6ca587c8c28db70c590098a2bc_l3.png)
Step 6: The log-partition Gradient matrix is:
![Rendered by QuickLaTeX.com \begin{equation*} D_{\Theta}\ =\ [\ \frac{1}{1\ -\ e^{\Theta x^{(1)}}}\ \ ..\ \ \frac{1}{1\ -\ e^{\Theta x^{(m)}}}\ ] \in \mathbb{R}^{1 \times m} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-2f2c4a994f7d9b96ff8b070bbd11844c_l3.png)
Step 7: If needed (e.g., in the case of NR algorithm), the second order diagonal matrix ![]() is given by:
is given by:
![Rendered by QuickLaTeX.com \[ (S_{11})_{\Theta} = \begin{bmatrix} \frac{e^{\Theta x^{(1)}}}{(1\ -\ e^{\Theta x^{(1)}})^{2}} & 0 & .. & 0 & 0\\ 0 & \frac{e^{\Theta x^{(2)}}}{(1\ -\ e^{\Theta x^{(2)}})^{2}} & .. & 0 & 0 \\ 0 & 0 & .. & 0 & 0\\ 0 & 0 & .. & 0 & \frac{e^{\Theta x^{(m)}}}{(1\ -\ e^{\Theta x^{(m)}})^{2}}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-b6461232081f1b2bc32e4fa9dc65dade_l3.png)
Step 8: Evaluate the Cost Function ![]() , Gradient
, Gradient ![]() and Hessian
and Hessian ![]()
Step 9: Evaluate the optimal ![]() using e.g., BGD, SGD, NR.
using e.g., BGD, SGD, NR.
Step 10: Run the model on a test set and conduct predictions on new input using the mean function ![]() that maps
that maps ![]() to:
to:
![]()
Note that the range of ![]() is
is ![]() although the sufficient statistic is in
although the sufficient statistic is in ![]() This is because the mean function outputs the expected value of the sufficient statistic. So one would still need to map the expected value outputed by
This is because the mean function outputs the expected value of the sufficient statistic. So one would still need to map the expected value outputed by ![]() to an integer in
to an integer in ![]()
v. The Multinomial distribution: The corresponding probability distribution is:
![]()
Here, ![]() is a function of
is a function of ![]() that returns 1 if and only if
that returns 1 if and only if ![]() and returns 0 otherwise. One can think of this distribution as the probability of
and returns 0 otherwise. One can think of this distribution as the probability of ![]() taking a value in the set
taking a value in the set ![]() with:
with:
![]()
…
![]()
![]()
We rewrite it in an equivalent form that makes it easier to identify as a member of the exponential family:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} p(y;\ \phi_{1}, ..., \phi_{k-1})\ =\ e^{\ ln\ [\ \Pi_{i=1}^{k-1}\ \phi_{i}^{1\{y=i\}}\ (\ 1 - \Sigma_{j=1}^{k-1}\ \phi_{j}\ )^{1\{y=k\}}\ ]}\ = \\ \\ e^{[\ \Sigma_{i=1}^{k-1}\ 1\{y=i\}\ ln(\phi_{i})\ +\ 1\{y=k\}\ ln(\ 1 - \Sigma_{j=1}^{k-1}\ \phi_{j}\ )\ ]}\ = \\ \\ e^{[\ \Sigma_{i=1}^{k-1}\ 1\{y=i\}\ ln(\phi_{i})\ +\ (\ 1 - \Sigma_{i=1}^{k-1}\ 1\{y=i\}\ )\ ln(\ 1 - \Sigma_{j=1}^{k-1}\ \phi_{j}\ )\ ]}\ = \\ \\ e^{[\ \Sigma_{i=1}^{k-1}\ 1\{y=i\}\ ln(\frac{\phi_{i}}{(\ 1 - \Sigma_{j=1}^{k-1}\ \phi_{j}\ )})\ +\ ln(\ 1 - \Sigma_{j=1}^{k-1}\ \phi_{j}\ )\ ]} \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-64a593dfd5f78ad3deb60fc88efe821f_l3.png)
Step 1: The target matrix ![]() In other terms, each training example
In other terms, each training example ![]() has an integer output
has an integer output ![]() associated with it.
associated with it.
Step 2: We identify the following quantities:
- The natural parameter is given by:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} \eta \equiv [\eta_{1}\ ...\ \eta_{k-1}]^{T}\ =\\ \\ [\ ln(\frac{\phi_{1}}{(\ 1 - \Sigma_{j=1}^{k-1}\ \phi_{j})}\ )\ \ ..\ \ ln(\frac{\phi_{k-1}}{(\ 1 - \Sigma_{j=1}^{k-1}\ \phi_{j})}\ )\ ]^{T} \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-b2e9e8a75cd766af7298d08186818dd0_l3.png)
- The sufficient statistic of
 is:
is: ![Rendered by QuickLaTeX.com \begin{equation*} T(y) = [\ 1\{y=1\}\ \ ..\ \ 1\{y=k-1\}\ ]^{T} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-545a5b5180c1de7febfacc120c6f5253_l3.png)
As a result, the sufficient statistic matrix is given by:
![Rendered by QuickLaTeX.com \[ T = \begin{bmatrix} 1\{y^{(1)}=1\} & .. & 1\{y^{(1)} = (k-1)\}\\ .. & .. & ..\\ 1\{y^{(m)}=1\} & .. & 1\{y^{(m)} = (k-1)\}\\ \end{bmatrix} \in \{0,1\}^{m \times (k-1)}\ \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-41e934c13aa35ae7ca14b0c051de38b4_l3.png)
Here,
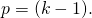
- The dispersion matrix is
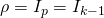
- The non-negative base measure is
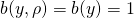
- The log-partition function maps
 to:
to: 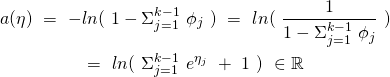
- The coefficient matrix is given by:
![Rendered by QuickLaTeX.com \[ \Theta = \begin{bmatrix} \Theta_{1}^{T}\\ .. \\ \Theta_{(k-1)}^{T}\\ \end{bmatrix} = \begin{bmatrix} \theta_{11} & .. & \ \theta_{1(n+1)}\\ .. & .. & ..\\ \theta_{(k-1)1} & .. & \ \theta_{(k-1)(n+1)}\\ \end{bmatrix} \in \mathbb{R}^{(k-1) \times (n+1)} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-5995e2c09cc626c80054c8d24e33a140_l3.png)
Step 3: ![]() the function
the function ![]() corresponds to the following mapping:
corresponds to the following mapping:
![]()
Step 4: If needed (e.g., in the case of NR algorithm), ![]() the function
the function ![]() can be computed as follows:
can be computed as follows:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} \eta\ \equiv\ [\eta_{1}\ ...\ \eta_{k-1}]^{T}\ \rightarrow\\ \frac{1}{(\ 1\ +\ \Sigma_{j=1}^{k-1}\ e^{\eta_{j}}\ )^{2}}\ [\ \delta_{st}\ e^{\eta_{t}}\ (\ 1\ +\ \Sigma_{j=1}^{k-1}\ e^{\eta_{j}}\ )\ -\ e^{[\ \eta_{s}\ +\ \eta_{t}\ ]}\ ] \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-54ace455a7c8da3bce0d5fb5fa30c2bc_l3.png)
where ![]() if
if ![]() and
and ![]() otherwise.
otherwise.
Step 5: We evaluate the log-partition vector to be:
![Rendered by QuickLaTeX.com \[ A_{\Theta} = \begin{bmatrix} ln(\ 1\ +\ \Sigma_{j=1}^{k-1}\ e^{\Theta_{j}^{T} x^{(1)}}\ )\\ ..\\ ln(\ 1\ +\ \Sigma_{j=1}^{k-1}\ e^{\Theta_{j}^{T} x^{(m)}}\ )\\ \end{bmatrix} \in \mathbb{R}^{m} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-b7d78c72faf7d547b485007a373bf741_l3.png)
Step 6: The log-partition Gradient matrix is given by:
![Rendered by QuickLaTeX.com \[ D_{\Theta} = \begin{bmatrix} \frac{e^{[\Theta_{1}^{T} x^{(1)}]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{T} x^{(1)}]}} & .. & .. & \frac{e^{[\Theta_{1}^{T} x^{(m)}]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{T} x^{(m)}]}}\\ .. & .. & .. & ..\\ .. & .. & .. & ..\\ \frac{e^{[\Theta_{k-1}^{T} x^{(1)}]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{T} x^{(1)}]}} & .. & .. & \frac{e^{[\Theta_{k-1}^{T} x^{(m)}]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{k-1}^{T} x^{(m)}]}}\\ \end{bmatrix} \in \mathbb{R}^{(k-1) \times m} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-53c509ae5b4f8da369bc2d7f13e97b58_l3.png)
Step 7: If needed (e.g., in the case of NR algorithm), ![]() the second order diagonal matrix
the second order diagonal matrix ![]() is the diagonal matrix whose
is the diagonal matrix whose ![]() entry (
entry (![]() ) is given by:
) is given by:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} (\ (S_{uv})_{\Theta}\ )_{ii} = \frac{1}{(\ 1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{T} x^{(i)}]}\ )^{2}}\ \times\\ \\ [\ \delta_{uv}\ (\ 1\ +\ \Sigma_{j=1}^{k-1}\ e^{\Theta_{j}^{T} x^{(i)}}\ )\ e^{\Theta_{v}^{T} x^{(i)}}\ -\ e^{[\ (\Theta_{u}^{T} + \Theta_{v}^{T}) x^{(i)}\ ]}] \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-e51ef9909cf6dd402ae8079d0cc489d2_l3.png)
Step 8: Calculate the Cost Function ![]() , its Gradient
, its Gradient ![]() and its Hessian
and its Hessian ![]()
Step 9: Compute the optimal ![]() using e.g., BGD, SGD, NR.
using e.g., BGD, SGD, NR.
Step 10: Test the model on a test set and then conduct predictions on new input using the mean function ![]() that maps
that maps ![]() to:
to:
![Rendered by QuickLaTeX.com \[ h(\eta)\ =\ (\bigtriangledown_{\eta}\ a)^{T}\ (\Theta^{*}\ x)\ = \begin{bmatrix} \frac{e^{[\Theta_{1}^{*T}\ x]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{*T}\ x]}}\\ \\ ..\\ \\ \frac{e^{[\Theta_{k-1}^{*T}\ x]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{*T}\ x]}}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-88a0802e1eb1153487ddcc9dd4fb3358_l3.png)
Note that by definition, we have ![]() Substituting the previously derived expression for
Substituting the previously derived expression for ![]() we get:
we get:
![Rendered by QuickLaTeX.com \[ \begin{bmatrix} E[\ 1\{y=1\}\ |\ x;\ \Theta]\\ \\ \\ ..\\ \\ \\ E[\ 1\{y=k-1\}\ |\ x;\ \Theta] \end{bmatrix} = \begin{bmatrix} \frac{e^{[\Theta_{1}^{*T}\ x]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{*T}\ x]}}\\ \\ ..\\ \\ \frac{e^{[\Theta_{k-1}^{*T}\ x]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{*T}\ x]}}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-ff6db88113469f3fcba5b902d82cb770_l3.png)
Observing that
![]()
We get ![]()
![Rendered by QuickLaTeX.com \[ \begin{bmatrix} \\ \phi_{1} \\ \\ .. \\ \\ \phi_{k-1} \\ \\ \end{bmatrix} \equiv \begin{bmatrix} \\ p(y=1\ |\ x;\ \Theta) \\ \\ .. \\ \\ p(y=(k-1)\ |\ x;\ \Theta) \\ \\ \end{bmatrix} = \begin{bmatrix} \frac{e^{[\Theta_{1}^{*T}\ x]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{*T}\ x]}}\\ \\ ..\\ \\ \frac{e^{[\Theta_{k-1}^{*T}\ x]}}{1\ +\ \Sigma_{j=1}^{k-1}\ e^{[\Theta_{j}^{*T}\ x]}}\\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-b8b974c570cf320380352a6451ca4f92_l3.png)
This is the familiar softmax regression model. We predict ![]() whenever
whenever ![]() and where we define
and where we define ![]() to be equal to
to be equal to ![]() This classification highlights the presence of decision boundaries that delimit
This classification highlights the presence of decision boundaries that delimit ![]() distinct zones where the
distinct zones where the ![]() zone correspond to the set of
zone correspond to the set of ![]() vectors for which
vectors for which ![]() .
.
Note that logistic regression is a special case of softmax regression when ![]()
7. The multivariate Gaussian distribution case
The multivariate Gaussian distribution is given by:
![]()
where ![]() and
and ![]() is a symmetric positive definite matrix in
is a symmetric positive definite matrix in ![]()
Note that the symmetry and positive definiteness of ![]() imply the symmetry and positive definiteness of
imply the symmetry and positive definiteness of ![]() as we now demonstrate.
as we now demonstrate.
- Proof that
 is symmetric: We claim that for any invertible matrix
is symmetric: We claim that for any invertible matrix 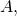 it holds that
it holds that 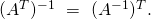 Indeed, letting
Indeed, letting  denote the identity matrix, we have the following chain of equalities:
denote the identity matrix, we have the following chain of equalities:
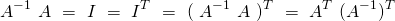
It ensues that
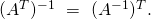 By virtue of being positive definite,
By virtue of being positive definite,  is invertible and we get as a result that
is invertible and we get as a result that 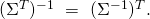 Invoking the symmetric nature of
Invoking the symmetric nature of  we then conclude that
we then conclude that 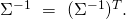 This shows that
This shows that 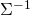 is symmetric.
is symmetric. - Proof that
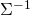 is positive definite: Being positive definite,
is positive definite: Being positive definite, 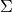 exclusively admits positive eigenvalues. But the eigenvalues of
exclusively admits positive eigenvalues. But the eigenvalues of 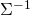 are the reciprocals of those of
are the reciprocals of those of 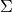 and hence are also positive. This in turn implies that
and hence are also positive. This in turn implies that 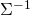 is positive definite.
is positive definite.
We rewrite the probability distribution in an equivalent form that makes it easier to identify as a member of the exponential family with dispersion matrix:
![]()
![]()
Being a scalar, the quantity ![]() is equal to its transpose
is equal to its transpose ![]() And since
And since ![]() is symmetric, it must be that
is symmetric, it must be that ![]() Moreover, the determinant of
Moreover, the determinant of ![]() satisfies
satisfies ![]() As a result, we write:
As a result, we write:
![]()
![Rendered by QuickLaTeX.com \begin{equation*} \sqrt{\frac{\left| {\Sigma^{-1}} \right| }{(2 \pi)^{r}}}\ e^{-\frac{1}{2}\ (y^{T}\ \Sigma^{-1}\ y)}\ e^{[\ (\mu^{T}\ \Sigma^{-1}\ y)\ -\ \frac{1}{2}\ (\mu^{T}\ \Sigma^{-1}\ \mu)\ ]} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-1c0c1fe77b21716d686f93d57a4ed0a4_l3.png)
Step 1: The target matrix ![]() In other terms, each training example
In other terms, each training example ![]() has a multivariate output
has a multivariate output ![]() associated with it.
associated with it.
Step 2: We identify the following quantities:
- The natural parameter vector
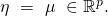
- The sufficient statistic
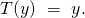 Matrix
Matrix  Note that the dimension
Note that the dimension  of the sufficient statistic is equal to the dimension
of the sufficient statistic is equal to the dimension  of
of 
- The dispersion matrix is
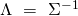 which is not necessarily a positive multiple of the identity matrix
which is not necessarily a positive multiple of the identity matrix 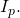 The inverse of the covariance matrix
The inverse of the covariance matrix  is also usually known as the precision matrix.
is also usually known as the precision matrix. - The non-negative base measure is:
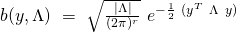
- The log-partition function maps
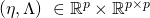 to:
to: 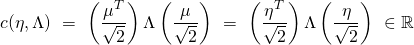
where
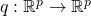 is the map that takes
is the map that takes ![Rendered by QuickLaTeX.com \eta\ \equiv\ [\eta_{1}\ ..\ \eta_{p}]^{T}](https://delfr.com/wp-content/ql-cache/quicklatex.com-575e489e204a47f143aa7f9b0339bc0f_l3.png) to
to 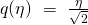
We can also compute the derivative of
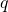 with respect to
with respect to 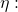
![Rendered by QuickLaTeX.com \[ (\mathcal{D}_{\eta}\ q)\ =\ \begin{bmatrix} \frac{\partial q_{1}}{\partial \eta_{1}} & .. & \frac{\partial q_{1}}{\partial \eta_{p}}\\ .. & .. & ..\\ \frac{\partial q_{p}}{\partial \eta_{1}} & .. & \frac{\partial q_{p}}{\partial \eta_{p}} \end{bmatrix} (\eta)\ = \frac{1}{\sqrt{2}}\ I_{p} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-07456da97561f876ee2c21e50ea567b9_l3.png)
- The coefficient matrix is
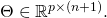
Step 3: We claim that the Gradient of ![]() with respect to
with respect to ![]() is the map from
is the map from ![]() to
to ![]() that takes
that takes ![]() to
to ![]()
To see why, note that if ![]() is a given matrix and
is a given matrix and ![]() maps vector
maps vector ![]() to
to ![]() then
then
![]()
As a result, ![]()
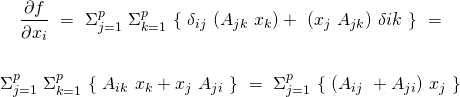
And so: ![]()
We then conclude that: ![]()
Step 4: We now turn to computing the cost function ![]() derived from conducting maximum likelihood estimation using the multivariate Gaussian distribution. After substituting the relevant parameters in equation
derived from conducting maximum likelihood estimation using the multivariate Gaussian distribution. After substituting the relevant parameters in equation ![]() we get:
we get:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} J^{(LG)}_{x, \lambda}(\Theta, \Lambda)\ =\ \frac{1}{m}\ \Sigma_{i=1}^{m}\ w^{(i)}_{x}\ \{\ \frac{1}{2}\ (x^{(i)})^{T}\ \Theta^{T}\ \Lambda\ \Theta\ x^{(i)}\ -\\ (x^{(i)})^{T}\ \Theta^{T}\ \Lambda\ y^{(i)}\ +\ \frac{1}{2}\ (y^{(i)})^{T}\ \Lambda\ y^{(i)}\ +\ \frac{1}{2}\ ln(\ (2 \pi)^{p}\ \left| {\Lambda^{-1}} \right|\ )\ \}\ +\\ \frac{\lambda}{2}\ \Sigma_{j=1}^{p}\ [\ \Theta_{j}^{T}\ \Theta_{j}\ +\Lambda_{j}^{T}\ \Lambda_{j}\ ] \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-cfc0d05df8125ee405f5c562403f32fa_l3.png)
We rewrite this more concisely using matrix notation as follows:
(32) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed { \begin{gathered} J^{(LG)}_{x, \lambda} (\Theta, \Lambda)\ =\\ \frac{1}{m}\ Tr \{\ [\ \frac{1}{2}\ X\ \Theta^{T} \Lambda\ \Theta\ X^{T}\ -\ X\ \Theta^{T} \Lambda\ Y^{T}\ +\\ \frac{1}{2}\ Y\ \Lambda\ Y^{T}\ +\ \frac{1}{2}\ ln(\ (2 \pi)^{p}\ \left| {\Lambda^{-1}} \right|\ )\ I_{p}\ ]\ W_{x}\ \}\ +\\ \frac{\lambda}{2}\ [\ Tr(\Theta\ \Theta^{T})\ +\ Tr(\Lambda\ \Lambda^{T})\ ] \end{gathered} } \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-13457a7ebed922f120ee56aeab278805_l3.png)
We have seen earlier that the long form general Cost Function is convex in ![]() Moreover, we showed that if
Moreover, we showed that if ![]() is convex in
is convex in ![]() then so will the Cost Function. We now demonstrate that for the case of the multivariate Gaussian,
then so will the Cost Function. We now demonstrate that for the case of the multivariate Gaussian, ![]() is indeed convex in
is indeed convex in ![]() To do so, we prove the equivalent claim that
To do so, we prove the equivalent claim that ![]() is convex in
is convex in ![]() To see why, note that:
To see why, note that:
![]()
Note that the first term is linear in ![]() and hence convex in
and hence convex in ![]() The last term is independent of
The last term is independent of ![]() The second term is a negative multiple of the natural logarithm of the determinant of a positive definite matrix. To establish the convexity of this quantity, we first find the Gradient of
The second term is a negative multiple of the natural logarithm of the determinant of a positive definite matrix. To establish the convexity of this quantity, we first find the Gradient of ![]() which turns out to be equal to
which turns out to be equal to ![]() (for a proof, the reader can refer to e.g., section 4.A.1 of [1]). We then compute the Hessian which turns out to be equal to
(for a proof, the reader can refer to e.g., section 4.A.1 of [1]). We then compute the Hessian which turns out to be equal to ![]() This shows that the Hessian is positive definite which implies that
This shows that the Hessian is positive definite which implies that ![]() is convex in
is convex in ![]()
Step 5: We now turn to computing the Cost Function’s Gradient as specified by equation ![]() In order to do so, we first prove some identities involving the derivative of a Trace.
In order to do so, we first prove some identities involving the derivative of a Trace.
- Gradient of
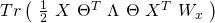 :
: In what follows, the quantity
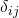 evaluates to 1 if
evaluates to 1 if  and 0 otherwise. First of all, note that:
and 0 otherwise. First of all, note that: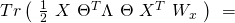
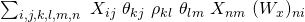
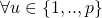 and
and  we can express the
we can express the  component of its derivative with respect to
component of its derivative with respect to 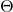 as follows:
as follows:![Rendered by QuickLaTeX.com \begin{equation*} \begin{gathered} \left [\ \bigtriangledown_{\Theta}\ \ Tr \left (\ \frac{1}{2}\ X\ \Theta^{T}\ \Lambda\ \Theta\ X^{T}\ W_{x}\ \right )\ \right ]_{uv}\ = \\ \\ \frac{1}{2}\ \frac{\partial }{\partial \theta_{uv}} \sum_{i,j,k,l,m,n}\ X_{ij}\ \theta_{kj}\ \rho_{kl}\ \theta_{lm}\ X_{nm}\ (W_{x})_{ni}\ = \\ \\ \frac{1}{2}\ \sum_{i,j,k,l,m,n} [\ X_{ij}\ \delta_{uk}\ \delta_{vj}\ \rho_{kl}\ \theta_{lm}\ X_{nm}\ (W_x)_{ni}\\ +\ \ X_{ij}\ \theta_{kj}\ \rho_{kl}\ \delta_{ul}\ \delta_{vm}\ X_{nm}\ (W_x)_{ni}\ ]\ = \\ \\ \frac{1}{2}\ \sum_{i,j,k,l,m,n}[\ X_{iv}\ \rho_{ul}\ \theta_{lm}\ X_{nm}\ (W_x)_{ni}\\ +\ \ X_{ij}\ \theta_{kj}\ \rho_{ku}\ X_{nv}\ (W_x)_{ni}\ ]\ = \\ \\ \frac{1}{2}\ \sum_{i,j,k,l,m,n}[\ \rho_{ul}\ \theta_{lm}\ X_{nm}\ (W_x)_{ni}\ X_{iv}\\ +\ \ \rho_{ku}\ \theta_{kj}\ X_{ij}\ (W_x)_{ni}\ X_{nv}\ ]\ = \\ \\ \frac{1}{2} \left (\ \Lambda\ \Theta\ X^{T}\ W_{x}\ X\ \right )_{uv}\ +\ \frac{1}{2} \left (\ \Lambda^{T}\ \Theta\ X^{T}\ W_{x}^{T}\ X\ \right )_{uv}\ = \\ \\ (\ \Lambda\ \Theta\ X^{T}\ W_{x}\ X\ )_{uv} \end{gathered} \end{equation*}](https://delfr.com/wp-content/ql-cache/quicklatex.com-ed591154f4e7e80dcfb87b73883782f9_l3.png)
(since
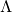 and
and 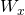 are symmetric.)
are symmetric.)As a result, we conclude that:
(33)
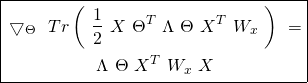
Similarly, we can follow the same procedure to find that:
(34)
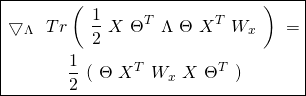
-
Gradient of
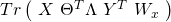 :
:We first notice that:
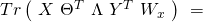
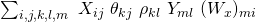
Since
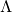 is symmetric, we can equivalently write this equality as:
is symmetric, we can equivalently write this equality as: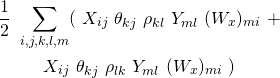
We then apply the same logic as before and demonstrate that:
(35)
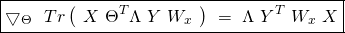
And that:
(36)
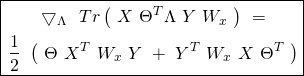
-
Gradient of
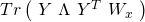 :
:Given the lack of dependency on
 it is obvious that:
it is obvious that:(37)
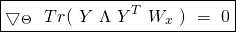
Furthermore, observing that
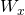 is symmetric and applying the same methodology that we previously used allow us to readily show that:
is symmetric and applying the same methodology that we previously used allow us to readily show that:(38)
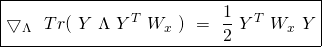
-
Gradient of
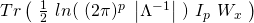 :}
:}Here too, independence of
 justifies that:
justifies that:(39)
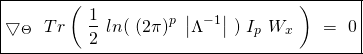
On the other hand, we have:
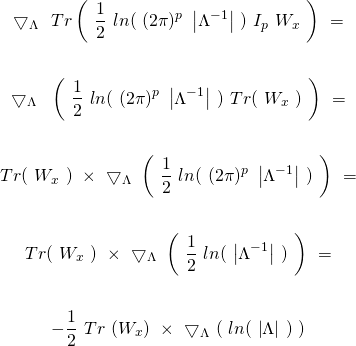
We stated earlier that
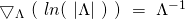 (see e.g., section 4.A.1 of [1]). As a result, we conclude that:
(see e.g., section 4.A.1 of [1]). As a result, we conclude that:(40)
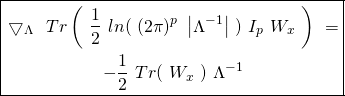
-
Gradient of
 and
and 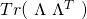 :}
:}Clearly:
(41)
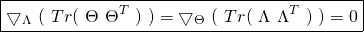
Furthermore, we can apply the same calculation as before to conclude that:
(42)
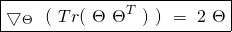
(43)
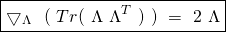
The Gradient of the Cost Function can now be readily computed as:
(44) 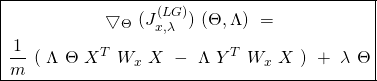
(45) 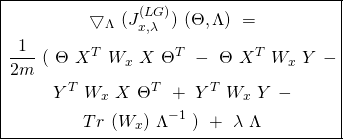
Step 6: With the Cost function and its gradient thus derived, we can use numerical algorithms to find the optimal ![]() and
and ![]() that minimize
that minimize ![]() In what follows we illustrate how this can be done using BGD. Recall that
In what follows we illustrate how this can be done using BGD. Recall that ![]() denotes the learning rate matrix that was previously introduced in section 5, iter is an iteration count variable and max-iter is the maximum number of allowed iterations before testing for convergence:
denotes the learning rate matrix that was previously introduced in section 5, iter is an iteration count variable and max-iter is the maximum number of allowed iterations before testing for convergence:
![]()
![]()
(They could be initialized to e.g., and
respectively).
For (iter ![]() max-iter)
max-iter)
![]()
![]()
![]()
![]()
![]()
Update all the ![]() and
and ![]() -dependent quantities including:
-dependent quantities including:
![]()
![]()
![]()
![]()
It is important to note that the entries of matrices ![]() and
and ![]() must get simultaneously updated before they can be used in the next iteration.
must get simultaneously updated before they can be used in the next iteration.
Step 7 Test the model on an adequate test set and then conduct predictions on new input using the mean function ![]() that maps
that maps ![]() to:
to:
![]()
It turns out that one can calculate the optimal coefficient matrix ![]() and the optimal dispersion matrix
and the optimal dispersion matrix ![]() in closed form whenever the Cost Function is expressed in its long basic form
in closed form whenever the Cost Function is expressed in its long basic form ![]() . In other terms, whenever we assume that the weight matrix
. In other terms, whenever we assume that the weight matrix ![]() is independent of
is independent of ![]() and equal to the
and equal to the ![]() identity matrix, and that the regularization matrix is independent of
identity matrix, and that the regularization matrix is independent of ![]() and equal to the
and equal to the ![]() 0 matrix. In this case, equation
0 matrix. In this case, equation ![]() yields:
yields:
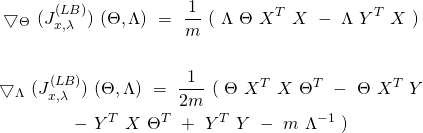
Recall that the Cost Function is convex in ![]() and in
and in ![]() We can therefore find
We can therefore find ![]() and
and ![]() by setting the Gradient with respect to
by setting the Gradient with respect to ![]() and to
and to ![]() to 0. By doing so, we get:
to 0. By doing so, we get:
![]()
Since ![]() is positive definite, this is equivalent to
is positive definite, this is equivalent to ![]() We then retrieve the familiar normal equation we obtained in the univariate case:
We then retrieve the familiar normal equation we obtained in the univariate case:
![]()
Similarly, by setting ![]() we find:
we find:
![]()
8. Python implementation
This section provides a python script that implements the Generalized Linear Model Supervised Learning class using matrix notation. We limit ourselves to cases where the dispersion matrix is a positive scalar multiple of the identity matrix. We emphasize that the code is meant for educational purposes and we recommend using tested packages (e.g., Scikit-Learn) to run specific predictive models.
import sys;
import math;
import numpy as np;
# THE GLM CLASS DEFINES AN INSTANCE OF A PREDICTION PROBLEM.
# IN ORDER TO DEFINE AN INSTANCE, ONE SHOULD PROVIDE THE FOLLOWING:
# -----------------------------------------------------------------------
# ------X_train (m by (n+1)): Training set input (including all-1 column)
# --------------------------- m is number of training examples and n is
# --------------------------- number of features.
# -----------------------------------------------------------------------
# ------Y_train (m by r): Output matrix for the training set.
# --------------------------- m is number of training examples and r is
# --------------------------- the output's dimension.
# -----------------------------------------------------------------------
# ------reg_model: String defining the probability distribution to be
# --------------------------- used for regression / classification. We
# --------------------------- include the following (but can be expanded
# --------------------------- further): "normal", "binomial", "poisson",
# --------------------------- "geometric", "multinomial".
# -----------------------------------------------------------------------
# ------p: Refers to the dimension of the sufficient stastic. For most
# --------------------------- examples used here, it is equal to 1. For
# --------------------------- multinomial classification it is equal to
# --------------------------- one less than the number of classes.
# -----------------------------------------------------------------------
# ------regu_lambda: Refers to the regularization parameter lambda. it is
# --------------------------- a scalar that can be set to 0.
# -----------------------------------------------------------------------
# ------weight_flag: Should be set to 1 if one wishes to conduct weighted
# --------------------------- regression/ classification. It relies on
# --------------------------- the familiar bell-shaped function. In this
# --------------------------- case, the data point where prediction is to
# --------------------------- be made defines the weights to be used. As
# --------------------------- a result, that specific data point must be
# --------------------------- included as an input to the fitting process
# --------------------------- as we later describe in the "fit" method.
# --------------------------- If no weights are needed, set flag to 0.
# -----------------------------------------------------------------------
# ------weight_tau: Holds the bandwidth value tau of the weight function.
# --------------------------- It is set to 1 by default and is only used
# --------------------------- when the weight_flag is set to 1.
# -----------------------------------------------------------------------
class Glm:
def __init__(self, X_train, Y_train, reg_model, p, regu_lambda,
weight_flag, weight_tau = 1):
self.X_train = X_train
self.Y_train = Y_train
self.reg_model = reg_model
self.p = p
self.regu_lambda = regu_lambda
self.weight_flag = weight_flag
self.weight_tau = weight_tau
def display_X_train(self):
print "\n The training set input matrix is:\n", self.X_train
def display_Y_train(self):
print "\n The training set output is:\n", self.Y_train
def display_reg_model(self):
print "\n The model is a: ", self.reg_model, " distribution"
def display_regu_lambda(self):
print "\n The regularization parameter is: ", self.regu_lambda
def display_weight_flag(self):
if (self.weight_flag == 1):
print "\n The current prediction instance is weighted"
elif (self.weight_flag == 0):
print "\n The current prediction instance is not weighted"
else: print "\n Flag value not recognized. Please insert 1 or 0"
def display_weight_tau(self):
if (self.weight_flag == 1):
print "\n The weight function bandwidth is ", self.weight_tau
else: print "\n The current prediction is not weighted."
# THE GLM CLASS INCLUDES 3 GETTER METHODS. THESE ARE:
# ------get_m(): Returns total number of training examples.
# -----------------------------------------------------------------------
# ------get_n(): Returns total number of input features. We subtract 1
# --------------------------- to exclude X_train's all-1 column.
# -----------------------------------------------------------------------
# ------get_p(): Returns dimension of the sufficient statistic.
# -----------------------------------------------------------------------
def get_m(self):
return self.X_train.shape[0]
def get_n(self):
return self.X_train.shape[1] - 1
def get_p(self):
return self.p
# THE GLM CLASS LEVERAGES MATRIX NOTATION. THE FOLLOWING METHODS HELP
# GENERATE THE RELEVANT MATRICIAL QUANTITIES.
# ------weight_bell_func(x, training_i): Returns the weight specific
# --------------------------- to training example i, as dictated by input
# --------------------------- x (which is an (n+1) by 1 vector). The
# --------------------------- The weight we use is the bell-shaped one
# --------------------------- with bandwidth tau.
# -----------------------------------------------------------------------
# ------generate_W(x): Generates the weight matrix W associated with
# --------------------------- input x. When the weighted regression flag
# --------------------------- is 0, it is the (m by m) identity matrix.
# -----------------------------------------------------------------------
# ------generate_L(): Generates the ((n+1) by (n+1)) regularization
# --------------------------- matrix L. It is equal to "lambda" times the
# --------------------------- ((n+1) by (n+1)) identity matrix.
# -----------------------------------------------------------------------
# ------generate_T(): Generates the (m by p) sufficient statistic matrix
# --------------------------- T. It depends on the probabilistic model.
# --------------------------- Note that for the multinomial model, we
# --------------------------- label classes from 0 to (p-1).
# -----------------------------------------------------------------------
def weight_bell_func(self, x, training_i):
return math.exp(-np.dot((self.X_train[training_i,::] - x.T),
(self.X_train[training_i,::] - x.T).T)/
float(2*(self.weight_tau**2)))
def generate_W(self, x):
m = self.get_m()
W = np.eye(m, dtype=np.float64)
if (self.weight_flag == 1):
for i in range(m):
W[i,i] = self.weight_bell_func(x, i)
return W
def generate_L(self):
n = self.get_n()
L = self.regu_lambda * np.eye(n+1, dtype=np.float64)
return L
def generate_T(self):
p = self.get_p()
m = self.get_m()
T = np.zeros((m,p), dtype=np.float64)
if (self.reg_model in ["normal", "binomial", "poisson",
"geometric"]):
T = self.Y_train
elif (self.reg_model == "multinomial"):
for i in range(m):
for j in range(p):
if(int(self.Y_train[i,0]) == j):
T[i,j] = 1
else:
print "No valid model has been inserted. System exiting now"
sys.exit()
return T
# TO GENERATE THE REMAINING RELEVANT MATRICES, THE GLM CLASS MAKES USE OF
# QUANTITIES BUILT OFF THE LOG-PARTITION FUNCTION AND ITS DERIVATIVES.
# THE LOG-PARTITION FUNCTION IS PROBABILITY DISTRIBUTION-DEPENDENT.
# ------a_func(eta): Returns the value of the relevant log-partition
# --------------------------- function evaluated at eta. For most of the
# --------------------------- encoded distributions, the first derivative
# --------------------------- is a function from R to R. For the case of
# --------------------------- the multinomial, it is a map from R^p to R.
# -----------------------------------------------------------------------
# ------a_first_deriv(eta, index): Returns the value of the partial
# --------------------------- derivative of the log-partition function
# --------------------------- with respect to the index's variable and
# --------------------------- evaluated at eta. For most of the encoded
# --------------------------- distributions, the first derivative is a
# --------------------------- function from R to R. For the case of the
# --------------------------- multinomial, it is a map from R^p to R.
# -----------------------------------------------------------------------
# ------a_second_deriv(eta, index1, index2): Returns the value of the 2nd
# --------------------------- partial derivative of the log-partition
# --------------------------- function with respect to the 2 indexes'
# --------------------------- variables index1 and index2 evaluated at
# --------------------------- eta. For most of the encoded distributions,
# --------------------------- the second derivative is a function from R
# --------------------------- to R. For the case of the multinomial, it
# --------------------------- is a function from R^p to R.
# -----------------------------------------------------------------------
def a_func(self, eta):
p = self.get_p()
if (self.reg_model == "normal"):
return eta**2/float(2)
elif (self.reg_model == "binomial"):
return math.log(1+math.exp(eta))
elif (self.reg_model == "poisson"):
return math.exp(eta)
elif (self.reg_model == "geometric"):
return math.log(math.exp(eta)/float(1-math.exp(eta)))
elif (self.reg_model == "multinomial"):
val = 0
for j in range(p):
val += math.exp(eta[j])
return math.log(val + 1)
else:
print "No valid model has been inserted. System exiting now"
sys.exit()
def a_first_deriv(self, eta, index):
p = self.get_p()
if (self.reg_model == "normal"):
return eta
elif (self.reg_model == "binomial"):
return math.exp(eta)/float(1+math.exp(eta))
elif (self.reg_model == "poisson"):
return math.exp(eta)
elif (self.reg_model == "geometric"):
return 1/float(1-math.exp(eta))
elif (self.reg_model == "multinomial"):
denom = 1
for j in range(p):
denom += math.exp(eta[j])
return math.exp(eta[index])/float(denom)
else:
print "No valid model has been inserted. System exiting now"
sys.exit()
def a_second_deriv(self, eta, index1, index2):
p = self.get_p()
if (self.reg_model == "normal"):
return 1
elif (self.reg_model == "binomial"):
return math.exp(eta)/float((1+math.exp(eta))**2)
elif (self.reg_model == "poisson"):
return math.exp(eta)
elif (self.reg_model == "geometric"):
return math.exp(eta)/float((1-math.exp(eta))**2)
elif (self.reg_model == "multinomial"):
denom = 1
for j in range(p):
denom += math.exp(eta[j])
val = -math.exp(eta[index1]+eta[index2])/float(denom**2)
if (index1 == index2):
val += math.exp(eta[index1])/float(denom)
return val
else:
print "No valid model has been inserted. System exiting now"
sys.exit()
# THE REMAINING RELEVANT MATRICES NEEDED TO COMPLETE THE OPTIMIZATION
# EXERCISE ARE GIVEN BELOW:
# ------generate_A(theta): Returns the (m by 1) vector whose entries
# --------------------------- are relevant values of the log-partition
# --------------------------- function. "A" is theta-dependent.
# -----------------------------------------------------------------------
# ------generate_D(theta): Returns the "D" matrix. It is theta-dependent.
# -----------------------------------------------------------------------
# ------generate_S_uk(theta, u, k): Returns the S_uk block. It is used
# --------------------------- to compute the Cost Function's Hessian.
# -----------------------------------------------------------------------
def generate_A(self, theta):
m = self.get_m()
A = np.zeros((m,1), dtype = np.float64)
for i in range (m):
A[i] = self.a_func(np.dot(self.X_train[i,::],theta.T).T)
return A
def generate_D(self, theta):
p = self.get_p()
m = self.get_m()
D = np.zeros((p,m),dtype = np.float64)
for i in range(p):
for j in range(m):
D[i,j]= self.a_first_deriv(
np.dot(self.X_train[j,::],theta.T).T, i)
return D
def generate_S_uk(self, theta, u, k):
m = self.get_m()
S_uk = np.zeros((m,m),dtype = np.float64)
for i in range(m):
S_uk[i,i] = self.a_second_deriv(
np.dot(self.X_train[i,::],theta.T).T, u, k)
return S_uk;
# THE FOLLOWING METHODS COMPUTE THE COST FUNCTION, GRADIENT, AND HESSIAN.
# ------cost_Grad_Hess(self, theta, x): Takes theta and x as input, and
# --------------------------- outputs 3 quantities:
# --------------------------- 1) Cost Function evaluated at theta and x.
# --------------------------- 2) Gradient evaluated at theta and x.
# --------------------------- (It is a p by (n+1) matrix)
# --------------------------- 3) Hessian at theta and x.
# --------------------------- (It is a p*(n+1) by p*(n+1) matrix)
# -----------------------------------------------------------------------
# ------stoch_Grad(x, i, theta): Used in stochastic gradient descent.
# --------------------------- Input i refers to the relevant training
# --------------------------- example while theta and x are as before.
# -----------------------------------------------------------------------
def cost_Grad_Hess(self, theta, x):
m = self.get_m()
n = self.get_n()
p = self.get_p()
O = np.ones((m,1), dtype = np.float64)
W = self.generate_W (x)
L = self.generate_L()
T = self.generate_T()
A = self.generate_A(theta)
D = self.generate_D(theta)
cost = float(((O.T).dot(W).dot(A) -
np.trace(self.X_train.dot(theta.T).dot(T.T).dot(W)))/float(m)
+ self.regu_lambda*np.trace(theta.dot(theta.T))/float(2))
gradient = (((D - T.T).dot(W).dot(self.X_train))/float(m) +
theta.dot(L))
hessian = np.zeros((p*(n+1), p*(n+1)), dtype = np.float64)
H_uk = np.zeros((p,p), dtype = np.float64)
for u in range(p):
for k in range(p):
S_uk = self.generate_S_uk(theta, u, k);
H_uk = ((self.X_train.T).dot(S_uk).dot(W).dot(
self.X_train))/float(m)
if (u == k):
H_uk += L
hessian[u*(n+1): (u+1)*(n+1), k*(n+1):(k+1)*(n+1)] = H_uk
return [cost, gradient, hessian]
def stoch_Grad(self, x, i, theta):
m = self.get_m()
n = self.get_n()
p = self.get_p()
T = self.generate_T()
modified_Grad = np.zeros((p,n+1), dtype = np.float64)
for j in range(p):
for k in range(n+1):
temp = (self.a_first_deriv(np.dot(
self.X_train[i,::], theta.T).T, j)*self.X_train[i,k]-
self.X_train[i,k]*T[i,j])
if (self.weight_flag == 1):
temp = temp * self.weight_bell_func(x, i)
modified_Grad[j,k] = (temp/float(m) +
self.regu_lambda*theta[j,k])
return modified_Grad
# THE FOLLOWING METHODS ARE HELPERS FOR THE VARIOUS OPTIMIZATION
# ALGORITHMS INCLUDING BATCH GRADIENT DESCENT (BGD), STOCHASTIC
# GRADIENT DESCENT (SGD) AND NEWTON RAPHSON (NR):
# ------initialize_Theta(): Sets theta to the (p by(n+1)) zero matrix.
# -----------------------------------------------------------------------
# ------vectorize(matrix): Takes a matrix, stacks all its rows in column
# --------------------------- fashion and outputs the resulting vector.
# -----------------------------------------------------------------------
# ------matricize(vector, mat_rows): Takes a vector and the number of
# --------------------------- rows for the matrix to be created. It then
# --------------------------- transforms the vector into a corresponding
# --------------------------- matrix (dimensionality-allowing).
# -----------------------------------------------------------------------
def initialize_Theta(self):
n = self.get_n()
p = self.get_p()
return np.zeros((p,n+1), dtype = np.float64)
def vectorize(self, matrix):
return matrix.flatten().T
def matricize(self, vector, mat_rows):
if ((vector.shape[0] % mat_rows) == 0):
return np.reshape(vector, (mat_rows, vector.shape[0]/mat_rows))
else:
print "Matrix dimensions not compatible with vector length."
print "System exiting now"
sys.exit()
# WE IMPLEMENT NUMERICAL OPTIMIZATION ALGORITHMS (BGD, SGD, NR):
# ------BGD(x, p, n, R, theta): Runs one iteration of BGD.
# --------------------------- R is A (p*(n+1) by p*(n+1)) diag matrix
# --------------------------- equal to the learning rate "alpha"
# --------------------------- multiplied by the identity matrix.
# --------------------------- theta is the current theta to be updated.
# --------------------------- x is the base point being fed to the
# --------------------------- predictor (it only matters in the case of
# --------------------------- weighted regression or classifiction).
# --------------------------- n is the number of input features.
# --------------------------- p is the sufficient statistic's dimension.
# --------------------------- The method returns 4 values including:
# --------------------------- 1) Updated theta after a single iteration.
# --------------------------- 2) Value of the cost function evaluated at
# --------------------------- the updated theta.
# --------------------------- 3) Value of the gradient evaluated at the
# --------------------------- updated theta.
# --------------------------- 4) Value of the hessian evaluated at the
# --------------------------- updated theta.
# -----------------------------------------------------------------------
# ------SGD(x, p, n, m, R, theta): Runs one iteration of SGD. Inputs and
# --------------------------- outputs carry the same meaning as BGD. Each
# --------------------------- iteration runs through m sub-iterations.
# -----------------------------------------------------------------------
# ------NR(x, p, n, theta): Runs one iteration of NR. The learning rate
# --------------------------- here is automatically calculated and
# --------------------------- dynamically changed for optimality. Except
# --------------------------- for R, all inputs / outputs are as before.
# -----------------------------------------------------------------------
def BGD(self, x, p, n, R, theta):
gradient = self.cost_Grad_Hess(theta, x)[1]
theta -= np.dot(R, gradient)
[cost, gradient, hessian] = self.cost_Grad_Hess(theta, x)
return theta, cost, gradient, hessian
def SGD(self, x, p, n, m, R, theta):
for i in range(m):
theta = theta - np.dot(R, self.stoch_Grad(x, i, theta))
[cost, gradient, hessian] = self.cost_Grad_Hess(theta, x)
return theta, cost, gradient, hessian
'''NOTE ON USING NR FOR MULTINOMIAL CASE:
There are convergence problems whenever Newton's method is used on a
multi-class regression problem with more than 2 classes and is hence
not recommended. A modified Hessian could be used as articulated in
http://people.stat.sc.edu/gregorkb/Tutorials/MultLogReg_Algs.pdf
'''
def NR(self, x, p, n, theta):
vectorized_theta = self.vectorize(theta)
[gradient, hessian] = self.cost_Grad_Hess(theta, x)[1:3]
vectorized_gradient = self.vectorize(gradient)
theta = self.matricize(vectorized_theta - np.dot(
np.linalg.pinv(hessian), vectorized_gradient), p)
[cost, gradient, hessian] = self.cost_Grad_Hess(theta, x)
return theta, cost, gradient, hessian
# THE 3 METHODS BELOW COMPUTE THE OPTIMAL THETA AND CONDUCT PREDICTIONS.
# ------find_Optimal_Theta(algorithm, x, iter_max, alpha = 0.01):
# --------------------------- The algorithm is a string indicating "BGD",
# --------------------------- "SGD", or "NR".
# --------------------------- x is the input on which prediction will be
# --------------------------- conducted. It is encoded as a column
# --------------------------- vector. Note that theta's dependence on
# --------------------------- x is only applicable in the case of a
# --------------------------- weighted learning.
# --------------------------- iter_max is the max number of iterations
# --------------------------- for the algorithm.
# --------------------------- alpha is the learning rate (relevant to
# --------------------------- BGD and SGD only).
# --------------------------- The method returns 2 values:
# --------------------------- 1) The updated theta returned by the
# --------------------------- algorithm after iter_max iterations.
# --------------------------- 2) A list containing the value of
# --------------------------- the cost function after each
# --------------------------- iteration (useful in case we want
# --------------------------- to plot the cost value vs. iterations
# --------------------------- and check for convergence).
# -----------------------------------------------------------------------
# ------predict(x, theta): Applies the corresponding predictor based
# --------------------------- on the chosen probabilistic model x is the
# --------------------------- input point represented as a column vector.
# -----------------------------------------------------------------------
# ------fit(algorithm, X_predict, iter_max, alpha = 0.01):
# --------------------------- The algorithm is a string indicating "BGD",
# --------------------------- "SGD", or "NR".
# --------------------------- X_predicted is the input matrix (can be a
# --------------------------- vector in case of single input or a
# --------------------------- matrix in case prediction is conducted
# --------------------------- on many input vectors. X_predicted is
# --------------------------- augmented with the all-1 column and
# --------------------------- has the same structure as X_train.
# --------------------------- The method returns 3 values including:
# --------------------------- 1) theta_optimal (it is a single value in
# --------------------------- case of non-weighted learning, or a
# --------------------------- list of values corresponding to each
# --------------------------- input in case of weighted learning.
# --------------------------- 2) A list containing the value of the cost
# --------------------------- function after each iteration until
# --------------------------- theta_optimal is calculated (note that
# --------------------------- in case of non-weighted learning, we
# --------------------------- get a single list of cost values. But
# --------------------------- if weighted learning is applied, each
# --------------------------- input will have a different
# --------------------------- theta_optimal and hence get an
# --------------------------- associated list of cost values).
# --------------------------- 3) An array of the predicted values
# --------------------------- corresponding to each input.
# -----------------------------------------------------------------------
def find_Optimal_Theta(self, algorithm, x, iter_max, alpha = 0.01):
p = self.get_p()
n = self.get_n()
m = self.get_m()
R = np.eye(p,p, dtype = np.float64) * alpha;
theta = self.initialize_Theta()
cost = [0] * iter_max
iter_count = 0
if (algorithm == "BGD"):
while(iter_count < iter_max):
theta, cost[iter_count] = self.BGD(x, p, n, R,
theta)[0:2]
iter_count += 1
elif (algorithm == "SGD"):
while(iter_count < iter_max):
theta, cost[iter_count] = self.SGD(x, p, n, m, R,
theta)[0:2]
iter_count += 1
elif (algorithm == "NR"):
while(iter_count < iter_max):
theta, cost[iter_count] = self.NR(x, p, n, theta)[0:2]
iter_count += 1
else:
print "No valid model has been inserted. System exiting now"
sys.exit()
return theta, cost
def predict(self, x, theta):
p = self.get_p()
predicted = np.zeros((p,1),dtype = np.float64)
for i in range(p):
predicted[i,0] = self.a_first_deriv(np.dot(theta,x), i)
if (self.reg_model in ["normal", "poisson", "geometric"]):
return predicted[0,0];
elif (self.reg_model == "binomial"):
return predicted[0,0] > 0.5
elif (self.reg_model == "multinomial"):
max_val = predicted.max();
sum_val = predicted.sum();
max_index = np.argmax(predicted)
if (max_val < (1-sum_val)):
return p
else:
return max_index
def fit(self,algorithm, X_predict, iter_max, alpha = 0.01):
l = X_predict.shape[0]
Y_predict = np.zeros((l, 1), dtype = np.float64)
if (self.weight_flag == 0):
theta_optimal, cost = self.find_Optimal_Theta(
algorithm, X_predict.T[::,0], iter_max, alpha)
for element in range(l):
Y_predict[element,0] = self.predict(
X_predict.T[::,element], theta_optimal)
return theta_optimal, cost, Y_predict
elif (self.weight_flag == 1):
theta_optimal = []
cost = []
for element in range(l):
theta_new, cost_new = self.find_Optimal_Theta(
algorithm, X_predict.T[::,element], iter_max, alpha)
theta_optimal.append(theta_new);
cost.append(cost_new)
Y_predict[element,0] = self.predict(
X_predict.T[::,element], theta_optimal[element])
return theta_optimal, cost, Y_predict
9. References
[1] Stephen Boyd and Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004.
[2] Karl Gregory. Multinomial logistic regression algorithms, 2018.
[3] Bent Jorgensen. Exponential dispersion models. Journal of the Royal Statistical Society, 49(2):127 162, 1987.
Tags: GLM, machine learning, ML, multivariate gaussian, supervised learning

No comments
Comments feed for this article
Trackback link: https://delfr.com/generalized-linear-model/trackback/