1. Introduction
Pedersen Commitments are at the heart of how Monero conceals transaction amounts. The notion of a confidential transaction as enabled by Pedersen Commitments were outlined and defined by Gregory Maxwell in [1]. In what follows we first introduce the notion of a group homomorphism (of which the Pedersen Commitment map is a particular instance), we then define the Pedersen Commitment map, and finally present the mechanisms of a confidential transaction enabled by a such a map.
2. Group homomorphism
Let ![]() and
and ![]() be 2 groups with respective group operations
be 2 groups with respective group operations ![]() and
and ![]() . A function
. A function ![]() is called a group homomorphism if and only if
is called a group homomorphism if and only if
![]()
In other terms, operating on 2 elements in ![]() and then applying
and then applying ![]() is equivalent to applying
is equivalent to applying ![]() on each element separately and then operating on the 2 outputs in
on each element separately and then operating on the 2 outputs in ![]() .
.
We now introduce a specific instance of a group homomorphism that we will invoke when concealing transaction amounts with Monero as part of the confidential transaction construct. In particular, we conduct arithmetic in the subgroup ![]() of the elliptic curve group
of the elliptic curve group ![]() introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic)
introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic)
Let ![]() , and let
, and let ![]() where
where ![]() denotes element-wise addition in modulo
denotes element-wise addition in modulo ![]() arithmetic over
arithmetic over ![]()
It is a known result in group theory that if ![]() is a generator of a cyclic group
is a generator of a cyclic group ![]() of order
of order ![]() , then there are
, then there are ![]() elements of the group that have order
elements of the group that have order ![]() (
(![]() is the euler function introduced in part 1). In our case, the generator
is the euler function introduced in part 1). In our case, the generator ![]() of
of ![]() has prime order
has prime order ![]() . Moreover
. Moreover ![]() (since
(since ![]() is prime). Hence we can find
is prime). Hence we can find ![]() other generators of
other generators of ![]() . Let
. Let ![]() be another generator such that the DL (discrete logarithm) of
be another generator such that the DL (discrete logarithm) of ![]() with respect to
with respect to ![]() is unknown. We define the Pedersen Commitment map (which we will later use to build a confidential transaction) as follows:
is unknown. We define the Pedersen Commitment map (which we will later use to build a confidential transaction) as follows:
![]()
![]()
We claim that the map ![]() is additively homomorphic. To see why, let
is additively homomorphic. To see why, let ![]() We then have:
We then have:
![]()
![]()
(where ![]() denotes
denotes ![]() over
over ![]() )
)
![]()
hence ![]() is homomorphic.
is homomorphic.
We call ![]() a commitment.
a commitment. ![]() denotes the amount we commit to, while
denotes the amount we commit to, while ![]() is referred to as the blinding factor. Note that
is referred to as the blinding factor. Note that ![]() , there always exists a blinding factor
, there always exists a blinding factor ![]() such that
such that ![]() Indeed, given
Indeed, given ![]() and
and ![]() , an adequate
, an adequate ![]() must satisfy
must satisfy ![]() (by definition of the map
(by definition of the map ![]() ). This is equivalent to finding
). This is equivalent to finding ![]() such that
such that ![]() denotes the additive inverse of
denotes the additive inverse of ![]() over the group
over the group ![]() Since
Since ![]() and since
and since ![]() is a generator of
is a generator of ![]() , we can be certain of the existence of such an
, we can be certain of the existence of such an ![]()
Note that this does not mean that we can find the value of ![]() since this would require finding the DL of
since this would require finding the DL of ![]() in base
in base ![]() . However, it means that for a given amount
. However, it means that for a given amount ![]() , one could achieve any commitment value
, one could achieve any commitment value ![]() by appropriately choosing
by appropriately choosing ![]() . A consequence of this is if we are given
. A consequence of this is if we are given ![]() and we randomly choose
and we randomly choose ![]() , then
, then ![]() would look random over
would look random over ![]() So given a transaction amount
So given a transaction amount ![]() , one can randomly generate a blinding factor
, one can randomly generate a blinding factor ![]() and calculate
and calculate ![]() We now introduce the notion of a confidential transaction.
We now introduce the notion of a confidential transaction.
3. Confidential transaction
In Bitcoin, transaction amounts are openly published to allow the network to verify that no value was created out of thin air or destroyed. The Bitcoin network checks that for each transaction, the total input amount of relevant UTXOs (denoted by ![]() ) is equal to that of the output UTXOs (denoted by
) is equal to that of the output UTXOs (denoted by ![]() ). It must be that
). It must be that
![]()
The question that a confidential transaction scheme must answer is whether the above equation can be verified without accessing the exact transaction values ![]() and
and ![]() . We now describe a method that solves the question by using the homomorphic Pedersen Commitment previously introduced. Without loss of generality:
. We now describe a method that solves the question by using the homomorphic Pedersen Commitment previously introduced. Without loss of generality:
 , let
, let 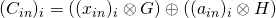 be the Pedersen Commitment associated with amount
be the Pedersen Commitment associated with amount 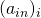 with blinding factor
with blinding factor  randomly chosen in
randomly chosen in 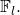
- Let
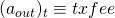 be the miner’s transaction fee and let
be the miner’s transaction fee and let 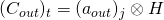 be the Pedersen Commitment associated with txfee. The blinding factor
be the Pedersen Commitment associated with txfee. The blinding factor 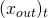 is deliberatly chosen to be 0 (i.e., the identity element of
is deliberatly chosen to be 0 (i.e., the identity element of 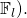
 , let
, let  be the Pedersen Commitment associated with amount
be the Pedersen Commitment associated with amount  with blinding factor
with blinding factor 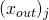 randomly chosen in
randomly chosen in  . We additionaly require that
. We additionaly require that 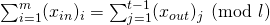 (the rationale will become clear in the next paragraph).
(the rationale will become clear in the next paragraph).
Suppose that:
![]()
This is equivalent to:
![]()
(by definition of txfee and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
(by invoking the additive homomorphic property of the Pedersen Commitment map)
![]()
![]()
![]()
![]()
where ![]() and
and ![]() are addition and subtraction in modulo
are addition and subtraction in modulo ![]() arithmetic over
arithmetic over ![]() By design, the left hand side is 0 (because
By design, the left hand side is 0 (because ![]() ). We can thus conclude that if
). We can thus conclude that if ![]() , then:
, then:
![]()
![]()
By ensuring that
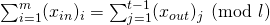 , and
, and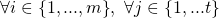 the amounts
the amounts 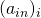 and
and  remain confined to a pre-defined range
remain confined to a pre-defined range ![Rendered by QuickLaTeX.com [0, 2^r] \subset \mathbb{F}_l.](https://delfr.com/wp-content/ql-cache/quicklatex.com-859780b007868ccad80a5e14b5a2a663_l3.png)
 is chosen in such a way that
is chosen in such a way that 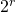 is significantly smaller than
is significantly smaller than  . More specifically, suppose
. More specifically, suppose  and
and 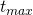 respectively denote the maximum number of inputs and outputs that can be used in any given transaction. By letting
respectively denote the maximum number of inputs and outputs that can be used in any given transaction. By letting 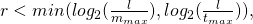 we are guaranteed that:
we are guaranteed that:
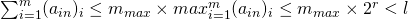
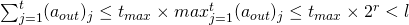
we get the following equivalence:
![]()
![]()
It is important to note that the amounts balance out in actuality and not in the more relaxed ![]() sense. This is because of the constraint we imposed on all transaction amounts to be confined to the
sense. This is because of the constraint we imposed on all transaction amounts to be confined to the ![]() range. If this constraint was no imposed, one would be able to create or destroy Monero currency while still maintaining a balanced equation. To see this, suppose transaction amounts can take on any value in
range. If this constraint was no imposed, one would be able to create or destroy Monero currency while still maintaining a balanced equation. To see this, suppose transaction amounts can take on any value in ![]() instead of being restricted to
instead of being restricted to ![]() Let
Let ![]() with
with ![]() Also let
Also let ![]() with
with ![]()
Clearly, ![]()
However, ![]()
If this transaction gets approved by the network, we would have effectively destroyed ![]() units of currency. Conversely, exchanging the input and output values would allow the creation of
units of currency. Conversely, exchanging the input and output values would allow the creation of ![]() units of currency out of thin air. This example demonstrates the importance of having a balanced equation independent of modulo
units of currency out of thin air. This example demonstrates the importance of having a balanced equation independent of modulo ![]() arithmetic. By confining all transaction amounts to the
arithmetic. By confining all transaction amounts to the ![]() range, we ensure that this is the case. To prove that a transaction amount lies in a certain range, Monero makes use of the Borromean signature construct. We are not covering its mechanics in this work but the interested reader can consult [2].
range, we ensure that this is the case. To prove that a transaction amount lies in a certain range, Monero makes use of the Borromean signature construct. We are not covering its mechanics in this work but the interested reader can consult [2].
The result above allows one to safely replace the transaction amounts by their respective Pedersen Commitments (i.e., hide the transaction amounts) while still ensuring proper accounting.
References
[1] Greg Maxwell. Confidential transactions, 2015.
[2] G. Maxwell and A. Poelstra. Borromean ring signatures. 2015.
Tags: anonymity, confidential transaction, Monero, Pedersen commitment

No comments
Comments feed for this article
Trackback link: https://delfr.com/confidential-transaction-moneros-part-8/trackback/