1. Introduction
For a given ring size ![]() , Cryptonote’s original scheme (as introduced in part 5), generates signatures of the form
, Cryptonote’s original scheme (as introduced in part 5), generates signatures of the form ![]() consisting of
consisting of ![]() arguments. It turns out that a more efficient scheme initially introduce in [3] and later adapted by Adam Back in [1] can achieve the same security properties as Cryptonote’s with
arguments. It turns out that a more efficient scheme initially introduce in [3] and later adapted by Adam Back in [1] can achieve the same security properties as Cryptonote’s with ![]() arguments instead (a reduction factor that tends to 2 as
arguments instead (a reduction factor that tends to 2 as ![]() tends to
tends to ![]() ). The scheme introduced in [3] is known as Linkable Spontaneous Anonymous Group signature or LSAG signature scheme for short. In part 7 of this series, we will see how [4] generalizes the LSAG construct to build the foundation of Monero’s current ringCT signature scheme.
). The scheme introduced in [3] is known as Linkable Spontaneous Anonymous Group signature or LSAG signature scheme for short. In part 7 of this series, we will see how [4] generalizes the LSAG construct to build the foundation of Monero’s current ringCT signature scheme.
2. The LSAG scheme
The LSAG signature introduced in [3] is built on a group ![]() of prime order
of prime order ![]() and generator
and generator ![]() . Moreover, it uses 2 statistically independent ROs:
. Moreover, it uses 2 statistically independent ROs:
In what follows we introduce a slightly modified LSAG scheme that will allow an easier comparison to Cryptonote’s original scheme. We carry forward all the notation used in the Cryptonote scheme to the current LSAG definition. In particular, we let ![]() be a large finite group generated by the same elliptic curve introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic). We also consider the same base point
be a large finite group generated by the same elliptic curve introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic). We also consider the same base point ![]() . Recall that the base point is chosen in such a way to ensure that it has a large prime order
. Recall that the base point is chosen in such a way to ensure that it has a large prime order ![]() All arithmetic is done in the subgroup
All arithmetic is done in the subgroup ![]() of the elliptic curve group
of the elliptic curve group ![]() As a matter of convention, we write
As a matter of convention, we write ![]()
With a slight divergence from [3], we first introduce a hash function ![]() before we define
before we define ![]() . The reason will become clearer in section 4 when we build the signing simulator to prove LSAG’s resilience against EFACM.
. The reason will become clearer in section 4 when we build the signing simulator to prove LSAG’s resilience against EFACM.
![]() takes an element
takes an element ![]() and outputs a tuple
and outputs a tuple ![]() . Here
. Here ![]() is a random element chosen according to a uniform distribution over
is a random element chosen according to a uniform distribution over ![]() . We then let
. We then let ![]() . So
. So ![]() , takes an element
, takes an element ![]() and returns an element
and returns an element ![]() where
where ![]() is randomly chosen in
is randomly chosen in ![]()
Note that [3] defines ![]() as a map from
as a map from ![]() to
to ![]() . Here we restricted the domain and the range to
. Here we restricted the domain and the range to ![]() instead. This is because in this version of LSAG,
instead. This is because in this version of LSAG, ![]() is strictly applied to public keys as opposed to any element of
is strictly applied to public keys as opposed to any element of ![]() . Public keys are elements of
. Public keys are elements of ![]() that are scalar multiples of the base point
that are scalar multiples of the base point ![]() . Moreover, the scalar is never equal to order(
. Moreover, the scalar is never equal to order(![]() )
) ![]() (we impose this constraint when we introduce the key generation algorithm
(we impose this constraint when we introduce the key generation algorithm ![]() ). We are then justified in restricting the domain to
). We are then justified in restricting the domain to ![]() . The range is arbitrarily defined to be
. The range is arbitrarily defined to be ![]() , which is permissible since it preserves the injective nature of the map.
, which is permissible since it preserves the injective nature of the map.
The LSAG scheme is defined by a set of 4 algorithms:
- The key generation algorithm
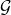 . On input
. On input 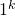 (
(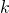 is the security parameter that by design we request to satisfy
is the security parameter that by design we request to satisfy 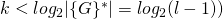 , it produces a pair
, it produces a pair 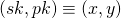 of matching secret and public keys.
of matching secret and public keys.  is randomly chosen in
is randomly chosen in 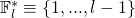 , and
, and  is calculated as
is calculated as 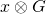 . (Note that
. (Note that 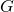 and
and  are both elements of
are both elements of 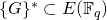 while
while 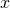 is an element of
is an element of 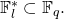 In addition to the
In addition to the 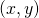 key pair,
key pair, 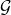 computes
computes 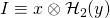 .
.  is known as the key image (or tag). It is signer-specific since it depends only on the signer’s private and public keys. It allows the ring linkability algorithm
is known as the key image (or tag). It is signer-specific since it depends only on the signer’s private and public keys. It allows the ring linkability algorithm  to test for independence between different signatures.
to test for independence between different signatures.  is modeled as a PPT Turing machine. We observe that in [3], the key-image or tag is computed as part of the ring signing algorithm
is modeled as a PPT Turing machine. We observe that in [3], the key-image or tag is computed as part of the ring signing algorithm 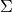 as opposed to
as opposed to 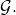 We include it in
We include it in 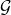 to ensure consistency with Cryptonote’s original construct.
to ensure consistency with Cryptonote’s original construct. - The ring signing algorithm
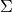 . Suppose a user
. Suppose a user 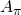 decides to sign a message
decides to sign a message 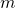 on behalf of the ring of users
on behalf of the ring of users 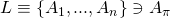 .
. 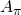 has a key pair given by
has a key pair given by 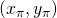 and a key-image (or tag) given by
and a key-image (or tag) given by 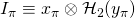 .
. 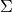 does the following:
does the following:
- Choose random
 . Assign:
. Assign:
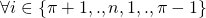 , pick random
, pick random 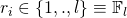 . Assign:
. Assign:
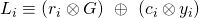
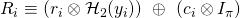
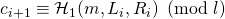 , where
, where 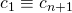
- Set
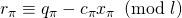 . Here
. Here 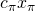 denotes regular scalar multiplication in modulo
denotes regular scalar multiplication in modulo 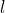 arithmetic.
arithmetic.
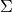 outputs a signature
outputs a signature 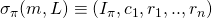 .
. 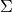 is a PPT algorithm.
is a PPT algorithm. - Choose random
- The ring verification algorithm
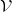 . Given a ring signature
. Given a ring signature 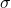 , a message
, a message 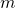 , and the set
, and the set 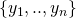 of public keys of the ring members:
of public keys of the ring members:
- (Verification equations #1 to
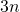 ): let
): let 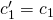 .
. 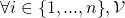 assigns
assigns
- (Verification equation
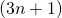 ):
): 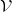 checks whether
checks whether
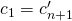 , where
, where 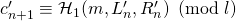
If equality holds, the signature is valid and
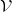 outputs True. Otherwise, it outputs False.
outputs True. Otherwise, it outputs False. 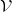 is a deterministic algorithm.
is a deterministic algorithm.
- (Verification equations #1 to
- The ring linkability algorithm
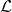 . It takes a
. It takes a 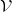 -verified valid signature
-verified valid signature 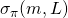 . It checks if the key-image
. It checks if the key-image 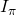 was used in the past by comparing it to previous key-images stored in a set
was used in the past by comparing it to previous key-images stored in a set 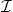 . If a match is found, then with overwhelming probability the 2 signatures were produced by the same key pair (as will be justified when we prove the exculpability of LSAG in section 5 below), and
. If a match is found, then with overwhelming probability the 2 signatures were produced by the same key pair (as will be justified when we prove the exculpability of LSAG in section 5 below), and 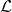 outputs Linked. Otherwise, its key-image is added to
outputs Linked. Otherwise, its key-image is added to 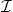 and
and 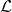 outputs Independent.
outputs Independent.
3. Security analysis – Correctness
Let ![]() be an LSAG
be an LSAG ![]() -generated signature. Without loss of generality, assume
-generated signature. Without loss of generality, assume ![]() . Then
. Then ![]() , we have the following implication:
, we have the following implication:
If ![]() , then:
, then:
Recall that ![]() (by design of
(by design of ![]() ) and so
) and so ![]() and
and ![]() . We therefore conclude by induction on
. We therefore conclude by induction on ![]() that
that ![]() ,
, ![]() . In particular,
. In particular, ![]() . This implies:
. This implies:
We can then invoke a similar induction argument on ![]() as the one stated earlier, but this time for
as the one stated earlier, but this time for ![]() . We therefore conclude that:
. We therefore conclude that:
![]()
(by design of ![]() )
)
![]()
(by induction proof showing that ![]() and
and ![]() )
)
Subsequently, any ![]() -generated LSAG signature will satisfy
-generated LSAG signature will satisfy ![]() ‘s verification test.
‘s verification test.
4. Security analysis – Unforgeability vis-a-vis EFACM
For unforgeability proofs, we follow the 5-step approach outlined earlier in part 1. (Recall that for ring signatures, we prove resilience against EFACM with respect to a fixed ring attack as described in part 3).
Step 1: To prove that the LSAG scheme is secure against EFACM in the RO model, we proceed by contradiction and assume that there exists a PPT adversary ![]() such that:
such that:
![]()
for ![]() non-negligible in
non-negligible in ![]()
Step 2: Next, we build a simulator ![]() such that it:
such that it:
- Does not have access to the private key of any signer.
- Has the same range as the original signing algorithm
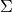 (i.e., they output signatures taken from the same pool of potential signatures over all possible choices of RO functions and random tapes
(i.e., they output signatures taken from the same pool of potential signatures over all possible choices of RO functions and random tapes 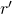 and
and  ).
). - Has indistinguishable probability distribution from that of
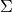 over this range.
over this range.

The reason we introduced ![]() as opposed to introducing only
as opposed to introducing only ![]() is that the simulator makes use of the random element
is that the simulator makes use of the random element ![]() in order to set
in order to set ![]() to the desired value. In other words, the simulator needs to have access to the random element
to the desired value. In other words, the simulator needs to have access to the random element ![]() that is used in the calculation of
that is used in the calculation of ![]() in order to ensure that
in order to ensure that ![]() equates to
equates to ![]() .
.
By construction, the output of ![]() will satisfy the verification equation. Moreover, it does its own random assignments to what otherwise would be calls to RO
will satisfy the verification equation. Moreover, it does its own random assignments to what otherwise would be calls to RO ![]() (i.e.,
(i.e., ![]() bypasses RO
bypasses RO ![]() ). Next, note the following:
). Next, note the following:
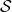 does not use any private key.
does not use any private key.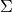 and
and 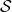 both have a range
both have a range 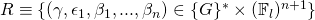 such that
such that 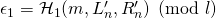 and where
and where 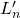 and
and 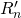 are calculated as follows:
are calculated as follows:
- Let
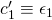
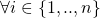 , compute:
, compute:
- Let
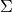 and
and 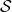 have the same probability distribution over
have the same probability distribution over 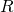 . Indeed,
. Indeed, 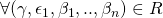 , we have:
, we have:
- For

![Rendered by QuickLaTeX.com P[(I_{\pi},c_1,r_1,..,r_n) = (\gamma, \epsilon_1,\beta_1,...,\beta_n)] =](https://delfr.com/wp-content/ql-cache/quicklatex.com-0c379913523c5c53c5affcbd093d521e_l3.png)
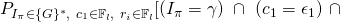
![Rendered by QuickLaTeX.com (r_i = \beta_i,\ \forall i \in \{{1,...,n\}})]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e9cbd45996da8359926c2d541c909ac1_l3.png)
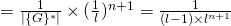
The first factor is the probability of choosing the exact
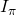 value in the set
value in the set 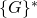 that is equal to
that is equal to 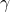 . The second factor is the probability of choosing the exact
. The second factor is the probability of choosing the exact 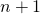 values given by
values given by 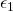 and the
and the 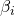 ‘s
‘s 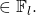
- For
 :
:
![Rendered by QuickLaTeX.com P[(I_{\pi}^{\sim}, c^{\sim}_1,r^{\sim}_1,..,r^{\sim}_n) = (\gamma, \epsilon_1, \beta_1,...,\beta_n)] =](https://delfr.com/wp-content/ql-cache/quicklatex.com-cb566a3b8f02b7d0ce3645c4edf6c27c_l3.png)
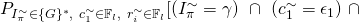
![Rendered by QuickLaTeX.com (r_i^{\sim} = \beta_i,\ \forall i \in \{{1,...,n\}})]](https://delfr.com/wp-content/ql-cache/quicklatex.com-903194ed727e4984ea64db3a81d94416_l3.png)
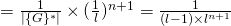
Note that the range of
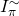 is equal to
is equal to 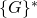 by construction of
by construction of 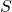 . And so the first factor is the probability of choosing the exact
. And so the first factor is the probability of choosing the exact 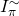 value in the set
value in the set 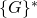 that is equal to
that is equal to 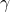 . The second factor is the probability of choosing the exact
. The second factor is the probability of choosing the exact 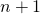 values given by
values given by 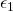 and the
and the 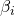 ‘s
‘s 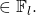
- For
With ![]() adequately built, we conclude that (refer to section 6 of part 1 for a justification):
adequately built, we conclude that (refer to section 6 of part 1 for a justification):
![]() , for
, for ![]() non-negligible in
non-negligible in ![]()
Step 3: We now show that the probability of faulty collisions is negligible (refer to section 6 of part 1 for an overview). The 2 tyes of collisions are:
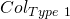 : there exists
: there exists 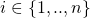 such that a tuple
such that a tuple 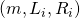 that
that 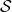 encounters — recall that
encounters — recall that 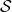 makes its own random assignment to
makes its own random assignment to 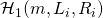 and bypasses RO
and bypasses RO 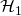 — also appears in the list of queries that
— also appears in the list of queries that 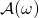 sends to RO
sends to RO 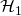 . A conflict in the 2 values will happen with overwhelming probability and the execution will halt.
. A conflict in the 2 values will happen with overwhelming probability and the execution will halt.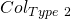 : there exists
: there exists 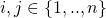 such that a tuple
such that a tuple 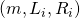 that
that 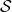 encounters — recall that
encounters — recall that 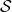 makes its own random assignment to
makes its own random assignment to 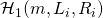 — is the same as another tuple
— is the same as another tuple 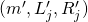 that
that 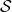 encountered earlier — here too,
encountered earlier — here too, 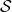 would have made its random assignment to
would have made its random assignment to 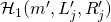 . Since the tuples are identical (i.e.,
. Since the tuples are identical (i.e., 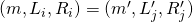 ), the assignments must match (i.e.,
), the assignments must match (i.e., 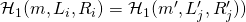 . However, the likelihood that the 2 are equal is negligible. Hence they will be different with overwhelming probability and the execution will halt.
. However, the likelihood that the 2 are equal is negligible. Hence they will be different with overwhelming probability and the execution will halt.
The aforementioned collisions must be avoided. In order to do so, we first calculate the probability of their occurence. We assume that during an EFACM attack, ![]() can make a maximum of
can make a maximum of ![]() queries to RO
queries to RO ![]() , a maximum of
, a maximum of ![]() queries to RO
queries to RO ![]() , and a maximum of
, and a maximum of ![]() queries to
queries to ![]() .
. ![]() ,
, ![]() , and
, and ![]() are all assumed to be polynomial in the security parameter
are all assumed to be polynomial in the security parameter ![]() , since the adversary is modeled as a PPT Turing machine.
, since the adversary is modeled as a PPT Turing machine.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Recalling that ![]() and
and ![]() are polynomial in
are polynomial in ![]() , we conclude that
, we conclude that ![]() is negligible in
is negligible in ![]()
Next, we compute ![]()
![]()
![]()
![]()
![]()
![]()
(since ![]() by design).
by design).
Recalling that ![]() is polynomial in
is polynomial in ![]() , we conclude that
, we conclude that ![]() is negligible in
is negligible in ![]()
Putting it altogether, we find that the below quantity is negligible in ![]()
![]()
![]()
This allows us to conclude that the below quantity is non-negligible in ![]() (refer to section 6 of part 1 for a justification):
(refer to section 6 of part 1 for a justification):
![]()
Step 4: In this step, our objective is to show that if ![]() is a successful tuple that generated a first EFACM forgery, then the following quantity is non-negligible in
is a successful tuple that generated a first EFACM forgery, then the following quantity is non-negligible in ![]()
![]()
![]()
![]()
Here ![]() is an appropriate index that we will define in the proof. Moreover,
is an appropriate index that we will define in the proof. Moreover, ![]() and
and ![]() for all
for all ![]() . (
. (![]() and
and ![]() denote respectively the
denote respectively the ![]() query to
query to ![]() and to
and to ![]() ).
).
Let’s take a closer look at
![]()
Any successful forgery ![]() must pass the verification equation
must pass the verification equation ![]() where we let
where we let ![]() , and
, and ![]() :
:
We distinguish between 3 scenarios (without loss of generality, we assume that all ![]() -queries sent to RO
-queries sent to RO ![]() are distinct from each-other. Similarly, all
are distinct from each-other. Similarly, all ![]() -queries sent to RO
-queries sent to RO ![]() are distinct from each-other. This is because we can assume that
are distinct from each-other. This is because we can assume that ![]() keeps a local copy of previous query results and avoid redundant calls):
keeps a local copy of previous query results and avoid redundant calls):
- Scenario 1:
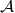 was successful in its forgery, and
was successful in its forgery, and
- No collisions occured, and
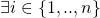 such that it never queried RO
such that it never queried RO 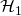 on input
on input 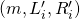 .
.
- Scenario 2:
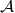 was successful in its forgery, and
was successful in its forgery, and
- No collisions occured, and
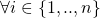 it queried RO
it queried RO 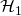 on input
on input 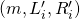 during execution, and
during execution, and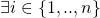 such that it queried RO
such that it queried RO 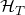 on input
on input 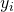 after it had queried RO
after it had queried RO 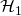 on input
on input 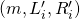 .
.
- Scenario 3:
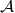 was successful in its forgery, and
was successful in its forgery, and
- No collisions occured, and
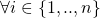 it queried RO
it queried RO 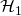 on input
on input 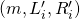 during execution, and
during execution, and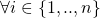 , it queried RO
, it queried RO 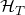 on input
on input 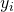 before it queried RO
before it queried RO 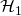 on input
on input 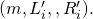
The probability of scenario 1 is upper-bounded by the probability that ![]() picks
picks ![]() such that it matches the value of
such that it matches the value of ![]() . If the 2 values don’t match, then
. If the 2 values don’t match, then ![]() will be different than
will be different than ![]() (by the verification algorithm
(by the verification algorithm ![]() ). It is upper-bounded because at the very least, this constraint must be observed to pass the verification test. Here,
). It is upper-bounded because at the very least, this constraint must be observed to pass the verification test. Here, ![]() is the value that RO
is the value that RO ![]() returns to
returns to ![]() (the verification algorithm) when verifying the validity of the forged signature. And since
(the verification algorithm) when verifying the validity of the forged signature. And since ![]() can be any value in the range of
can be any value in the range of ![]() (which was defined to be
(which was defined to be ![]() ) we get:
) we get:
![]()
which is negligible in ![]()
In scenario 2, let ![]() be an index such that
be an index such that ![]() queried RO
queried RO ![]() on input
on input ![]() after it had queried RO
after it had queried RO ![]() on input
on input ![]() . Note that during the verification process,
. Note that during the verification process, ![]() will calculate
will calculate ![]() and hence will make a call to
and hence will make a call to ![]() on input
on input ![]() (remember that
(remember that ![]() is derived from
is derived from ![]() ). The probability that the resulting
). The probability that the resulting ![]() matches the
matches the ![]() argument previously fed to
argument previously fed to ![]() is upper-bounded by
is upper-bounded by ![]() (since the range of
(since the range of ![]() ). Moreover,
). Moreover, ![]() can be any index in
can be any index in ![]() . We get:
. We get:
![]() , which is negligible in
, which is negligible in ![]()
So we assume that a successful forgery will likely be of the Scenario 3 type.
![]()
![]()
![]() , which is non-negligible in
, which is non-negligible in ![]()
Note that ![]() can send queries to RO
can send queries to RO ![]() and RO
and RO ![]() in any order it chooses to. This gives 2 different ways of referencing the index of a particular query sent to RO
in any order it chooses to. This gives 2 different ways of referencing the index of a particular query sent to RO ![]() . One way is to count the index as it appeared in the sequence of cumulative queries sent to both
. One way is to count the index as it appeared in the sequence of cumulative queries sent to both ![]() and
and ![]() . In this case, indices take on values in
. In this case, indices take on values in ![]() . The other way, is to do the counting with respect to
. The other way, is to do the counting with respect to ![]() queries only causing indices to take on values in
queries only causing indices to take on values in ![]() . If
. If ![]() is the index counted in the cumulative numbering system (i.e., the former system), we let
is the index counted in the cumulative numbering system (i.e., the former system), we let ![]() be the equivalent index in the latter system. Clearly,
be the equivalent index in the latter system. Clearly, ![]()
By definition of scenario 3, we know for a fact that ![]() , there exists an integer
, there exists an integer ![]() such that
such that ![]() is the index of the query
is the index of the query ![]() . We define
. We define ![]() to be the vector of indices
to be the vector of indices ![]() corresponding to the queries
corresponding to the queries ![]() that
that ![]() sends to RO
sends to RO ![]() during execution. Here, indexing is with respect to the cumulative numbering system. We let
during execution. Here, indexing is with respect to the cumulative numbering system. We let ![]() if query
if query ![]() was never asked by
was never asked by ![]() . We also define the following condition:
. We also define the following condition:
![]()
![]()
This definition allows us to build the following sets:
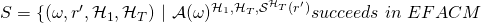
![Rendered by QuickLaTeX.com \cap\ \overline{Col}\ \cap\ E\ \cap\ max_{i=1}^n[Ind(\omega, r', \mathcal{H}_1, \mathcal{H}_T) \neq \infty] \}}](https://delfr.com/wp-content/ql-cache/quicklatex.com-c961dbce3c5df8a77c5abf46f6cac58a_l3.png)
In other terms,
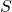 is the set of tuples
is the set of tuples 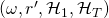 that yield a successful EFACM forgery when no collisions occur, and when
that yield a successful EFACM forgery when no collisions occur, and when 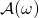 queried RO
queried RO 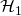 on input
on input 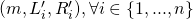 at some point during its execution such that condition
at some point during its execution such that condition 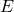 is met. This is none other than scenario 3.
is met. This is none other than scenario 3.-
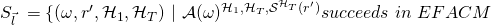
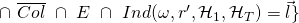
where
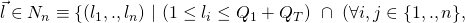
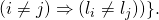
We let
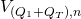 denote that the cardinality of
denote that the cardinality of 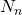 . We have
. We have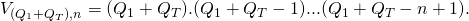
We can see that
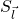 represents the set of tuples
represents the set of tuples 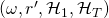 that yield a successful EFACM forgery when no collisions occur, and when
that yield a successful EFACM forgery when no collisions occur, and when 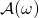 queried RO
queried RO 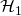 on all
on all 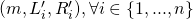 such that the index of the input query
such that the index of the input query 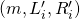 is equal to
is equal to 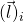 (i.e., the
(i.e., the 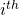 component of
component of 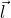 ), and such that condition
), and such that condition 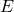 is met.
is met.
Recall that
![]()
(non-negligible in ![]() )
)
Clearly, ![]() partitions
partitions ![]() . So
. So
![]()
This implies that
![]()
![]()
If this were not the case, then one would get the following contradiction:
![]()
![]()
So we introduce the set ![]() consisting of all vectors
consisting of all vectors ![]() that meet the
that meet the ![]() threshold, i.e.
threshold, i.e.
![]()
We claim that
![]()
Proof: By definition of the sets ![]() , we have:
, we have:
![]()
![]()
![]()
![]()
The next step is to apply the splitting lemma to each ![]() . First note that:
. First note that:
![]()
![]()
![]()
![]()
![]()
Let ![]() . Referring to the notation used in the splitting lemma (section 7 of part 1), we let:
. Referring to the notation used in the splitting lemma (section 7 of part 1), we let:
![]() is defined as the space of tuples of:
is defined as the space of tuples of:
- All random tapes
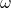
- All random tapes
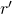
- All possibe RO
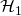 answers to the first (
answers to the first (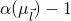 ) queries sent by
) queries sent by 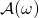 (note the usage of
(note the usage of 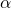 -indexing since indexing is done with respect to RO
-indexing since indexing is done with respect to RO 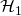 queries only)
queries only) - All RO
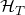 (this means all possible RO
(this means all possible RO 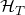 answers to the
answers to the 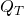 queries sent by
queries sent by 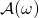 ).
).
![]() is defined as the space of all possible RO
is defined as the space of all possible RO ![]() answers to the last
answers to the last ![]() queries sent by
queries sent by ![]() . (Recall that
. (Recall that ![]() where
where ![]() is the
is the ![]() query sent to RO
query sent to RO ![]() ).
).
The splitting lemma guarantees the existence of a subset ![]() of tuples
of tuples ![]() such that:
such that:
![Rendered by QuickLaTeX.com P_{\omega,r',\mathcal{H}_1, \mathcal{H}_T}[(\omega, r', \mathcal{H}_1, \mathcal{H}_T) \in \Omega_{\vec{l}}] \geq \frac{\nu(k)}{4V{(Q_1 + Q_T),n}}](https://delfr.com/wp-content/ql-cache/quicklatex.com-ca660fd86db7ded863e49a23f3fe0b14_l3.png)
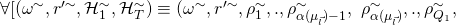
![Rendered by QuickLaTeX.com \mathcal{H}_T^{\sim})] \in \Omega_{\vec{l}}](https://delfr.com/wp-content/ql-cache/quicklatex.com-471b354fce41e6db8974a6e59ed3480c_l3.png) , we have
, we have
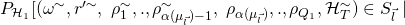
![Rendered by QuickLaTeX.com (\omega^{\sim}, r'^{\sim}, \mathcal{H}_1^{\sim}, \mathcal{H}_T^{\sim}) \in \Omega_{\vec{l}}]\ \geq\ \frac{\nu(k)}{4V_{(Q_1 + Q_T),n}}](https://delfr.com/wp-content/ql-cache/quicklatex.com-14b16b8a95363f41f7c9f234985113a4_l3.png) , and so
, and so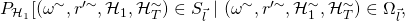
![Rendered by QuickLaTeX.com \rho_1 = \rho_1^{\sim}\ ,..,\ \rho_{\alpha(\mu_{\vec{l}})-1} = \rho_{\alpha(\mu_{\vec{l}})-1}^{\sim})]\ \geq\ \frac{\nu(k)}{4V_{(Q_1 + Q_T),n}}](https://delfr.com/wp-content/ql-cache/quicklatex.com-0cefd7cf52c67df98a7ab659264bff1d_l3.png)
-
![Rendered by QuickLaTeX.com P[(\omega, r', \mathcal{H}_1, \mathcal{H}_T) \in \Omega_{\vec{l}}\ |\ (\omega, r', \mathcal{H}_1, \mathcal{H}_T) \in S_{\vec{l}}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-2a1f54291cd221acc6a8fbbdf8cd43c8_l3.png)
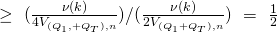
We would like to compute the probability of finding a ![]() successful tuple
successful tuple ![]() given that
given that ![]() was a successful
was a successful ![]() tuple and such that
tuple and such that ![]() . That means finding the following probability:
. That means finding the following probability:
![]()
![]()
From the splitting lemma results, we have a (non-negligible in ![]() ) lower-bound on
) lower-bound on
![]()
![]()
Note however, that ![]() and
and ![]() are generally distinct sets. And so we cannot conclude that
are generally distinct sets. And so we cannot conclude that
![]()
![]()
![]()
![]()
and therefore we cannot conclude that the following quantity is non-negligible in ![]()
![]()
![]()
In order to show that the above quantity is non-negligible in ![]() , we proceed differently. Suppose we can show that the following probability is non-negligible in
, we proceed differently. Suppose we can show that the following probability is non-negligible in ![]()
![]()
This would imply that with non-negligible probability, we can find a tuple that belongs to ![]() (and hence corresponds to a successful forgery) and at the same time belongs to
(and hence corresponds to a successful forgery) and at the same time belongs to ![]() . We can then invoke the splitting lemma result just mentioned, to find a second tuple coresponding to a second forgery and that has the desired properties.
. We can then invoke the splitting lemma result just mentioned, to find a second tuple coresponding to a second forgery and that has the desired properties.
To prove the above, we proceed as follows:
![]()
![]()
![]()
since the ![]() ‘s are disjoint.
‘s are disjoint.
![]()
![]()
![]()
![]()
![]()
(![]() result of splitting lemma above)
result of splitting lemma above)
![]()
(by the claim proven earlier)
![]()
And so we conclude that:
![]()
![]()
![]()
![]()
which is non-negligible in ![]()
So let ![]() be such an index and
be such an index and ![]() such a tuple. From the result above, we know that finding such a
such a tuple. From the result above, we know that finding such a ![]() can be done with non-negligible probability. And since
can be done with non-negligible probability. And since ![]() , we must have
, we must have ![]() . We can then invoke the
. We can then invoke the ![]() consequence of the splitting lemma and write:
consequence of the splitting lemma and write:
![]()
![]()
![]()
![]()
![]()
We still have one last constraint to impose and that is that ![]() . We show that the following quantity is non-negligible:
. We show that the following quantity is non-negligible:
![]()
![]()
To prove this, we use the same technique employed in part 2 and part 4 of this series. Note that if ![]() and
and ![]() are independent events, then we can write:
are independent events, then we can write:
![]()
![]()
And so we get ![]()
This result allows us to write:
![]()
![]()
![]()
![]()
![]()
![]()
(because we chose ![]()
![]() , which is non-negligible in
, which is non-negligible in ![]()
Step 5: The final step uses the 2 forgeries obtained earlier to solve an instance of the Discrete Logarithm (DL) problem. Here is a recap of Step 4 results:
- With non-negligible probability of at least
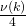 we get a successful tuple
we get a successful tuple 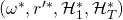 , s.t.
, s.t. 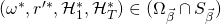 for some vector of indices
for some vector of indices 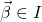 . By running
. By running 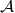 a number of times polynomial in
a number of times polynomial in 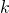 , we can find such a tuple.
, we can find such a tuple. - Once we find such a tuple, we’ve also shown that with non-negligible probability of at least
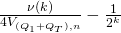 , we can find another successful tuple
, we can find another successful tuple 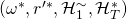 s.t.
s.t. 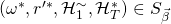 and
and 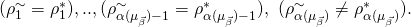
Let ![]() correspond to forgery
correspond to forgery
![]()
and ![]() correspond to forgery
correspond to forgery
![]()
Recall that ![]() is the index of the last query of the form
is the index of the last query of the form ![]() that
that ![]() sends to RO
sends to RO ![]() (
(![]() ). Since the 2 experiments corresponding to the 2 successful tuples have:
). Since the 2 experiments corresponding to the 2 successful tuples have:
- The same random tapes
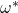 and
and 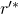
- The same RO
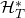
- ROs
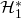 and
and 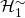 behave the same way on the first
behave the same way on the first 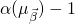 queries,
queries,
we can be confident that the first ![]() queries sent to the 2 ROs
queries sent to the 2 ROs ![]() and
and ![]() are identical. In other words,
are identical. In other words, ![]() . Without loss of generality, let
. Without loss of generality, let ![]() , (where
, (where ![]() ), correspond to the last query of this type sent to RO
), correspond to the last query of this type sent to RO ![]() . That means that
. That means that ![]() is the
is the ![]() query sent to RO
query sent to RO ![]() . We have:
. We have:
![]()
(where (![]() , whenever
, whenever ![]() )
)
![]()
![]()
![]()
(by writing ![]()
Moreover, we have
![]()
(by definition of ![]() in
in ![]() )
)
![]()
(by design of the forgery tuples)
![]()
(by definition of ![]() in
in ![]() )
)
That means that we can solve for ![]() in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that the LSAG signature scheme is secure against EFACM in the RO model.
in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that the LSAG signature scheme is secure against EFACM in the RO model.
5. Security analysis – Exculpability
In part 5 of this series we discussed 2 different notions of exculpability. One of them had to do with the security property of anonymity and the other with the security property of unforgeability. Exculpability in the anonymity sense roughly meant that a signer’s identity can not be established even if her private key gets compromised (i.e., no one can prove that she was the actual signer under any circumstance). This section is concerned with the notion of exculpability from an unforgeability standpoint as described in [2].
The setting is similar to the one previously described in part 5. Suppose ![]() private keys have been compromised in an
private keys have been compromised in an ![]() -ring setting. Let
-ring setting. Let ![]() denote the index of the only non-compromised private key
denote the index of the only non-compromised private key ![]() , and let
, and let ![]() denote the key-image (or tag) associated with the key pair
denote the key-image (or tag) associated with the key pair ![]() . We investigate whether it is likely to produce a valid forgery with key-image
. We investigate whether it is likely to produce a valid forgery with key-image ![]() . In what follows, we show that this can only happen with negligible probability. In essence, this means that a non-compromised honest ring member (by honest we mean a ring member that signs at most once using his private key) does not run the risk of encountering a forged signature that carries his key-image. In the context of Cryptonote, this implies that a non-compromised honest ring member cannot be accused of signing twice using the same key image or tag, and hence is exculpable.
. In what follows, we show that this can only happen with negligible probability. In essence, this means that a non-compromised honest ring member (by honest we mean a ring member that signs at most once using his private key) does not run the risk of encountering a forged signature that carries his key-image. In the context of Cryptonote, this implies that a non-compromised honest ring member cannot be accused of signing twice using the same key image or tag, and hence is exculpable.
Note that since the adversary ![]() has access to the
has access to the ![]() compromised private keys, it can easily calculate their corresponding public keys. Doing so will allow it to identify the public key
compromised private keys, it can easily calculate their corresponding public keys. Doing so will allow it to identify the public key ![]() of the non-compromised ring member. That means that it can determine the index
of the non-compromised ring member. That means that it can determine the index ![]() of the non-compromised member in the ring
of the non-compromised member in the ring ![]() . In order to prove the exculpability of LSAG, we follow an almost identical proof to that of the previous section (i.e., unforgeability vis-a-vis EFACM) and apply the same 5-step approach. The objective is to show that this particular type of forgery would imply the ability to solve the DL of
. In order to prove the exculpability of LSAG, we follow an almost identical proof to that of the previous section (i.e., unforgeability vis-a-vis EFACM) and apply the same 5-step approach. The objective is to show that this particular type of forgery would imply the ability to solve the DL of ![]() . The nuance resides in the specific index
. The nuance resides in the specific index ![]() for which the DL will be solved, as opposed to any other index. This is because we assume that all the other members are compromised and hence their DLs (i.e., private keys) are common-knowledge.
for which the DL will be solved, as opposed to any other index. This is because we assume that all the other members are compromised and hence their DLs (i.e., private keys) are common-knowledge.
Step 1: We proceed by contradiction and assume that there exists a PPT adversary ![]() such that:
such that:
![]()
![]() , for
, for ![]() non-negligible in
non-negligible in ![]()
We refer to the event succeeds in creating a forgery ![]() as
as ![]() . We re-write the above equation as:
. We re-write the above equation as:
![]()
![]() , for
, for ![]() non-negligible in
non-negligible in ![]()
The notation used makes it explicit that ![]() can access the set of compromised keys
can access the set of compromised keys ![]() with
with ![]() excluded. Success is defined as issuing a forged signature with key image or tag equal to
excluded. Success is defined as issuing a forged signature with key image or tag equal to ![]() . (Recall that
. (Recall that ![]() is derived from
is derived from ![]() ).
).
Step 2: The next step consists in building a simulator ![]() such that it:
such that it:
- Does not have access to the private key of any signer.
- Has the same range as the original signing algorithm
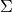 (i.e., they output signatures taken from the same pool of potential signatures over all possible choices of RO functions and respective random tapes
(i.e., they output signatures taken from the same pool of potential signatures over all possible choices of RO functions and respective random tapes 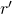 and
and  ).
). - Has indistinguishable probability distribution from that of
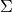 over this range.
over this range.
The simulator ![]() is the same as the one we built in the previous section. The only nuance is that
is the same as the one we built in the previous section. The only nuance is that ![]() does not choose a random index
does not choose a random index ![]() , since
, since ![]() already knows the index of the non-compromised ring member.
already knows the index of the non-compromised ring member.
Step 3: The logical reasoning and procedure are identical to those of the previous section. We conclude that
![]()
![]()
Step 4: Here too, the logical reasoning and procedure are identical to those of the previous section. In particular, we define the following sets in a similar way:
and conclude that:
![]()
![]()
![]() , which is non-negligible in
, which is non-negligible in ![]()
Here ![]() , as before, is an appropriately defined index,
, as before, is an appropriately defined index, ![]() , and
, and ![]() for all
for all ![]() .(
.(![]() denotes the
denotes the ![]() query sent to RO).
query sent to RO).
Step 5: The final step uses the 2 forgeries obtained earlier to solve an instance of the Discrete Logarithm (DL) problem. Here is a recap of Step 4 results:
- With non-negligible probability of at least
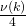 we get a successful tuple
we get a successful tuple 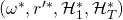 , s.t.
, s.t. 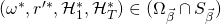 for some vector of indices
for some vector of indices 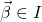 . By running
. By running 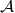 a number of times polynomial in
a number of times polynomial in 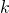 , we can find such a tuple.
, we can find such a tuple. - Once we find such a tuple, we’ve also shown that with non-negligible probability of at least
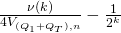 , we can find another successful tuple
, we can find another successful tuple 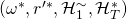 s.t.
s.t. 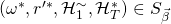 and
and 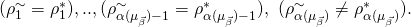
Let ![]() correspond to forgery
correspond to forgery
![]()
and ![]() correspond to forgery
correspond to forgery
![]()
Recall that ![]() is the index of the last query of the form
is the index of the last query of the form ![]() that
that ![]() sends to RO
sends to RO ![]() (
(![]() ). Since the 2 experiments corresponding to the 2 successful tuples have:
). Since the 2 experiments corresponding to the 2 successful tuples have:
- The same random tapes
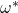 and
and 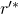
- The same RO
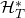
- ROs
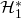 and
and 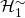 behave the same way on the first
behave the same way on the first 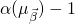 queries,
queries,
we can be confident that the first ![]() queries sent to the 2 ROs
queries sent to the 2 ROs ![]() and
and ![]() are identical. In other words, we have
are identical. In other words, we have
![]()
![]() , and
, and ![]()
Let ![]() , and
, and ![]() . For each
. For each ![]() , we get 2 identical systems of 2 equations dictated by
, we get 2 identical systems of 2 equations dictated by ![]() ‘s verification computation:
‘s verification computation:
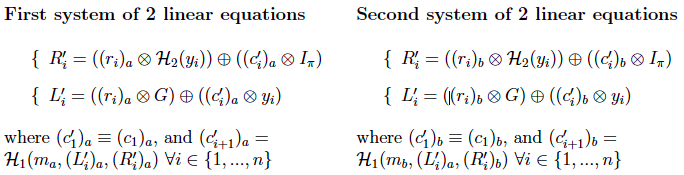
![]() , the first system is a linear system of 2 equations in variables
, the first system is a linear system of 2 equations in variables ![]() and
and ![]() . Similarly, the second system is a linear system of 2 equations in variables
. Similarly, the second system is a linear system of 2 equations in variables ![]() and
and ![]() . The 2 systems are identical with different variable names. Hence, if
. The 2 systems are identical with different variable names. Hence, if ![]() is a unique solution to the first system and
is a unique solution to the first system and ![]() a unique solution to the second, we can be confident that
a unique solution to the second, we can be confident that ![]() and
and ![]() . (Note that when we previously proved resilience against EFACM in section 4, the 2 forged signatures did not necessarily share the same tag
. (Note that when we previously proved resilience against EFACM in section 4, the 2 forged signatures did not necessarily share the same tag ![]() and so the 2 systems of linear equations would have been different from each other). For either system to admit a unique solution, the 2 equations must be linearly independent. We re-write the 2 systems as follows:
and so the 2 systems of linear equations would have been different from each other). For either system to admit a unique solution, the 2 equations must be linearly independent. We re-write the 2 systems as follows:
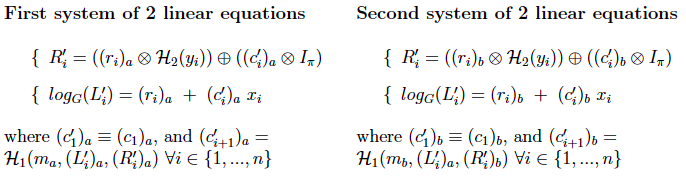
If we multiply the second equation by ![]() (multiplication refers to
(multiplication refers to ![]() ), we see that a sufficient condition for the system to be linearly independent is to have
), we see that a sufficient condition for the system to be linearly independent is to have ![]() . Next, we show that with overwhelming probability, the system of linear equations is indeed independent for all
. Next, we show that with overwhelming probability, the system of linear equations is indeed independent for all ![]() :
:
- Recall that the range of
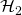 is
is 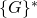 and that the order of
and that the order of 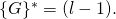
- Therefore,
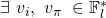 such that
such that 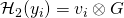 and
and 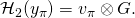
- We can then re-write the sufficient condition as
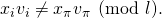
- Note that given
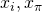 , and
, and 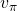 , there is at most one value of
, there is at most one value of 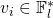 that satisfies
that satisfies 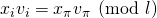 . Otherwise, we would have
. Otherwise, we would have 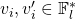 ,
, 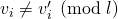 , and
, and 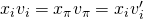 . This would imply that
. This would imply that 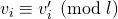 , a contradiction.
, a contradiction. - Noting that each
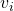 corresponds to a distinct
corresponds to a distinct 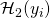 , we conclude that given
, we conclude that given 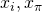 and
and 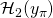 there is at most one
there is at most one 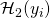 s.t.
s.t. ![Rendered by QuickLaTeX.com [x_i \otimes \mathcal{H}_2(y_i)]\ =\ I_{\pi} \equiv [x_{\pi} \otimes \mathcal{H}_2(y_{\pi})].](https://delfr.com/wp-content/ql-cache/quicklatex.com-494883c25041117c91d57e16a61748f6_l3.png)
- Since
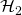 is a RO outputing random values, the probability of getting the right value of
is a RO outputing random values, the probability of getting the right value of 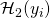 is
is 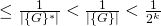 (negligible in
(negligible in 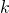 ).
).
![]() , we therefore conclude that with overwhelming probability we have
, we therefore conclude that with overwhelming probability we have ![]() . We can then be confident that the linear system of 2 equations has a unique solution. Hence,
. We can then be confident that the linear system of 2 equations has a unique solution. Hence, ![]() , we have
, we have ![]() , and
, and ![]()
Moreover, by design of the 2 forgeries, we know that there exists one and only one ![]() (corresponding to the
(corresponding to the ![]() query sent to RO
query sent to RO ![]() ) that satisfies
) that satisfies
![]()
(by definition of ![]() in
in ![]() )
)
![]()
(by design of the forgery tuples)
![]()
(by definition of ![]() in
in ![]() )
)
(where ![]() whenever
whenever ![]() )
)
But ![]() , we showed that with overwhelming probability
, we showed that with overwhelming probability ![]() . Therefore, it must be that
. Therefore, it must be that ![]() and so
and so ![]()
Going back to the system of 2 equations associated with ![]() , we write:
, we write:
![]()
That means that we can solve for ![]() in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that the signature scheme is exculpable and secure against
in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that the signature scheme is exculpable and secure against ![]() in the RO model.
in the RO model.
6. Security analysis – Anonymity
In this section, we show that the LSAG scheme satisfies the weaker anonymity definition #2 introduced in part 3 of this series. Note that as we previously observed in part 5, linkable signatures cannot satisfy anonymity definition #1.
More formally, let ![]() be a PPT adversary with random tape
be a PPT adversary with random tape ![]() that takes 4 inputs:
that takes 4 inputs:
- Any message
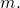
- A ring
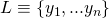 that includes the public key
that includes the public key 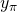 of the actual signer.
of the actual signer. - A list
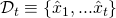 of compromised private keys of ring members (
of compromised private keys of ring members (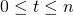 ).
). 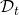 can be empty, and
can be empty, and 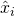 may be different than
may be different than 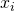 , but
, but 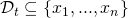
- A valid signature
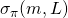 on message
on message 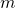 , ring
, ring 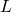 and actual signer private key
and actual signer private key 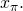
![]() outputs an index in
outputs an index in ![]() that it thinks is the actual signer. Definition # 2 mandates that for any polynomial in security parameter
that it thinks is the actual signer. Definition # 2 mandates that for any polynomial in security parameter ![]()
![]() , we have:
, we have:
![]()
![]()
if ![]() and
and ![]()
![]()
if ![]() or
or ![]()
In the RO model, ![]() can send a number of queries (polynomial in
can send a number of queries (polynomial in ![]() ) to RO
) to RO ![]() and RO
and RO ![]() . The probability of
. The probability of ![]() ‘s success is computed over the distributions of
‘s success is computed over the distributions of ![]() and
and ![]() . Making explicit the dependence on the ROs, definition # 2’s condition becomes:
. Making explicit the dependence on the ROs, definition # 2’s condition becomes:
![]()
![]()
if ![]() and
and ![]()
![]()
![]()
if ![]() or
or ![]()
In order to prove that anonymity holds in the above sense, we proceed by contradiction and rely on the intractability of the Decisional Diffie Hellman problem (DDH for short). (Refer to part 5 for a discussion of DDH). We consider 3 separate cases:
Case 1: ![]() and
and ![]()
Suppose that ![]() in PPT(
in PPT(![]() ) and
) and ![]() non-negligible in
non-negligible in ![]() such that
such that
![]()
![]()
if ![]() and
and ![]()
Recall that since ![]() , one can automatically rule out all the compromised ring members as possible signers (the logic was described in the anonymity section of part 5). One can then limit the guessing range of the identity of the signer to the uncompromised batch of
, one can automatically rule out all the compromised ring members as possible signers (the logic was described in the anonymity section of part 5). One can then limit the guessing range of the identity of the signer to the uncompromised batch of ![]() remaining members.
remaining members.
We now build ![]() PPT(
PPT(![]() ) that colludes with
) that colludes with ![]() to solve the DDH problem.
to solve the DDH problem. ![]() ‘s input consists of 1) The tuple
‘s input consists of 1) The tuple ![]() being tested for DDH, 2) A certain ring size
being tested for DDH, 2) A certain ring size ![]() ( randomly chosen), 3) A number
( randomly chosen), 3) A number ![]() of compromised members (randomly chosen), and 4) A message
of compromised members (randomly chosen), and 4) A message ![]() (randomly chosen).
(randomly chosen).
![]() outputs a tuple consisting of 1) The message
outputs a tuple consisting of 1) The message ![]() , 2) A randomly generated ring
, 2) A randomly generated ring ![]() of size
of size ![]() , 3) A randomly chosen set
, 3) A randomly chosen set ![]() of
of ![]() compromised secret keys, and 4) A not-necessarily valid signature
compromised secret keys, and 4) A not-necessarily valid signature ![]() assigned to ring member
assigned to ring member ![]() s.t.
s.t. ![]()
We let ![]() run the following algorithm:
run the following algorithm:

![]() feeds its output
feeds its output ![]() to
to ![]() . In order for
. In order for ![]() to use its advantage in guessing the signer’s identity, it must be given a valid signature (i.e., a signature that is an element of the range of acceptable signatures over all RO
to use its advantage in guessing the signer’s identity, it must be given a valid signature (i.e., a signature that is an element of the range of acceptable signatures over all RO ![]() . For
. For ![]() to be a valid signature,
to be a valid signature, ![]() must be a DDH instance. Indeed, let
must be a DDH instance. Indeed, let ![]() be partially defined as per the design of
be partially defined as per the design of ![]() . We show that for this particular
. We show that for this particular ![]() , the signature obtained is an element of the range of acceptable signatures. First note that:
, the signature obtained is an element of the range of acceptable signatures. First note that:
If ![]() then we get:
then we get:
Since ![]() is a DDH instance then we necessarily have
is a DDH instance then we necessarily have ![]()
Moreover, recall that ![]() (by design of
(by design of ![]() ). And so
). And so ![]() and
and ![]() . We therefore conclude by induction on
. We therefore conclude by induction on ![]() that
that ![]() ,
, ![]() . In particular,
. In particular, ![]() . This in turn implies that
. This in turn implies that ![]() is a valid signature.
is a valid signature.
On the other hand, if ![]() is not a DDH instance, then
is not a DDH instance, then ![]() and with overwhelming probability
and with overwhelming probability ![]() is not a valid signature.
is not a valid signature.
Recall that ![]() can send queries to
can send queries to ![]() and
and ![]() during execution. It is important to enforce consistency between
during execution. It is important to enforce consistency between ![]() and
and ![]() ‘s query results obtained from RO
‘s query results obtained from RO ![]() and RO
and RO ![]() on the same input. There are no risks of faulty collisions in so far as
on the same input. There are no risks of faulty collisions in so far as ![]() is concerned (by design of
is concerned (by design of ![]() ). However,
). However, ![]() bypasses RO
bypasses RO ![]() and conducts its own backpatching to
and conducts its own backpatching to ![]() . If
. If ![]() such that
such that ![]() queries
queries ![]() on input
on input ![]() , then with overwhelming probability, it will conflict with
, then with overwhelming probability, it will conflict with ![]() ‘s backpatched value causing the execution to halt.
‘s backpatched value causing the execution to halt.
The aforementioned collision must be avoided. In order to do so, we first calculate the probability of its occurence. We assume that during execution, ![]() can make a maximum of
can make a maximum of ![]() queries to RO
queries to RO ![]() .
. ![]() is assumed to be polynomial in the security parameter
is assumed to be polynomial in the security parameter ![]() , since the adversary is modeled as a PPT Turing machine.
, since the adversary is modeled as a PPT Turing machine.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
and so we conclude that:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
whenever ![]() and
and ![]() . Here,
. Here, ![]() is non-negligibale in
is non-negligibale in ![]()
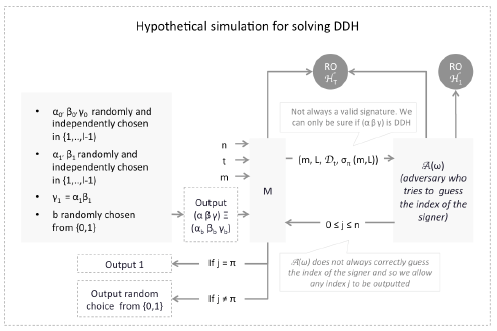
After execution, ![]() returns to
returns to ![]() an integer
an integer ![]() .
. ![]() then outputs 1 if
then outputs 1 if ![]() , or outputs 0/1 with equal probability otherwise. The following diagram summarizes the process:
, or outputs 0/1 with equal probability otherwise. The following diagram summarizes the process:
Using the setting described above, we now calculate the probability of ![]() guessing whether
guessing whether ![]() is DDH or not. The calculation is the same as the one previously conducted in part 5. In what follows we make use of the following notational simplifications:
is DDH or not. The calculation is the same as the one previously conducted in part 5. In what follows we make use of the following notational simplifications:
- We refer to
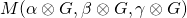 simply as
simply as 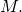
- We refer to
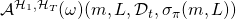 simply as
simply as 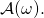
We start by noticing that
![]()
![]()
- Case (
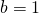 ): In this case,
): In this case, 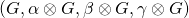 is a DDH instance and so as we saw earlier,
is a DDH instance and so as we saw earlier, 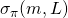 will be a valid signature.
will be a valid signature. 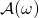 would then use its hypothetical advantage to guess the index of the signer among the
would then use its hypothetical advantage to guess the index of the signer among the 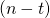 non-compromised ring members. We get:
non-compromised ring members. We get:
![Rendered by QuickLaTeX.com P[M=b|b=1] \geq P[(M=b) \cap (\overline{Col})\ | b=1]](https://delfr.com/wp-content/ql-cache/quicklatex.com-4a3f46a5c0b00a34de88d5762a3b1393_l3.png)
![Rendered by QuickLaTeX.com = P[(M=b) \cap (\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ | b=1]\ +\ P[(M=b) \cap](https://delfr.com/wp-content/ql-cache/quicklatex.com-3bd130ee4eef8f2028d7caa7b809d9ac_l3.png)
![Rendered by QuickLaTeX.com (\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col}) | b=1]](https://delfr.com/wp-content/ql-cache/quicklatex.com-c690cfd6d0eacde0f73ffd9770235c29_l3.png)
![Rendered by QuickLaTeX.com =P[M=b\ |\ (b=1), (\mathcal{A}(\omega) = \pi), (\overline{Col})] \times P[(\mathcal{A}(\omega) = \pi) \cap\ (\overline{Col})\ |\ (b=1)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-6262a19c342043f6a66567670591a422_l3.png)
![Rendered by QuickLaTeX.com +\ P[M=b\ |\ (b=1), (\mathcal{A}(\omega) \neq \pi), (\overline{Col})] \times P[(\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col})\ |\ (b=1)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-450d9b7279bfa610981af4441172d75f_l3.png)
![Rendered by QuickLaTeX.com =1 \times P[(\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ |\ (b=1)] + \frac{1}{2} \times P[(\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col})\ |\ (b=1)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-cb484787ad8347759c1b4c08a8baa82c_l3.png)
(by design of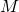 ).
).Since
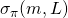 is a valid signature, we have:
is a valid signature, we have:![Rendered by QuickLaTeX.com P[(\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ |\ (b=1)] > \frac{1}{n-t} + \nu(k)](https://delfr.com/wp-content/ql-cache/quicklatex.com-f8a119691dde8c2c9ace4d19b7e5acfc_l3.png)
for non-negligible in
non-negligible in 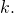
Let
![Rendered by QuickLaTeX.com P[(\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ |\ (b=1)] = \frac{1}{n-t} + \zeta](https://delfr.com/wp-content/ql-cache/quicklatex.com-63627b99494d42217cccfdf82eb88588_l3.png) for some
for some 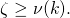
Hence
![Rendered by QuickLaTeX.com P[(\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col})\ |\ (b=1)] = 1-\frac{1}{n-t} - \zeta](https://delfr.com/wp-content/ql-cache/quicklatex.com-175336cf249b7b9cf23612fda63975f7_l3.png) . We get:
. We get:![Rendered by QuickLaTeX.com P[M=b|b=1] \geq 1 \times (\frac{1}{n-t} + \zeta)\ +\ \frac{1}{2}\times(1-\frac{1}{n-t}-\zeta)](https://delfr.com/wp-content/ql-cache/quicklatex.com-ce33d37b8c86f0fc9762d0db5be9b7fe_l3.png)
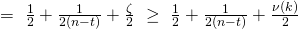
- Case (
 ): In this case, we do not know if
): In this case, we do not know if  is a DDH instance or not, and hence can not be sure whether
is a DDH instance or not, and hence can not be sure whether 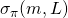 is a valid signature. Consequently,
is a valid signature. Consequently, 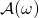 can no longer use its advantage in guessing the index of the signer, because this advantage works only when it is fed a valid signature. We get:
can no longer use its advantage in guessing the index of the signer, because this advantage works only when it is fed a valid signature. We get:
![Rendered by QuickLaTeX.com P[M=b|b=0] \geq P[(M=b) \cap (\overline{Col})\ | b=0]](https://delfr.com/wp-content/ql-cache/quicklatex.com-87e14d6e040cf092772aaa2f97a7219d_l3.png)
![Rendered by QuickLaTeX.com = P[(M=b) \cap (\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ | b=0] + P[(M=b) \cap](https://delfr.com/wp-content/ql-cache/quicklatex.com-d5d330597672c7c8aeecece62a12335d_l3.png)
![Rendered by QuickLaTeX.com (\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col})\ | b=0]](https://delfr.com/wp-content/ql-cache/quicklatex.com-98018d1e8b0dc81212c771865b843c64_l3.png)
![Rendered by QuickLaTeX.com =P[M=b\ |\ (b=0), (\mathcal{A}(\omega) = \pi), (\overline{Col})] \times P[(\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ |\ (b=0)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-f751179bd6aacc4a5dd58244ca7f032a_l3.png)
![Rendered by QuickLaTeX.com +\ P[M=b\ |\ (b=0), (\mathcal{A}(\omega) \neq \pi), (\overline{Col})] \times P[(\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col})\ |\ (b=0)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-f00d23dcb8bed8166c3241eb80f9c501_l3.png)
![Rendered by QuickLaTeX.com =0 \times P[(\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ |\ (b=0)] + \frac{1}{2} \times P[(\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col})\ |\ (b=0)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-6fde90d383ea146db9d54a21985834b4_l3.png)
(by design of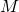 ).
).and since
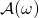 can no longer use its advantage to guess the index of the signer, the best thing it can do is random guessing among non-compromised members. Hence:
can no longer use its advantage to guess the index of the signer, the best thing it can do is random guessing among non-compromised members. Hence:![Rendered by QuickLaTeX.com P[(\mathcal{A}(\omega) = \pi) \cap (\overline{Col})\ |\ (b=0)] = \frac{1}{n-t}](https://delfr.com/wp-content/ql-cache/quicklatex.com-6aacd3ddd8ff1bf108bd28dbdfafd510_l3.png)
and
![Rendered by QuickLaTeX.com P[(\mathcal{A}(\omega) \neq \pi) \cap (\overline{Col})\ |\ (b=0)] = 1 - \frac{1}{n-t}.](https://delfr.com/wp-content/ql-cache/quicklatex.com-5bafab05086d675b3d914e98e704c27e_l3.png)
We get:
![Rendered by QuickLaTeX.com P[M=b|b=0] \geq 0 \times (\frac{1}{n-t})\ +\ \frac{1}{2}\times(1-\frac{1}{n-t}) =\ \frac{1}{2} - \frac{1}{2(n-t)}](https://delfr.com/wp-content/ql-cache/quicklatex.com-80fd9531ecbf9f23daff7e892e4b9775_l3.png)
Putting it altogether, we conclude that:
![]()
![]()
Since ![]() is non-negligible in
is non-negligible in ![]() , the above probability outperforms random guessing. This contradicts the intractability of DDH. Similarly, we can show
, the above probability outperforms random guessing. This contradicts the intractability of DDH. Similarly, we can show
![]()
is also bounded from below. We finally conclude that for any polynomial ![]() :
:
![]()
![]() , if
, if ![]() and
and ![]()
Case 2: ![]() and
and ![]()
In this case, ![]() can check if
can check if ![]() (the key-image or tag of
(the key-image or tag of ![]() ) matches any of the compromised tags
) matches any of the compromised tags ![]() , for
, for ![]() . With overwhelming probability, none of them will match since we proved that the scheme is exculpable and so no one can forge a signature with a tag of a non-compromised member. Proceeding by elimination,
. With overwhelming probability, none of them will match since we proved that the scheme is exculpable and so no one can forge a signature with a tag of a non-compromised member. Proceeding by elimination, ![]() can then conclude that the signer is
can then conclude that the signer is ![]()
Case 3: ![]()
In this case, ![]() can check which of the compromised tags
can check which of the compromised tags ![]() (
(![]() ) matches
) matches ![]() (the key-image or tag of
(the key-image or tag of ![]() ). Only one of them will match (due to exculpability), subsequently revealing the identity of the signer.
). Only one of them will match (due to exculpability), subsequently revealing the identity of the signer.
7. Security analysis – Linkability
Recall that the linkability property means that if a secret key is used to issue more than one signature, then the resulting signatures will be linked and flagged by ![]() (the linkability algorithm)
(the linkability algorithm)
We proved in part 5 of this series that a signature scheme is linkable if and only if ![]() a ring of
a ring of ![]() members, it is not possible to produce
members, it is not possible to produce ![]() valid signatures with pairwise different key-images such that all of them get labeled independent by
valid signatures with pairwise different key-images such that all of them get labeled independent by ![]()
To prove that the LSAG scheme is linkable we follow a reductio ad absurdum approach, similar to the one described in part 5:
- Assume that the LSAG scheme is not linkable.
- The equivalence above would imply that
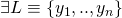 such that it can produce
such that it can produce 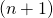 valid signatures with pairwise different key-images (i.e.,
valid signatures with pairwise different key-images (i.e.,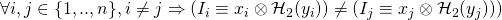 , and such that all of them get labeled independent by
, and such that all of them get labeled independent by 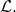
- This means that there must exist a signature (from the set of
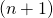 valid signatures) with key-image
valid signatures) with key-image 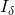 such that
such that 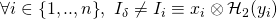 . Denote this signature by
. Denote this signature by 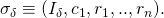
- When verifying the validity of
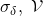 will first compute the following:
will first compute the following:
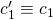
- for all
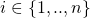 :
:
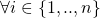 , the system of 2 equations given by
, the system of 2 equations given by 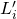 and
and 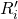 can be equivalently written as:
can be equivalently written as:
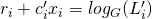
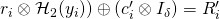
For a given
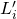 ,
, 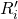 , and
, and 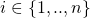 , this constitutes a system of 2 equations in variables
, this constitutes a system of 2 equations in variables 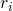 and
and 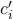 .
.
-
Since
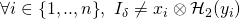 , the system of 2 equations corresponding to each
, the system of 2 equations corresponding to each 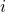 is independent and admits a unique solution
is independent and admits a unique solution 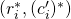 for any given
for any given 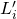 , and
, and 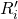 . In particular, that means that the value
. In particular, that means that the value 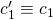 is well defined and equal to
is well defined and equal to 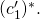
-
By virtue of being a valid signature,
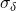 must satisfy
must satisfy 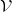 ‘s verification equation. More specifically, it must be that
‘s verification equation. More specifically, it must be that 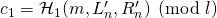 . But RO
. But RO 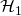 is random by definition. The probability that it outputs a specific value is eqal to
is random by definition. The probability that it outputs a specific value is eqal to  (recall that the range of
(recall that the range of 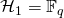 ). Since by design we have
). Since by design we have 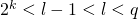 , we conclude that the probability that
, we conclude that the probability that 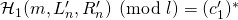 is upper-bounded by
is upper-bounded by 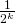 and is hence negligible. In other terms, the probability that
and is hence negligible. In other terms, the probability that 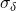 is a valid signature is negligible.
is a valid signature is negligible.
We can then conclude that with overwhelming probability, the ring ![]() can not produce
can not produce ![]() valid signatures with pairwise different key-images and such that all of them get labeled independent by
valid signatures with pairwise different key-images and such that all of them get labeled independent by ![]() . The LSAG scheme as we introdued it is hence linkable.
. The LSAG scheme as we introdued it is hence linkable.
References
[1] A. Back. Ring signature efficiency. 2015.
[2] E. Fujisaki and K. Suzuki. Traceable ring signatures. Public Key Cryptography, pages 181-200, 2007.
[3] J. K. Liu, V. K. Wei, and D. S. Wong. Linkable spontaneous anonymous group signature for ad hoc groups. ACISP, Lecture Notes in Computer Science(3108):325-335, 2004.
[4] S. Noether and A. Mackenzie. Ring condential transactions. Monero Research Lab, 2016.
Tags: anonymity, Group, Linkable, LSAG, Monero, Privacy, ring signature

No comments
Comments feed for this article
Trackback link: https://delfr.com/lsag-signature-scheme-monero-6-10/trackback/