1. Introduction
The previous nine parts introduced Monero’s privacy and confidentiality attributes in so far as senders’ identities and transaction amounts were concerned. This part focuses on privacy with respect to the recipients of funds. To that end, we introduce the stealth address system [8] to ensure that any two transactions remain unlinkable, i.e., can not be proven to be destined to the same entity.
We divide this part into two sections. The first is an overview of some of the anonymity limitations of Bitcoin. The second introduces Cryptonote’s stealth address system which when coupled with ringCT, ensures a highly anonymous and confidential environment.
2. On Bitcoin’s anonymity … or lack thereof
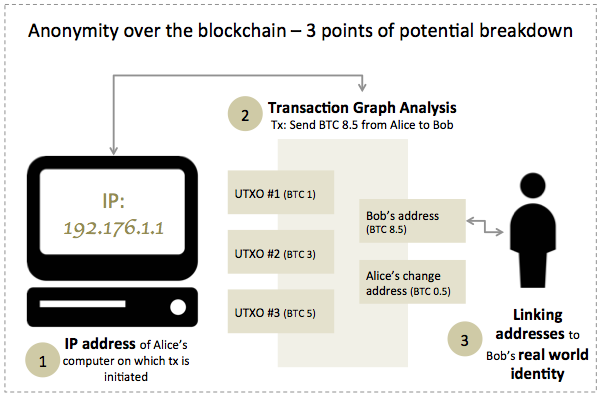
In what follows, we describe two avenues that can be used separately or jointly to conduct a deanonymization attack on Bitcoin users. The first has to do with the propagation mechanisms of Bitcoin transactions over the network, and the second with the structure of a transaction. In addition, we describe some common practices that help an attacker link a Bitcoin address to a real-world identity.
Transaction propagation and IP revelation: The Bitcoin network is a peer to peer network (P2P) where members are connected to other members via an unencrypted Transmission Control Protocol (TCP) channel. In essence, TCP establishes a reliable connection between hosts that communicate using the Internet Protocol (IP), in order to transmit byte-format information between relevant applications. Members of the bitcoin P2P network, also known as nodes, maintain a list of the IP addresses of each host and node that connects to them. Some of these nodes are open to incoming connections while others do not accept new connections beyond the ones they already have. At the time of writing, there were circa ![]() reachable nodes [1]. Note that this figure refers to accessible nodes not hiding behind a firewall, and that the cumulative number of nodes is likely to be much higher.
reachable nodes [1]. Note that this figure refers to accessible nodes not hiding behind a firewall, and that the cumulative number of nodes is likely to be much higher.
When a Bitcoin transaction is created, it is shared with all the nodes that the originating host (e.g., computer) connects to. The transaction is subsequently propagated to the remaining nodes in a cascade fashion whereby each one sends it to its sub-network of connected peers. Recall that each node maintains a list of the IP addresses of hosts that connect to it. Consequently, if a node could confirm that its incoming connection was actually the originator of the transaction (as opposed to being a mere intermediary), it could look-up the IP address associated with it and match it to the transaction. Clearly, this would jeopardize Bitcoin’s presumed anonymity.
The above attack could be achieved in principle and has been analyzed in e.g., [2]. One way would be for the attacker to connect to a statistically significant number of the network’s nodes, such that when the attacker detects a new transaction (i.e., never seen before) from an incoming connection, it can assume with a certain degree of confidence that it corresponds to the originating host. The attacker could then match the host’s IP to that particular transaction. There are ways to mitigate a possible IP breach, including e.g., the use of a VPN or a Tor browser to connect to the Bitcoin network. However, both have limitations and the interested reader could consult e.g., [3] for information about the shortcomings of a Tor connection.
The IP exposure threat is not limited to Bitcoin. It applies to other blockchain-based platforms including Monero. To address this risk, the Monero community of developers is working on the implemention of Kovri. At a high level, it is an anonymity technology built on the Invisible Internet Project (I2P) that uses sophisticated routing techniques to conceal the user’s geographical and IP addresses [5]. (Note that we did not discuss Kovri’s details in this series. It warrants an article in its own right)
Transaction graph analysis and clustering: A Bitcoin transaction consists of transfering control from one entity to another. The notion of control refers to the authority granted to an entity to unlock a certain value or amount. A transaction of BTC 1 from Alice to Bob means that the control over spending that particular BTC 1 has moved from Alice to Bob. Bob can now spend it (or a portion of it) whenever he pleases. In essence, a Bitcoin transaction consists of:
- A set of unspent previous transaction outputs known as UTXOs. Each one contains an amount, the control over which has been transferred from a previous entity to the one initiating the current transaction. These UTXOs (one or more) constitute the input to the transaction. As a result, one could define a Bitcoin transaction as a state transition in the UTXO set.
- One or more recipient addresses who will be given spending control over the UTXOs serving as input in the current transaction. A recipient address acts as a pseudonym for an actual person or entity. As long as the link between the pseudonym and the actual identity is not revealed, the recipient is safe. However, this is usually a difficult endeavour as we will see later.
- An amout specifying the value of BTC to be transferred to each recipient.
Bitcoin transaction information including inputs, outputs and amounts are made available on the blockchain. An important advantage of this transparency is that adequate nodes can validate honest transactions and reject instances of double spending and fraud. However, it also weakens the anonymity of users. In particular, anyone can leverage open information to cluster Bitcoin addresses that belong to the same user. By tying any of these addresses to the user’s real identity, an attacker would also be tying the full cluster. This grouping can be done through a transaction graph analysis [6], [7]. Some simple clustering techniques include:
- UTXO address grouping: All input addresses corresponding to UTXOs used in a given transaction are under the control of the same user. They can hence be clustered and tied to the sender’s bitcoin address.
- Change address analysis: Bitcoin transaction output amounts are indivisible. That means that everytime a UTXO is selected as a source of fund, its full amount must be consumed. In case the amount is larger than what needs to be transferred, a change address is created. As a consequence, the full UTXO amount gets spent on two or more addresses:
- One or more address(es) for the intended recipient(s) (one address per recipient).
- A change address associated with the sender.
The sum total of UTXO amounts must be greater than or equal to what is transacted. Since it is difficult to ensure equality in most cases, the UTXO amount is usually strictly greater than the transacted one. As a result, change addreses are very common.
Under certain circumstances, it is relatively feasible to identify the change address in a given transaction and to cluster it with the sender’s address. Suppose that the sender engages in the practice of generating new receiving addresses whenever he receives new funds, while his intended recipients do not. Without loss of generality, suppose that the current transaction contains two outputs, one for the recipient and a change address returned to the sender. The change address is a brand new address since it is destined to the sender who creates new receiving addresses. The recipient adress on the other hand is not new. Under these circumstances, an attacker that detects exactly one transaction output address that never existed before can reasonably assume that it is the change address and cluster it with that of the sender.
We observe that clustering in this case was possible because the network knows the address of the sender with certainty. In section 3 below, we introduce Cryptonote’s stealth address system that assigns unique receiving addresses for new transactions. Among other things, Monero differs from Bitcoin in that the sender’s UTXO addresses are hidden in a ring (refer to part 7 and part 8). Consequently, the aforementioned clustering becomes overhelmingly unlikely to achieve with Monero.
There are some mitigation techniques to strengthen anonymity in so far as the transaction structure is concerned, but their effectiveness is not always guaranteed:
- One technique consists in using brand new addresses every time one receives new funds. Hierarchical Deterministic (HD) wallets do that automatically. However, we saw that under some circumstances, this does not necessarily increase anonymity.
- Another technique consists in breaking the existing relationship betwen a transaction’s input(s) and output(s) and reconstructing a new one that maintains the transaction amount, net of a processing fee. Services that fulfill this task are known as coin mixers or tumblers. The practical origin of coin-mixing is traced back to Greg Maxwell’s CoinJoin algorithm [4]. Mixers come in two flavors: centralized (e.g., bitmixer.io, helix) and decentralized (e.g., JoinMarket, Jumblr). It is worth noting that centralized mixers suffer from two shortcomings:
- They know each transaction’s input(s) and output(s) addresses and hence do not completely remove the anonymity threat.
- Users send their BTCs to the mixer for re-processing and hence must trust the centralized service not to steal them.
Linking addresses to real-world identity Transaction graph analysis reveals insightful connections at the level of inputs and outputs that allowed targeted clustering, but did not help in establishing a link between a cluster member (i.e., a Bitcoin address) and its real-world counterpart. However, it is relatively feasible to establish such a link. In what follows, we highlight three practices that facilitate it. When coupled with clustering analysis, this could reveal significant insight into the wealth and activity of individuals or entities, a consequence that a number of users might not be comfortable with:
- Mentioning on an online platform (or other media), a name (or any other personal identifier) alongside a relevant bitcoin address.
- Registering and buying Bitcoins on a centralized exchange. Most exchanges that allow the purchase of Bitcoins for fiat currency are required to comply with anti money laundering regulations. As a result, any new subscriber must provide personal information including e.g., a valid government ID, an address, a utility bill, a bank account number. One way to mitigate this is to purchase BTC offline using cash, which might be logistically more challenging.
- Buying with BTC at a point of sale. If the seller requires an address (e.g., for the purpose of shipping goods) or other personal information, the Bitcoin address will be linked to the customer’s identity, hence threatening her anonymity.
3. Monero’s stealth address system
Some individuals might not care about anonymity, in which case the above limitations may be discarded. For the others however, mitigating anonymity threats on the Bitcoin network are likely to prove challenging. Monero’s value proposition is to offer a more anonymous and confidential platform that does not require the user to engage in additional mitigation techniques:
- The IP exposure threat is currently being addressed through Kovri as briefly mentioned earlier.
- The transaction graph analysis is made obsolete in Monero because:
- Linking transaction inputs and change addresses to a specific sender cannot be done with certainty since senders are hidden in a ring structure making them anonymous (refer to part 7).
- Estimating the wealth held by a certain cluster of addresses cannot be achieved since amounts are made confidential through the use of Pedersen Commitments and ringCT (refer to part 8 and part 9)
- Transaction activity analysis with respect to a particular receiving address cannot be completed since each transaction is automatically associated with a unique receiving address known as a stealth address. The stealth address was introduced in Cryptonote’s original paper [8] to make it extremely challenging to prove that any two outgoing transactions were sent to the same person. This in turn guarantees their unlinkability.
By design, a Monero user is associated with a secret key pair ![]() only known to her, and a corresponding public key pair
only known to her, and a corresponding public key pair ![]() that can be publicly shared. Monero keys are hence twice as long as their Bitcoin counterparts. The larger size requirement is tied to the stealth address system as will be explained shortly. We refer to
that can be publicly shared. Monero keys are hence twice as long as their Bitcoin counterparts. The larger size requirement is tied to the stealth address system as will be explained shortly. We refer to ![]() as the viewing key and
as the viewing key and ![]() as the spending key, for reasons that will become obvious in what follows.
as the spending key, for reasons that will become obvious in what follows.
The cryptographic constructs underlying the stealth address system are all built on the same algebraic structure introduced in earlier parts. In particular, we let ![]() be a large finite group generated by the same elliptic curve introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic). The curve’s equation is given by:
be a large finite group generated by the same elliptic curve introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic). The curve’s equation is given by:
![]()
For completeness purposes, we recall that the above equation is a polynomial over ![]() where
where ![]() is a very large prime and
is a very large prime and ![]() is a pre-defined element of
is a pre-defined element of ![]() . We simplify the notation and refer to the group generated by this elliptic curve as
. We simplify the notation and refer to the group generated by this elliptic curve as ![]() . We also observe the following:
. We also observe the following:
- Elements of
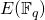 are pairs
are pairs 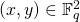 that satisfy the above equation.
that satisfy the above equation. - Elliptic curve groups in general and
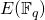 in particular have a well defined addition operation that we denote by
in particular have a well defined addition operation that we denote by 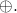
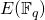 contains a special element
contains a special element 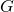 (not necessarily unique) that we refer to as the base point. The base point has order
(not necessarily unique) that we refer to as the base point. The base point has order  , where
, where 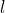 is a very large prime. That means that adding
is a very large prime. That means that adding 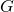 to itself
to itself 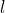 times yields the identity element
times yields the identity element  of
of 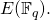 In other terms,
In other terms, 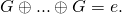 We simply write
We simply write 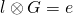 (the notation
(the notation  serves as a reminder that this is scalar multiplication associated with
serves as a reminder that this is scalar multiplication associated with 
- We let
 denote the group generated by
denote the group generated by 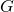 under the
under the  operation of
operation of 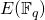 . We also let
. We also let 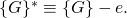
- Solving the Discrete Logarithm (DL) problem on
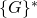 (and more generally on
(and more generally on 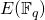 ) is thought to be intractable.
) is thought to be intractable.
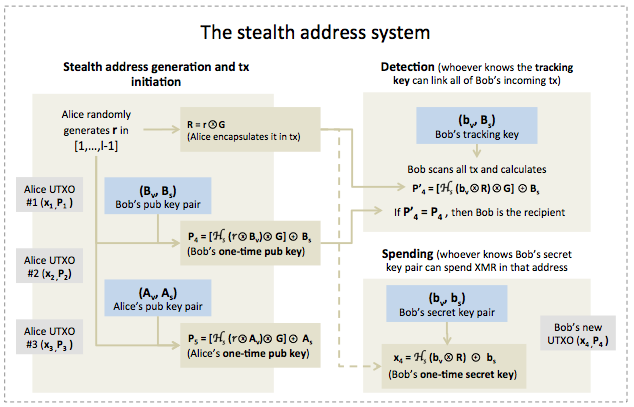
A stealth address is a unique address derived from a one-time public key that senders automatically generate on behalf of their intended receivers. As a result, any transaction is always characterized by a unique receiving address. To generate a stealth address, the sender relies on two pieces of information:
- A random scalar
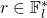 used to generate a shared secret only known to the sender and to the recipient.
used to generate a shared secret only known to the sender and to the recipient. - The public key pair
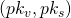 of the recipient.
of the recipient.
Suppose Alice wants to send a certain amount of XMRs to Bob. Without loss of generality, suppose that Alice will transfer her spending control over XMRs locked in her UTXOs #1 to Bob. Clearly Alice knows the private key associated with UTXO #1 and can sign it and conceal the amount using ringCT (refer to part 9). However, Alice needs to know the recipient address. To that end, she will engage in an address creation process generated from a unique one-time public key specific to the current transaction. Assume that Bob’s public key pair is ![]() and his corresponding secret key pair is
and his corresponding secret key pair is ![]() Alice does the following:
Alice does the following:
- Generate a shared secret: The initial objective of the sender is to create a piece of information only known to her and to the recipient. The constraint is that the secret must be created and enforced even if the underlying communication channel is not secure. One way of achieving this is through a Diffie Hellman exchange:
- Generate a random scalar
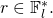
- Calculate its corresponding public key
 (
(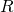 is publicly shared as part of the transaction to be).
is publicly shared as part of the transaction to be). - Compute the shared secret
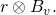 Indeed,
Indeed, 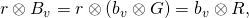 which is also known to Bob since he knows
which is also known to Bob since he knows 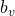 and can access the published value of
and can access the published value of 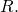 However, anyone who does not know
However, anyone who does not know 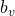 or
or  will not be able to do better than random guessing the value of the shared secret. Moreover, with overwhelming probability, no one can learn the values of
will not be able to do better than random guessing the value of the shared secret. Moreover, with overwhelming probability, no one can learn the values of 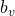 or
or  since this involves solving the DL problem (thought to be hard on elliptic curve groups).
since this involves solving the DL problem (thought to be hard on elliptic curve groups).
- Generate a random scalar
- Create the stealth address: Alice calculates the one-time public key:
![Rendered by QuickLaTeX.com P \equiv [\mathcal{H}_s(r \otimes B_v)\ \otimes\ G]\ \oplus\ B_s](https://delfr.com/wp-content/ql-cache/quicklatex.com-3d821d8300f11f574488ef8f605d92b5_l3.png)
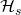 is a hash function (in Monero it refers to keccak-256) that takes an element of
is a hash function (in Monero it refers to keccak-256) that takes an element of 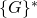 and outputs a scalar in
and outputs a scalar in 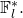 Since this key determines the destination address, an important question is whether it is truly unique. To answer it, we quantify the probability that a stealth address pair collide. Note that the one-time public key is a function of two parameters:
Since this key determines the destination address, an important question is whether it is truly unique. To answer it, we quantify the probability that a stealth address pair collide. Note that the one-time public key is a function of two parameters:- The random parameter
 that Alice generated.
that Alice generated. - The public key pair of the recipient. In the case of Bob, it is
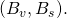
The two scenarios under which a stealth address collision occurs are:
- Alice conducts a second transaction destined to Bob, but uses the same random parameter
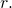 Assuming that the sender always generates new random elements when conducting new transactions, the probability of the same
Assuming that the sender always generates new random elements when conducting new transactions, the probability of the same  being chosen a second time is equal to
being chosen a second time is equal to 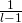 (since
(since  is a random scalar
is a random scalar 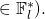 This is clearly negligible in the security parameter
This is clearly negligible in the security parameter 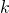 , since
, since 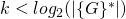 by design (refer to parts 5, 6, and 7 for a review of the security parameter).
by design (refer to parts 5, 6, and 7 for a review of the security parameter). - Alice conducts two transactions. The first destined to Bob with public key pair
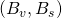 and random parameter
and random parameter 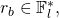 and the second destined to Carol with public key pair
and the second destined to Carol with public key pair 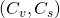 and random parameter
and random parameter 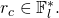 A collision occurs if
A collision occurs if
![Rendered by QuickLaTeX.com [\mathcal{H}_s(r_b \otimes B_v)\ \otimes\ G]\ \oplus\ B_s\ = [\mathcal{H}_s(r_c \otimes C_v)\ \otimes\ G]\ \oplus\ C_s](https://delfr.com/wp-content/ql-cache/quicklatex.com-e7a20cb0aa69fc686fb9082ea3a57003_l3.png)
Given the random nature of the hash function
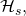 the probability that the two quantities are equal is given by
the probability that the two quantities are equal is given by 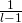 since the range of
since the range of 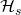 is
is 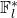 . This quantity is negligible in security parameter
. This quantity is negligible in security parameter 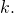
- The random parameter
We conclude that the probability of stealth address collision is negligible. Consequently, we are justified in assuming that the procedure yields unique addresses.
On the receiving end, Bob has two crucial tasks:
- Detect that he is the legitimate owner of the one-time public key.
- Recover the private key associated with this one-time public key in order to spend its content in a future transaction.
Detection: All Monero users actively listen to every transaction on the network and calculate:
![]()
In the case of Bob, this is equivalent to:
![]()
If ![]() matches
matches ![]() then the listener assumes that the transaction is destined to him and that he is the legitimate owner (the probability that at least two listeners compute the same value is negligible as we saw earlier). Anyone who has knowledge of the pair
then the listener assumes that the transaction is destined to him and that he is the legitimate owner (the probability that at least two listeners compute the same value is negligible as we saw earlier). Anyone who has knowledge of the pair ![]() can perform the calculation and conclude that Bob is the intented recipient. This pair is refered to as a tracking key and
can perform the calculation and conclude that Bob is the intented recipient. This pair is refered to as a tracking key and ![]() is known as the view key (hence the subscript
is known as the view key (hence the subscript ![]()
One implication is that if Bob does not have the computational capacity to actively listen on the network, he could delegate that process to a third party by sharing his tracking key. Another implication is that Bob could release his tracking key to an auditor or to a court of law in case of a subpoena for them to check all his incoming transactions. Clearly this renders all of Bob’s incoming addresses linkable, significantly reducing his anonymity.
Spending: Unlinkability is not tied to spendability. By releasing the tracking key, Bob is not relinquishing spending control over the XMRs that he received. This is because spendability requires knowledge of the secret key associated with
![]()
The information content of the tracking key ![]() is not enough to calculate it. Indeed, the secret key is given by
is not enough to calculate it. Indeed, the secret key is given by
![]()
which requires knowledge of ![]() The quantity
The quantity ![]() is known as the spending key, and
is known as the spending key, and ![]() as the one-time private key associated with the one-time public key
as the one-time private key associated with the one-time public key ![]()
The two functions of detecting ownership and spending funds justfy the usage of the dual key structure in Monero and hence the need to have addresses twice as long as in Bitcoin. We summarize below the stealth address construct:
References
[1] Bitnode – bitcoin reachable nodes.
[2] A. Biryukov, D. Khovratovitch, and I. Pustogarov. Deanonymisation of clients in bitcoin p2p network. ACM Conference on Computer and Communications Security, 2014.
[3] A. Biryukov and I. Pustogarov. Bitcoin over tor isn’t a good idea. IEEE Symposium on Security and Privacy, 2015.
[4] G. Maxwell. Coinjoin.
[5] Monero. Kovri.
[6] F. Reid and M. Harrigan. An analysis of anonymity in the bitcoin system. SocialCom/PASSAT, IEEE, pages 1318{1326, 2011.
[7] D. Ron and A. Shamir. Quantitative analysis of the full bitcoin transaction graph. IACR Cryptology ePrint Archive, 2012.
[8] N. Van Saberhagen. Cryptonote 2.0., 2013.
Tags: anonymity, Monero, one-time private key, one-time public key, spend key, Stealth, tracking key, unlinkable, view key

No comments
Comments feed for this article
Trackback link: https://delfr.com/stealth-address-moneros-part-10/trackback/