1. Introduction
Monero stands out from other cryptocurrencies in its ability to hide the signer, conceal the transaction amount, and protect the identity of the recepient. Parts 1, 2, 3, 4, 5, and 6 helped us build the foundation to better understand and appreciate the security properties of ring signatures (albeit in the RO model). This part (introduction to MLSAG), as well as part 8 and part 9 will focus on Monero’s privacy in so far as the signer’s identity and the transaction amount are concerned. Part 10 will introduce stealth addresses as a mechanism to protect the identity of the fund’s recipient.
In order to describe how a Monero transaction hides both the signer’s identity and the amount of the transaction, we introduce 2 additional concepts:
- A generalization of the LSAG signature (introduced in part 6) to allow each member of the ring to have a key-pair vector
![Rendered by QuickLaTeX.com [(pk_1,sk_1),.,(pk_n,sk_n)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-fc575a1ec24eb1df1f27e6a1f8aa72c1_l3.png) instead of only one pair
instead of only one pair 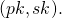
- A particular map known as the Pedersen Commitment that will be used to hide transaction amounts while allowing the network to check that input and output amounts always balance out.
Recall that by proving that a digital signature scheme was unforgeable, one gets the assurance that only the signing algorithm ![]() associated with a given ring member can produce a valid signature (i.e., verified by
associated with a given ring member can produce a valid signature (i.e., verified by ![]() ). Any other procedure that bypasses
). Any other procedure that bypasses ![]() will result in a failed attempt of forgery with overwhelming probability. We note the following about the verification process of
will result in a failed attempt of forgery with overwhelming probability. We note the following about the verification process of ![]() :
:
- In a “non-ring” setting, the verification is done using a particular public key
 . The validation of a given signature proves that the signer of the message (in this case user
. The validation of a given signature proves that the signer of the message (in this case user  ) knows the secret key
) knows the secret key 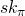 associated with
associated with  . Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (
. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (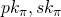 ) signed the message.
) signed the message. - In a ring setting, the verification is conducted using a public key vector
![Rendered by QuickLaTeX.com L \equiv [pk_1,...,pk_{\pi},...,pk_n]](https://delfr.com/wp-content/ql-cache/quicklatex.com-664318b6a8929cb965e54b90a242eb5f_l3.png) known as a ring. This vector is used to conceal the identity of the signer. The validation of a given signature proves that the the signer of the message (in this case user
known as a ring. This vector is used to conceal the identity of the signer. The validation of a given signature proves that the the signer of the message (in this case user  ) knows the secret key associated with one of the public keys in
) knows the secret key associated with one of the public keys in 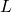 . Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (
. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (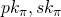 ) signed the message, for some index
) signed the message, for some index  that no one other then the actual signer knows.
that no one other then the actual signer knows. -
The ring setting can be generalized further by allowing each ring member
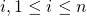 to have a key-pair vector of length
to have a key-pair vector of length 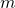 , given by
, given by ![Rendered by QuickLaTeX.com [(pk_{i}^1, sk_{i}^1),...,(pk_{i}^m, sk_{i}^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-9bbb0cc254c0adea6e1b0338b75135b0_l3.png) , as opposed to a unique key pair
, as opposed to a unique key pair 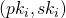 . In this setting, the verification is conducted using a public key matrix
. In this setting, the verification is conducted using a public key matrix![Rendered by QuickLaTeX.com \[PK= \begin{bmatrix} pk_1^1 & ... & pk_{\pi}^1 & ... & pk_n^1 \\ ... & ... & ... & ... & ...\\ pk_1^m & ... & pk_{\pi}^m & ... & pk_n^m \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-753948876edb3252b45709a2a05f6024_l3.png)
The validation of the signature proves that the signer knows the secret key associated with each one of its public keys. In other terms, there exists a column in
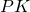 (say column
(say column  ) such that the signer knows the secret key associated with each public key appearing in that column. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair vector
) such that the signer knows the secret key associated with each public key appearing in that column. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair vector ![Rendered by QuickLaTeX.com [(pk_{\pi}^1,sk_{\pi}^1),...,(pk_{\pi}^m,sk_{\pi}^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-c90b77b48be04d2c4194915758b84bbc_l3.png) signed the message, for some index
signed the message, for some index  (that no one other then the actual signer knows).
(that no one other then the actual signer knows).
2. The MLSAG scheme
The MLSAG signature scheme is a generalization of the LSAG scheme encountered earlier in part 6. It was introduced by Shen Noether in his 2016 paper entitled “Ring Confidential Transactions” [2]. MLSAG security analysis closely mirrors that of the LSAG scheme. Although the security proofs are similar, we will go over them again in detail to highlight the nuances pertaining to the generalization.
Similar to the LSAG version, MLSAG is built on a group ![]() of prime order
of prime order ![]() and uses 2 statistically independent ROs:
and uses 2 statistically independent ROs:
We carry forward all the notation used in the Cryptonote scheme and the LSAG scheme. In particular, we conduct arithmetic in the subgroup ![]() of the elliptic curve group
of the elliptic curve group ![]() introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic).
introduced in part 5 (refer to the post entitled Elliptic Curve Groups for an introduction to this topic).
With a slight divergence from [2], we first introduce a hash function ![]() before we define
before we define ![]() . The reason is the same as the one we previously articulated in part 5 and part 6 and will be highlighted in section 4 when we build the signing simulator to prove MLSAG’s resilience against EFACM.
. The reason is the same as the one we previously articulated in part 5 and part 6 and will be highlighted in section 4 when we build the signing simulator to prove MLSAG’s resilience against EFACM.
![]() takes an
takes an ![]() and outputs a tuple
and outputs a tuple ![]() . Here
. Here ![]() is a random element chosen according to a uniform distribution over
is a random element chosen according to a uniform distribution over ![]() . We then let
. We then let ![]() . So
. So ![]() , takes an element
, takes an element ![]() and returns an element
and returns an element ![]() where
where ![]() is randomly chosen in
is randomly chosen in ![]()
Note that [2] defines ![]() as a map from
as a map from ![]() to
to ![]() . Here we restricted the domain and the range to
. Here we restricted the domain and the range to ![]() instead. This is because in our exposition,
instead. This is because in our exposition, ![]() is strictly applied to public keys as opposed to any element of
is strictly applied to public keys as opposed to any element of ![]() . Public keys are elements of
. Public keys are elements of ![]() that are scalar multiples of the base point
that are scalar multiples of the base point ![]() . Moreover, the scalar is never equal to order(
. Moreover, the scalar is never equal to order(![]() )
) ![]() (we impose this constraint when we introduce the key generation algorithm
(we impose this constraint when we introduce the key generation algorithm ![]() ). We are then justified in restricting the domain to
). We are then justified in restricting the domain to ![]() . The range is arbitrarily defined to be
. The range is arbitrarily defined to be ![]() , which is permissible since it preserves the injective nature of the map.
, which is permissible since it preserves the injective nature of the map.
The MLSAG scheme is defined by a set of 4 algorithms:
- The key generation algorithm
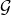 }. On input
}. On input 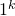 , the MLSAG generation algorithm produces a key-pair vector
, the MLSAG generation algorithm produces a key-pair vector
![Rendered by QuickLaTeX.com [(sk^1,pk^1),...,(sk^m,pk^m)] \equiv [(x^1,y^1),...,(x^m,y^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-cac94a2d7d486f34ffa2aaa2b1a699ec_l3.png)
of matching secret and public keys.
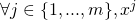 is randomly chosen in
is randomly chosen in 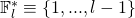 , and
, and 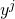 is calculated as
is calculated as 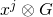 . (Note that
. (Note that  and
and 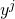 are both elements of
are both elements of  while
while 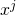 is an element of
is an element of 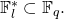 (
(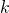 is the security parameter that by design we request to satisfy
is the security parameter that by design we request to satisfy 
In addition to the
![Rendered by QuickLaTeX.com [(x^1,y^1),...,(x^m,y^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-2cb7049d1bf3fe8faa0a55132733e6a3_l3.png) key-pair vector,
key-pair vector, 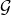 computes
computes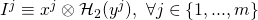
![Rendered by QuickLaTeX.com I \equiv [I^1,...,I^j]](https://delfr.com/wp-content/ql-cache/quicklatex.com-662798aad1116198001165a9395b5356_l3.png) is known as the key image vector (or tag vector). It is signer-specific since it depends only on the signer’s private and public keys. It allows the ring linkability algorithm
is known as the key image vector (or tag vector). It is signer-specific since it depends only on the signer’s private and public keys. It allows the ring linkability algorithm  to test for independence between different MLSAG signatures.
to test for independence between different MLSAG signatures.  is modeled as a PPT Turing machine.
is modeled as a PPT Turing machine.Suppose we have a ring of
 members, each with
members, each with  keys as described above. The objective of the MLSAG scheme is two-fold:
keys as described above. The objective of the MLSAG scheme is two-fold:- To demonstrate that one of the signers knows all the secret keys associated with her key-pair vector.
- To ensure that if the signer uses at least one of their
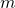 secret keys in a different MLSAG signature, then the 2 MLSAG signatures will be flagged as linked and proper measures taken.
secret keys in a different MLSAG signature, then the 2 MLSAG signatures will be flagged as linked and proper measures taken.
-
The ring signing algorithm
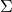 . Suppose a user
. Suppose a user 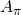 decides to sign a message
decides to sign a message 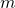 on behalf of the ring
on behalf of the ring 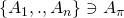 .
. 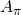 has key-pair vector and key-image vector respectively given by:
has key-pair vector and key-image vector respectively given by:![Rendered by QuickLaTeX.com [(x_{\pi}^1, y_{\pi}^1),.,(x_{\pi}^m, y_{\pi}^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-a69ae8731687ee35426c0c89f110b958_l3.png)
![Rendered by QuickLaTeX.com I_{\pi} \equiv [(x_{\pi}^1 \otimes \mathcal{H}_2(y_{\pi}^1)),...,(x_{\pi}^m \otimes \mathcal{H}_2(y_{\pi}^m))]](https://delfr.com/wp-content/ql-cache/quicklatex.com-5aed2a5e2499a91c2666ad80dd0448c7_l3.png)
Moreover, the public key matrix associated with the ring of users is given by:
![Rendered by QuickLaTeX.com \[ PK= \begin{bmatrix} pk_1^1 & ... & pk_{\pi}^1 & ... & pk_n^1 \\ ... & ... & ... & ... & ...\\ pk_1^m & ... & pk_{\pi}^m & ... & pk_n^m \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-bcae18f5dea2d5978196cc08abb8e0fe_l3.png)
MLSAG’s
 does the following:
does the following: , choose random
, choose random 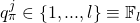 . Assign:
. Assign:
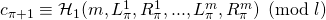
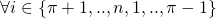 :
:
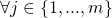 , choose random
, choose random 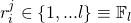 . Assign:
. Assign:
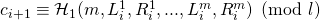 , where
, where 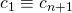
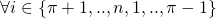 , set
, set 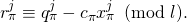 Here
Here 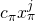 denotes regular scalar multiplication in modulo
denotes regular scalar multiplication in modulo  arithmetic.
arithmetic.  outputs a signature
outputs a signature

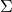 is a PPT algorithm. We note that one drawback of the MLSAG scheme is the size of the signature. An increase of the ring size by one unit corresponds to an increase of
is a PPT algorithm. We note that one drawback of the MLSAG scheme is the size of the signature. An increase of the ring size by one unit corresponds to an increase of 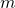 units in the size of the signature. This constraint limits the usage of large ring sizes in practice.
units in the size of the signature. This constraint limits the usage of large ring sizes in practice.
- The ring verification algorithm
 . Given a message
. Given a message  , a pubic key matrix of the ring members given by:
, a pubic key matrix of the ring members given by:
![Rendered by QuickLaTeX.com \[PK=\begin{bmatrix}pk_1^1 & ... & pk_{\pi}^1 & ... & pk_n^1 \\... & ... & ... & ... & ...\\pk_1^m & ... & pk_{\pi}^m & ... & pk_n^m\\\end{bmatrix}\]](https://delfr.com/wp-content/ql-cache/quicklatex.com-31628a837c53c82f2f13a4fbaba9dd36_l3.png)
and a signature given by
- Let
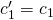
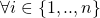 :
:
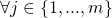 , compute:
, compute:

- The MLSAG verification algorithm
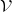 checks if
checks if 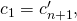 where
where

If equality holds, the signature is valid and
 outputs True. Otherwise, it outputs False.
outputs True. Otherwise, it outputs False.  is a deterministic algorithm.
is a deterministic algorithm.
- Let
- The ring linkability algorithm
 . It takes a
. It takes a  -verified valid signature
-verified valid signature  . It checks if any component of the key-image vector
. It checks if any component of the key-image vector 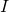 was used in the past by comparing it to previous key-image vector components stored in a set
was used in the past by comparing it to previous key-image vector components stored in a set 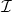 . If a match is found, then with overwhelming probability the 2 signatures were produced by the same key-pair vector (as will be justified when we prove the exculpability of the MLSAG scheme in section 5 below), and
. If a match is found, then with overwhelming probability the 2 signatures were produced by the same key-pair vector (as will be justified when we prove the exculpability of the MLSAG scheme in section 5 below), and  outputs Linked. Otherwise, its key-image vector is added to
outputs Linked. Otherwise, its key-image vector is added to 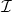 and
and  outputs Independent.
outputs Independent.
3. Security analysis – Correctness
Let ![]() be an MLSAG
be an MLSAG ![]() -generated signature. Without loss of generality, assume
-generated signature. Without loss of generality, assume ![]() . Then
. Then ![]() , we have the following implication:
, we have the following implication:
If ![]() then:
then:
-

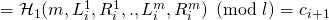
and
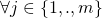 :
: -
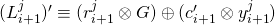
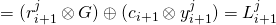
-
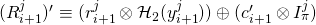
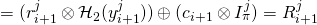
Recall that ![]() (by design of
(by design of ![]() ) and so
) and so ![]() and
and ![]() . We therefore conclude by induction on
. We therefore conclude by induction on ![]() that
that ![]() ,
, ![]() . In particular,
. In particular, ![]() . This implies that
. This implies that ![]() :
:
We can then invoke a similar induction argument on ![]() as the one stated earlier, but this time for
as the one stated earlier, but this time for ![]() . We therefore conclude that:
. We therefore conclude that:
![]() (by design of
(by design of ![]() )
)
![]()
(by induction proof showing that ![]() and
and ![]() )
)
![]()
Subsequently, any MLSAG ![]() -generated signature will satisfy
-generated signature will satisfy ![]() ‘s verification test.
‘s verification test.
4. Security analysis – Unforgeability vis-a-vis EFACM
To demonstrate that the MLSAG scheme is unforgeable, we follow the 5-step approach outlined earlier in part 1. (Recall that for ring signatures, we prove resilience against EFACM with respect to a fixed ring attack as described in part 3 of this series. The nuance here is that we have a fixed public key matrix ![]() , as opposed to a fixed public key vector
, as opposed to a fixed public key vector ![]() ).
).
Step 1: To prove that this scheme is secure against EFACM in the RO model, we proceed by contradiction and assume that there exists a PPT adversary ![]() such that:
such that:
![]()
for ![]() non-negligible in
non-negligible in ![]()
Step 2: Next, we build a simulator ![]() such that it:
such that it:
- Does not have access to any component of the private key vector of any signer.
- Has the same range as the original signing algorithm
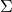 (i.e., they output MLSAG signatures taken from the same pool of potential MLSAG signatures over all possible choices of RO functions and random tapes
(i.e., they output MLSAG signatures taken from the same pool of potential MLSAG signatures over all possible choices of RO functions and random tapes 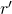 and
and  ).
). - Has indistinguishable probability distribution from that of
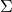 over this range.
over this range.

The reason we introduced ![]() as opposed to introducing only
as opposed to introducing only ![]() is that the simulator makes use of the random elements
is that the simulator makes use of the random elements ![]() in order to set
in order to set ![]() to the desired value. In other words, in the absence of knowledge about
to the desired value. In other words, in the absence of knowledge about ![]() , the simulator needs to have access to the random element
, the simulator needs to have access to the random element ![]() that is used in the calculation of
that is used in the calculation of ![]() in order to ensure that
in order to ensure that ![]() equates to
equates to ![]()
By construction, the output of ![]() will satisfy the verification equation. Moreover, it does its own random assignments to what otherwise would be calls to RO
will satisfy the verification equation. Moreover, it does its own random assignments to what otherwise would be calls to RO ![]() (i.e.,
(i.e., ![]() bypasses RO
bypasses RO ![]() ). Next, note the following:
). Next, note the following:
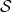 does not use any private key.
does not use any private key.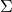 and
and 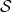 both have a range
both have a range

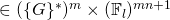
such that
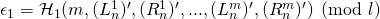 and where
and where 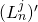 and
and 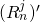 are calculated as follows:
are calculated as follows:- Let
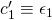
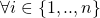 :
:
 compute:
compute:
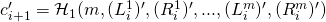
- Let
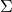 and
and 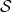 have the same probability distribution over
have the same probability distribution over 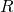 . Indeed,
. Indeed,  , we have:
, we have:
- For

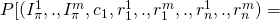
![Rendered by QuickLaTeX.com (\gamma^1,.,\gamma^m, \epsilon_{1},\beta_{1}^1,.,\beta_{1}^m,.,\beta_{n}^1,.,\beta_{n}^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-31fb925a93c9115aa1df10513fc01f1f_l3.png)
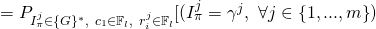
![Rendered by QuickLaTeX.com \cap\ (c_1 = \epsilon_1)\ \cap\ (r_i^j = \beta_i^j,\ \forall i \in \{{1,...,n\}},\ j \in \{{1,...,m\}})]](https://delfr.com/wp-content/ql-cache/quicklatex.com-ac7b44969b2fd20a8751ddcffc26a9a1_l3.png)
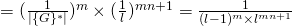
The first factor is the probability of choosing the exact
 value in the set
value in the set 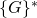 that is equal to
that is equal to 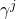 . The second factor is the probability of choosing the exact
. The second factor is the probability of choosing the exact 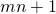 values given by
values given by 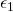 and the
and the 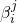 ‘s
‘s 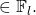
- For
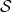 :
:
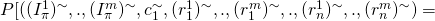
![Rendered by QuickLaTeX.com (\gamma^1,.,\gamma^m, \epsilon_{1},\beta_{1}^1,.,\beta_{1}^m,.,\beta_{n}^1,.,\beta_{n}^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-31fb925a93c9115aa1df10513fc01f1f_l3.png)
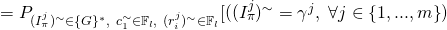
![Rendered by QuickLaTeX.com \cap\ (c_1^{\sim} = \epsilon_1)\ \cap\ ((r_i^j)^{\sim} = \beta_i^j,\ \forall i \in \{{1,...,n\}},\ j \in \{{1,...,m\}})]](https://delfr.com/wp-content/ql-cache/quicklatex.com-16c09d6eaf4b7b24fa1e2e74a4f25cae_l3.png)
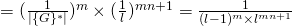
Note that the range of
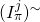 is equal to
is equal to 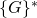 by construction of
by construction of  . And so the first factor is the probability of choosing the exact
. And so the first factor is the probability of choosing the exact 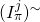 value in the set
value in the set 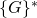 that is equal to
that is equal to 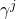 . The second factor is the probability of choosing the exact
. The second factor is the probability of choosing the exact 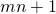 values given by
values given by 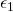 and the
and the 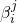 ‘s
‘s 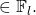
- For
With ![]() adequately built, we conclude that (as justified in section 6 of part 1):
adequately built, we conclude that (as justified in section 6 of part 1):
![]()
for ![]() non-negligible in
non-negligible in ![]() .
.
Step 3: We now show that for the MLSAG scheme, the probability of faulty collisions is negligible (refer to section 6 of part 1 for an overview). The 2 tyes of collisions are:
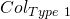 :
: 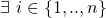 such that a tuple
such that a tuple 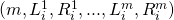 that
that 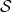 encounters — recall that
encounters — recall that 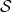 makes its own random assignment to
makes its own random assignment to 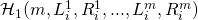 and bypasses RO
and bypasses RO 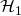 — also appears in the list of queries that
— also appears in the list of queries that 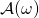 sends to RO
sends to RO  . A conflict in the 2 values will happen with overwhelming probability and the execution will halt.
. A conflict in the 2 values will happen with overwhelming probability and the execution will halt.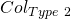 :
:  such that a tuple
such that a tuple 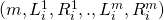 that
that 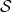 encounters —
encounters — 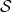 makes its own random assignment to
makes its own random assignment to  — is similar to
— is similar to 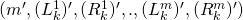 that
that 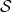 encountered earlier — here too,
encountered earlier — here too, 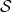 randomly assigns
randomly assigns 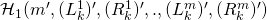 . Since
. Since
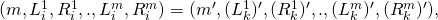
the assignments must also match, i.e.,
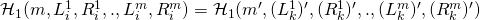
However, the likelihood that the 2 are equal is negligible. Hence they will be different with overwhelming probability and the execution will halt.
The aforementioned collisions must be avoided. In order to do so, we first calculate the probability of their occurrence in an MLSAG scheme. We assume that during an EFACM attack, ![]() can make a maximum of
can make a maximum of ![]() queries to RO
queries to RO ![]() , a maximum of
, a maximum of ![]() queries to RO
queries to RO ![]() , and a maximum of
, and a maximum of ![]() queries to
queries to ![]() .
. ![]() ,
, ![]() , and
, and ![]() are all assumed to be polynomial in the security parameter
are all assumed to be polynomial in the security parameter ![]() , since the adversary is modeled as a PPT Turing machine.
, since the adversary is modeled as a PPT Turing machine.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(since ![]() by design).
by design).
Recalling that ![]() and
and ![]() are polynomial in
are polynomial in ![]() , we conclude that
, we conclude that ![]() is negligible in
is negligible in ![]()
Next, we compute ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(since ![]() by design).
by design).
Recalling that ![]() is polynomial in
is polynomial in ![]() , we conclude that
, we conclude that ![]() is negligible in
is negligible in ![]()
Putting it altogether, we find that the below quantity is negligible in ![]() :
:
![]()
![]()
This allows us to conclude that the below quantity is non-negligible in ![]() (refer to section 6 of part 1 for a justification):
(refer to section 6 of part 1 for a justification):
![]()
Step 4: In this step, our objective is to show that if ![]() is a successful tuple that generated a first MLSAG EFACM forgery, then the following quantity is non-negligible in
is a successful tuple that generated a first MLSAG EFACM forgery, then the following quantity is non-negligible in ![]()
![]()
![]()
![]()
Here ![]() is an appropriate index that we will define in the proof. To further simplify the notation, we let
is an appropriate index that we will define in the proof. To further simplify the notation, we let ![]() and
and ![]() for all
for all ![]() . (
. (![]() and
and ![]() denote respectively the
denote respectively the ![]() query to
query to ![]() and to
and to ![]() ).
).
Let’s take a closer look at
![]()
Any successful MLSAG forgery ![]() must satisfy the verification equation
must satisfy the verification equation ![]() where we let
where we let ![]() , and
, and ![]()
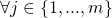 , compute:
, compute:
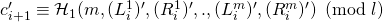
We distinguish between 3 scenarios (without loss of generality, we assume that all ![]() -queries sent to RO
-queries sent to RO ![]() are distinct from each-other. Similarly, all
are distinct from each-other. Similarly, all ![]() -queries sent to RO
-queries sent to RO ![]() are distinct from each-other. This is because we can assume that
are distinct from each-other. This is because we can assume that ![]() keeps a local copy of previous query results and avoid redundant calls):
keeps a local copy of previous query results and avoid redundant calls):
- Scenario 1:
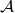 was successful in its forgery, and
was successful in its forgery, and
- No collisions occured, and
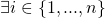 such that it never queried RO
such that it never queried RO 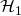 on input
on input 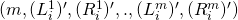 .
.
- Scenario 2:
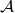 was successful in its forgery, and
was successful in its forgery, and
- No collisions occured, and
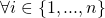 it queried RO
it queried RO 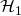 on input
on input 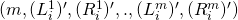 during execution, and
during execution, and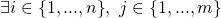 such that it queried RO
such that it queried RO 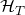 on input
on input 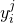 after it had queried RO
after it had queried RO 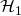 on input
on input 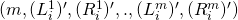 .
.
- Scenario 3:
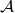 was successful in its forgery, and
was successful in its forgery, and
- No collisions occured, and
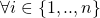 it queried RO
it queried RO 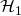 on input
on input 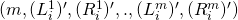 during execution, and
during execution, and , it queried RO
, it queried RO 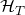 on input
on input 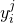 before it queried RO
before it queried RO 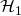 on input
on input 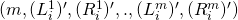
The probability of scenario 1 is upper-bounded by the probability that ![]() picks
picks ![]() such that it matches the value of
such that it matches the value of ![]() . If the 2 values don’t match, then
. If the 2 values don’t match, then ![]() will be different than
will be different than ![]() (by the verification algorithm
(by the verification algorithm ![]() ). It is upper-bounded because at the very least, this constraint must be observed to pass the verification test.
). It is upper-bounded because at the very least, this constraint must be observed to pass the verification test. ![]() is the value that RO
is the value that RO ![]() returns to
returns to ![]() (the verification algorithm) when verifying the validity of the forged signature. And since
(the verification algorithm) when verifying the validity of the forged signature. And since ![]() can be any value in the range of
can be any value in the range of ![]() (which was defined to be
(which was defined to be ![]() ) we get:
) we get:
![]() , which is negligible in
, which is negligible in ![]()
In scenario 2, let ![]() and
and ![]() be 2 indices such that
be 2 indices such that ![]() queried RO
queried RO ![]() on input
on input ![]() after it had queried RO
after it had queried RO ![]() on input
on input ![]() . Note that during the verification process,
. Note that during the verification process, ![]() will calculate
will calculate ![]() and hence will make a call to
and hence will make a call to ![]() on input
on input ![]() (remember that
(remember that ![]() is derived from
is derived from ![]() ). The probability that the resulting
). The probability that the resulting ![]() matches the
matches the ![]() argument previously fed to
argument previously fed to ![]() is upper-bounded by
is upper-bounded by ![]() (since the range of
(since the range of ![]() ). Moreover,
). Moreover, ![]() can be any index in
can be any index in ![]() and
and ![]() any index in
any index in ![]() . We get:
. We get:
![]() , which is negligible in
, which is negligible in ![]()
So we assume that a successful MLSAG forgery will likely be of the Scenario 3 type.
![]()
![]()
![]()
which is non-negligible in ![]()
The rest of the proof for Step 4 is exactly the same as the one outlined for the LSAG scheme. We will not reproduce it here (the reader can refer to the details in section 4 of part 5).
Step 5: The final step uses the 2 forgeries obtained earlier to solve an instance of the Discrete Logarithm (DL) problem. Here is a recap of Step 4 results:
- With non-negligible probability of at least
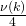 we get a successful tuple
we get a successful tuple 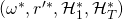 , s.t.
, s.t.  for some vector of indices
for some vector of indices 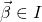 (note that in this context,
(note that in this context, 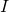 refers to a specific set of indices and not to the key-image vector. Review section 4 of part 5 for a definition of
refers to a specific set of indices and not to the key-image vector. Review section 4 of part 5 for a definition of 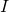 and
and  ). By running
). By running 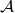 a number of times polynomial in
a number of times polynomial in 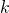 , we can find such a tuple.
, we can find such a tuple. - Once we find such a tuple, we’ve also shown that with non-negligible probability of at least
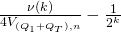 , we can find another successful tuple
, we can find another successful tuple 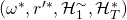 s.t.
s.t. 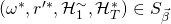 and
and 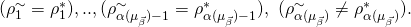
Let ![]() correspond to forgery
correspond to forgery
![]()
and ![]() correspond to forgery
correspond to forgery
![]()
Recall that ![]() is the index of the last query of the form
is the index of the last query of the form
![]()
that ![]() sends to RO
sends to RO ![]() (
(![]() ). Since the 2 experiments corresponding to the 2 successful tuples have:
). Since the 2 experiments corresponding to the 2 successful tuples have:
- The same random tapes
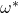 and
and 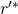
- The same RO
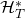
- ROs
 and
and  behave the same way on the first
behave the same way on the first 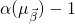 queries,
queries,
we can be confident that the first ![]() queries sent to the 2 ROs
queries sent to the 2 ROs ![]() and
and ![]() are identical. In other words, we have
are identical. In other words, we have ![]()
![]()
Without loss of generality, let ![]() , (where
, (where ![]() ), correspond to the last query of this type sent to RO
), correspond to the last query of this type sent to RO ![]() . That means that
. That means that ![]() is the
is the ![]() query sent to RO
query sent to RO ![]() . We have:
. We have:
![]()
![]()
(where (![]() whenever
whenever ![]() )
)
![]()
![]()
![]()
(by writing ![]()
Moreover, we have
![]()
(by definition of ![]() in
in ![]() )
)
![]()
(by design of the forgery tuples)
![]()
(by definition of ![]() in
in ![]() )
)
And so ![]() , we can solve for
, we can solve for ![]() in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that MLSAG is secure against EFACM in the RO model.
in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that MLSAG is secure against EFACM in the RO model.
5. Security analysis – Exculpability
This section is concerned with the notion of exculpability from an unforgeability standpoint as described in [1]. A detailed discussion can be found in part 5 of this series. The setting is similar to the one previously described in part 5 and part 6, with a small nuance. Suppose all ![]() private keys of each member of an
private keys of each member of an ![]() subset of ring members have been compromised in an
subset of ring members have been compromised in an ![]() -ring setting. Let
-ring setting. Let ![]() denote the index of the only non-compromised user with key-vector
denote the index of the only non-compromised user with key-vector ![]() , and let
, and let ![]() denote the key-image vector associated with it. We investigate whether it is likely to produce a valid forgery with key-image vector that includes at least one component equal to
denote the key-image vector associated with it. We investigate whether it is likely to produce a valid forgery with key-image vector that includes at least one component equal to ![]() for some
for some ![]() . In what follows, we show that this can only happen with negligible probability. In essence, this means that a non-compromised honest ring member (by honest we mean a ring member that signs at most once using his private key-vector) does not run the risk of encountering a forged signature that carries any component of his key-image vector. In the context of Monero, this implies that a non-compromised honest ring member cannot be accused of signing twice using the same key-image vector, and hence is exculpable.
. In what follows, we show that this can only happen with negligible probability. In essence, this means that a non-compromised honest ring member (by honest we mean a ring member that signs at most once using his private key-vector) does not run the risk of encountering a forged signature that carries any component of his key-image vector. In the context of Monero, this implies that a non-compromised honest ring member cannot be accused of signing twice using the same key-image vector, and hence is exculpable.
Note that since the adversary ![]() has access to all the compromised private keys of
has access to all the compromised private keys of ![]() members, it can easily calculate their corresponding public key vectors. Doing so will allow it to identify the public key vector
members, it can easily calculate their corresponding public key vectors. Doing so will allow it to identify the public key vector ![]() of the non-compromised ring member and hence determine the index
of the non-compromised ring member and hence determine the index ![]() . In order to prove the exculpability of the MLSAG scheme, we follow an almost identical proof to that of the previous section (i.e., unforgeability vis-a-vis EFACM) and apply the same 5-step approach. The objective is to show that this particular type of forgery would imply the ability to solve the DL of at least one component of
. In order to prove the exculpability of the MLSAG scheme, we follow an almost identical proof to that of the previous section (i.e., unforgeability vis-a-vis EFACM) and apply the same 5-step approach. The objective is to show that this particular type of forgery would imply the ability to solve the DL of at least one component of ![]() . The nuance resides in the specific index
. The nuance resides in the specific index ![]() for which the DL will be solved, as opposed to any other index. This is because we assume that all the other members are compromised and hence their DLs (i.e., private keys) are common-knowledge.
for which the DL will be solved, as opposed to any other index. This is because we assume that all the other members are compromised and hence their DLs (i.e., private keys) are common-knowledge.
Step 1: We proceed by contradiction and assume that there exists a PPT adversary ![]() such that:
such that:
![]()
![]() , for
, for ![]() non-negligible in
non-negligible in ![]()
We refer to “succeeds in creating a forgery ![]() as
as ![]() . We re-write the above equation as:
. We re-write the above equation as:
![]()
![]() , for
, for ![]() non-negligible in
non-negligible in ![]()
The notation used makes it explicit that ![]() can access the set of compromised key vectors
can access the set of compromised key vectors ![]() with
with ![]() excluded. Success is defined as issuing a forged signature with a key image vector that shares at least one component with the key image vector of the non-compromised user
excluded. Success is defined as issuing a forged signature with a key image vector that shares at least one component with the key image vector of the non-compromised user ![]() . We let this component be
. We let this component be ![]() for some
for some ![]() . (Recall that
. (Recall that ![]() is derived from
is derived from ![]()
Step 2: The next step consists in building a simulator ![]() such that it:
such that it:
- Does not have access to any component of the private key vector of any signer.
- Has the same range as the original signing algorithm
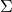 (i.e., they output MLSAG signatures taken from the same pool of potential MLSAG signatures over all possible choices of RO functions and respective random tapes
(i.e., they output MLSAG signatures taken from the same pool of potential MLSAG signatures over all possible choices of RO functions and respective random tapes 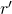 and
and  ).
). - Has indistinguishable probability distribution from that of
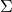 over this range.
over this range.
The simulator ![]() is the same as the one we built in the previous section. The only difference is that
is the same as the one we built in the previous section. The only difference is that ![]() does not choose a random index
does not choose a random index ![]() , since
, since ![]() already knows the index of the non-compromised ring member.
already knows the index of the non-compromised ring member.
Step 3: The logical reasoning and procedure are identical to those of the previous section. We conclude that
![]()
![]()
Step 4: Here too, the logical reasoning and procedure are identical to those of the previous section. In particular, we define the following sets in a similar way:
and conclude that:
![]()
![]()
![]() , which is non-negligible in
, which is non-negligible in ![]()
Here ![]() , as before, is an appropriately defined index,
, as before, is an appropriately defined index, ![]()
![]() for all
for all ![]() and
and ![]() denotes the
denotes the ![]() query sent to RO.
query sent to RO.
Step 5: The final step uses the 2 forgeries obtained earlier to solve an instance of the Discrete Logarithm (DL) problem. Here is a recap of Step 4 results:
- With non-negligible probability of at least
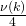 we get a successful tuple
we get a successful tuple 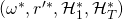 , s.t.
, s.t.  for some vector of indices
for some vector of indices 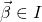 (note that in this context,
(note that in this context, 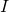 refers to a specific set of indices and not to the key-image vector. Review section 4 of part 5 for a definition of
refers to a specific set of indices and not to the key-image vector. Review section 4 of part 5 for a definition of 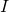 and
and  ). By running
). By running 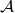 a number of times polynomial in
a number of times polynomial in 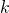 , we can find such a tuple.
, we can find such a tuple. - Once we find such a tuple, we’ve also shown that with non-negligible probability of at least
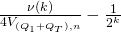 , we can find another successful tuple
, we can find another successful tuple 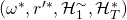 s.t.
s.t. 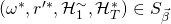 and
and 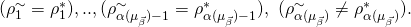
Let ![]() correspond to forgery
correspond to forgery
![]()
and ![]() correspond to forgery
correspond to forgery
![]()
Recall that ![]() is the component of
is the component of ![]() ‘s key image vector that appears in the forgery.
‘s key image vector that appears in the forgery. ![]() is the index of the last query that
is the index of the last query that ![]() sends to RO
sends to RO ![]() of the form
of the form ![]() Since the 2 experiments corresponding to the 2 successful tuples have:
Since the 2 experiments corresponding to the 2 successful tuples have:
- The same random tapes
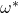 and
and 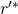
- The same RO
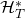
- ROs
 and
and  behave the same way on the first
behave the same way on the first 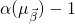 queries,
queries,
we can be confident that the first ![]() queries sent to the 2 ROs
queries sent to the 2 ROs ![]() and
and ![]() are identical. In other words, we have
are identical. In other words, we have ![]()
![]()
![]()
![]() , and
, and ![]()
In particular, for the index ![]() that corresponds to the component
that corresponds to the component ![]() that appears in the forgery, we let
that appears in the forgery, we let ![]() , and
, and ![]() . For each
. For each ![]() , we get 2 identical systems of
, we get 2 identical systems of ![]() equations dictated by
equations dictated by ![]() ‘s verification computation:
‘s verification computation:

![]() , the first system is a linear system of 2 equations in variables
, the first system is a linear system of 2 equations in variables ![]() and
and ![]() . Similarly, the second system is a linear system of 2 equations in variables
. Similarly, the second system is a linear system of 2 equations in variables ![]() and
and ![]() . The 2 systems are identical with different variable names. Hence, if
. The 2 systems are identical with different variable names. Hence, if ![]() is a unique solution to the first system and
is a unique solution to the first system and ![]() a unique solution to the second, we can be confident that
a unique solution to the second, we can be confident that ![]() and
and ![]() . (Note that for any index
. (Note that for any index ![]() other than
other than ![]() , the 2 forged signatures do not necessarily share the same image-key component. In other terms
, the 2 forged signatures do not necessarily share the same image-key component. In other terms ![]() is not necessarily equal
is not necessarily equal ![]() and so the 2 systems of linear equations would be different from each other). For either system to admit a unique solution, the 2 equations must be linearly independent. We re-write the 2 systems as follows:
and so the 2 systems of linear equations would be different from each other). For either system to admit a unique solution, the 2 equations must be linearly independent. We re-write the 2 systems as follows:

If we multiply the second equation by ![]() (multiplication refers to
(multiplication refers to ![]() ), we see that a sufficient condition for the system to be linearly independent is to have
), we see that a sufficient condition for the system to be linearly independent is to have ![]() . Next, we show that with overwhelming probability, the system is indeed independent
. Next, we show that with overwhelming probability, the system is indeed independent ![]() :
:
- Recall that the range of
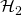 is
is 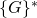 and that the order of
and that the order of 
- Therefore,
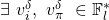 such that
such that 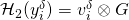 and
and 
- We can then re-write the sufficient condition as
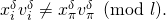
- Note that given
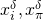 , and
, and 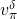 , there is at most one value of
, there is at most one value of 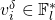 that satisfies
that satisfies 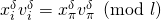 . Otherwise, we would have
. Otherwise, we would have
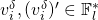 ,
, 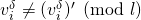 , and
, and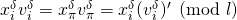
This would imply that
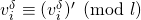 , a contradiction.
, a contradiction. - Noting that each
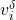 corresponds to a distinct
corresponds to a distinct 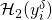 , we conclude that given
, we conclude that given 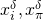 and
and 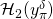 there is at most one
there is at most one 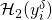 s.t.
s.t. ![Rendered by QuickLaTeX.com [x_i^{\delta} \otimes \mathcal{H}_2(y_i^{\delta})]\ =\ I_{\pi}^{\delta} \equiv [x_{\pi}^{\delta} \otimes \mathcal{H}_2(y_{\pi}^{\delta})].](https://delfr.com/wp-content/ql-cache/quicklatex.com-20e1adb0b7f69e0232e93c111e11dd39_l3.png)
- Since
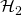 is a RO outputing random values, the probability of getting the right value of
is a RO outputing random values, the probability of getting the right value of 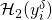 is
is 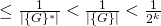 (negligible in
(negligible in 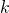 ).
).
![]() , we therefore conclude that with overwhelming probability we have
, we therefore conclude that with overwhelming probability we have ![]() . We can then be confident that the linear system of 2 equations has a unique solution. Hence,
. We can then be confident that the linear system of 2 equations has a unique solution. Hence, ![]() , we have
, we have ![]() , and
, and ![]()
Moreover, by design of the 2 forgeries, we know that there exists one and only one ![]() (corresponding to the
(corresponding to the ![]() query sent to RO
query sent to RO ![]() ) that satisfies
) that satisfies
![]()
(by definition of ![]() in
in ![]() )
)
![]()
(by design of the forgery tuples)
![]()
(by definition of ![]() in
in ![]() )
)
But ![]() , we showed that with overwhelming probability
, we showed that with overwhelming probability ![]() . Therefore, it must be that
. Therefore, it must be that ![]() and so
and so ![]()
Going back to the system of 2 equations associated with ![]() , we write:
, we write:
![]()
That means that we can solve for ![]() in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that the MLSAG scheme is exculpable and secure against
in polynomial time, contradicting the intractability of DL on elliptic curve groups. We conclude that the MLSAG scheme is exculpable and secure against ![]() in the RO model.
in the RO model.
6. Security analysis – Anonymity
In this section, we show that the MLSAG scheme satisfies the weaker anonymity definition #2 introduced in part 3 of this series. Note that as we previously observed in part 5, linkable signatures cannot satisfy anonymity definition #1.
More formally, let ![]() be a PPT adversary with random tape
be a PPT adversary with random tape ![]() that takes 4 inputs:
that takes 4 inputs:
- Any message
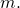
- A public key matrix
![Rendered by QuickLaTeX.com PK \equiv [\vec{y_1}\ ...\ \vec{y_n}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e519a251b89c303eb9a2e4ea4c1a2781_l3.png) that includes
that includes ![Rendered by QuickLaTeX.com \vec{y_{\pi}} \equiv [y_{\pi}^1\ ...\ y_{\pi}^m]^T](https://delfr.com/wp-content/ql-cache/quicklatex.com-0f4291cdec1f33990a3ddefd8b232d73_l3.png) of the signer.
of the signer. - A list
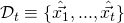 of compromised private key vectors (
of compromised private key vectors (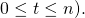
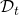 can be empty and
can be empty and 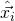 may be different than
may be different than  for
for 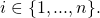 But
But 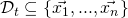
- A valid signature
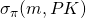 on message
on message 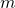 , public key matrix
, public key matrix 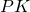 and actual signer private key vector
and actual signer private key vector ![Rendered by QuickLaTeX.com \vec{x_{\pi}} \equiv [x_{\pi}^1\ ...\ x_{\pi}^m]^T.](https://delfr.com/wp-content/ql-cache/quicklatex.com-80ca06cd15d802c55c43637b3af449fe_l3.png)
![]() outputs an index in
outputs an index in ![]() that it thinks is that of the actual signer. Definition # 2 mandates that for any polynomial
that it thinks is that of the actual signer. Definition # 2 mandates that for any polynomial ![]() in security parameter
in security parameter ![]() , we have:
, we have:
![]()
![]()
if ![]() and
and ![]()
![]()
![]()
if ![]() or
or ![]()
In the RO model, ![]() can send a number of queries (polynomial in
can send a number of queries (polynomial in ![]() ) to RO
) to RO ![]() and RO
and RO ![]() . The probability of
. The probability of ![]() ‘s success is computed over the distributions of
‘s success is computed over the distributions of ![]() and
and ![]() . Making explicit the dependence on the ROs, definition # 2’s condition becomes:
. Making explicit the dependence on the ROs, definition # 2’s condition becomes:
![]()
![]()
if ![]() and
and ![]()
![]()
![]()
if ![]() or
or ![]()
In order to prove that anonymity holds in the above sense, we proceed by contradiction and rely on the intractability of the Decisional Diffie Hellman problem or DDH for short (refer to part 5 for a discussion of DDH). We consider 3 separate cases:
Case 1: ![]() and
and ![]()
Suppose that ![]() in PPT(
in PPT(![]() ) and
) and ![]() non-negligible in
non-negligible in ![]() such that
such that
![]()
![]()
if ![]() and
and ![]()
Recall that since ![]() , one can automatically rule out all the compromised ring members as possible signers (the logic is similar to what was described in the anonymity section of part 5). One can then limit the guessing range of the identity of the signer to the uncompromised batch of
, one can automatically rule out all the compromised ring members as possible signers (the logic is similar to what was described in the anonymity section of part 5). One can then limit the guessing range of the identity of the signer to the uncompromised batch of ![]() remaining members.
remaining members.
We now build ![]() PPT(
PPT(![]() ) that colludes with
) that colludes with ![]() to solve the DDH problem. The input to
to solve the DDH problem. The input to ![]() consists of 1) The tuple
consists of 1) The tuple ![]() being tested for DDH, 2) A certain ring size
being tested for DDH, 2) A certain ring size ![]() (randomly chosen), 3) A number
(randomly chosen), 3) A number ![]() of compromised members (randomly chosen), and 4) A message
of compromised members (randomly chosen), and 4) A message ![]() (randomly chosen).
(randomly chosen).
![]() outputs a tuple consisting of 1) The message
outputs a tuple consisting of 1) The message ![]() , 2) A randomly generated public key matrix
, 2) A randomly generated public key matrix ![]() , 3) A randomly chosen set
, 3) A randomly chosen set ![]() of
of ![]() compromised secret key vectors, and 4) A not-necessarily valid signature
compromised secret key vectors, and 4) A not-necessarily valid signature ![]() assigned to ring member
assigned to ring member ![]() s.t.
s.t. ![]() . We let
. We let ![]() do the following:
do the following:
![]() feeds its output
feeds its output ![]() to
to ![]() . In order for
. In order for ![]() to use its advantage in guessing the signer’s identity, it must be given a valid signature (i.e., a signature that is an element of the range of acceptable MLSAG signatures over all RO
to use its advantage in guessing the signer’s identity, it must be given a valid signature (i.e., a signature that is an element of the range of acceptable MLSAG signatures over all RO ![]() . For
. For ![]() to be a valid signature,
to be a valid signature, ![]() must be a DDH instance. Indeed, let
must be a DDH instance. Indeed, let ![]() be partially defined as per the design of
be partially defined as per the design of ![]() . We show that for such an
. We show that for such an ![]() , the signature obtained is an element of the range of acceptable MLSAG signatures. First note the following (all the primed quantities below are as defined in the verification algorithm
, the signature obtained is an element of the range of acceptable MLSAG signatures. First note the following (all the primed quantities below are as defined in the verification algorithm ![]() :
:
If ![]() then:
then:
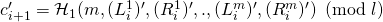
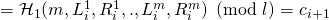
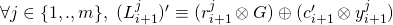
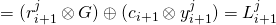

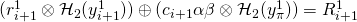 , if
, if 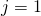
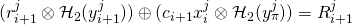 , if
, if 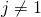
Since ![]() is a DDH instance then we necessarily have
is a DDH instance then we necessarily have ![]()
Moreover, recall that ![]() (by design of
(by design of ![]() ). And so
). And so ![]()
![]() and
and ![]() We therefore conclude by induction on
We therefore conclude by induction on ![]() that
that ![]() ,
, ![]() . In particular,
. In particular, ![]() This in turn implies that
This in turn implies that ![]() is a valid signature.
is a valid signature.
On the other hand, if ![]() is not a DDH instance, then
is not a DDH instance, then ![]() and with overwhelming probability
and with overwhelming probability ![]() is not a valid signature.
is not a valid signature.
Recall that ![]() can send queries to
can send queries to ![]() and
and ![]() during execution. It is important to enforce consistency between
during execution. It is important to enforce consistency between ![]() and
and ![]() ‘s query results obtained from RO
‘s query results obtained from RO ![]() and RO
and RO ![]() on the same input. There are no risks of faulty collisions in so far as
on the same input. There are no risks of faulty collisions in so far as ![]() is concerned (by design of
is concerned (by design of ![]() ). However,
). However, ![]() bypasses RO
bypasses RO ![]() and conducts its own backpatching to
and conducts its own backpatching to ![]() . If
. If ![]() such that
such that ![]() queries
queries ![]() on input
on input ![]() , then with overwhelming probability, it will conflict with
, then with overwhelming probability, it will conflict with ![]() ‘s backpatched value causing the execution to halt. The aforementioned collision must be avoided. In order to do so, we first calculate the probability of its occurence. We assume that during execution,
‘s backpatched value causing the execution to halt. The aforementioned collision must be avoided. In order to do so, we first calculate the probability of its occurence. We assume that during execution, ![]() can make a maximum of
can make a maximum of ![]() queries to RO
queries to RO ![]() .
. ![]() is assumed to be polynomial in the security parameter
is assumed to be polynomial in the security parameter ![]() , since the adversary is modeled as a PPT Turing machine.
, since the adversary is modeled as a PPT Turing machine.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
and so we conclude that:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Here, ![]() non-negligibale in
non-negligibale in ![]()
After execution, ![]() returns to
returns to ![]() an integer
an integer ![]() .
. ![]() outputs 1 if
outputs 1 if ![]() or outputs 0/1 with equal probability otherwise:
or outputs 0/1 with equal probability otherwise:
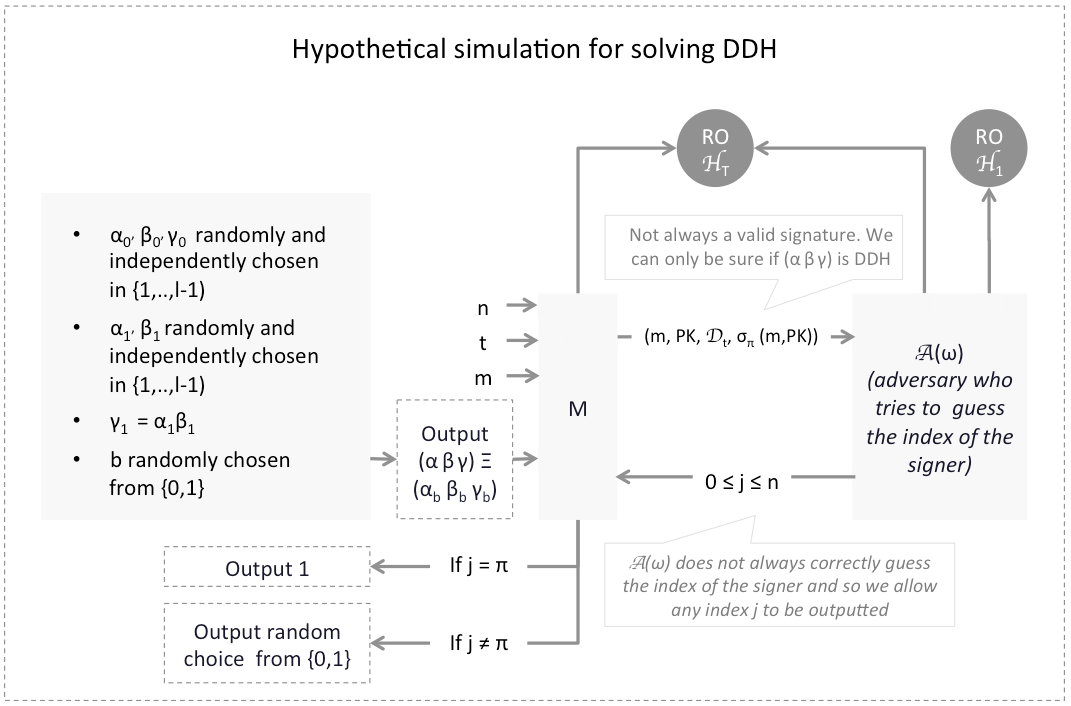
Using the setting described above, one can now calculate the probability of ![]() guessing whether
guessing whether ![]() is DDH or not. The calculation is the same as the one previously conducted in section 6 of part 5 and part 6 and leads us to conclude:
is DDH or not. The calculation is the same as the one previously conducted in section 6 of part 5 and part 6 and leads us to conclude:
![]()
Since ![]() is non-negligible in
is non-negligible in ![]() , the above probability outperforms random guessing. This contradicts the intractability of DDH. Similarly, we can show that
, the above probability outperforms random guessing. This contradicts the intractability of DDH. Similarly, we can show that
![]()
is also bounded from below. We finally conclude that for any polynomial ![]() :
:
![]()
![]()
Case 2: ![]() and
and ![]()
In this case, ![]() can check if the key-image vector
can check if the key-image vector ![]() appearing in
appearing in ![]() matches the key-image vector of any of the compromised users (i.e.,
matches the key-image vector of any of the compromised users (i.e., ![]() , for
, for ![]() . With overwhelming probability, none of them will match since we proved that the scheme is exculpable and so no one can forge a signature with a tag of a non-compromised member. Proceeding by elimination,
. With overwhelming probability, none of them will match since we proved that the scheme is exculpable and so no one can forge a signature with a tag of a non-compromised member. Proceeding by elimination, ![]() can then conclude that the signer is
can then conclude that the signer is ![]()
Case 3: ![]()
In this case, ![]() can check which of the compromised key-image vectors (i.e.,
can check which of the compromised key-image vectors (i.e., ![]() , for
, for ![]() matches the key-image vector appearing in
matches the key-image vector appearing in ![]() ). Only one of them will match (due to exculpability), subsequently revealing the identity of the signer
). Only one of them will match (due to exculpability), subsequently revealing the identity of the signer
7. Security analysis – Linkability
The linkability property means that if a secret key of a given secret key vector is used in more than one signature, then the resulting signatures will be linked and flagged by ![]() (the linkability algorithm).
(the linkability algorithm).
We proved in part 5 of this series that a signature scheme is linkable if and only if ![]() a ring of
a ring of ![]() members, it is not possible to produce
members, it is not possible to produce ![]() valid signatures with pairwise different key-images such that all of them get labeled independent by
valid signatures with pairwise different key-images such that all of them get labeled independent by ![]() . This result can be easily adapted to the case of a public key matrix
. This result can be easily adapted to the case of a public key matrix ![]() (where
(where ![]() ) and secret key vectors
) and secret key vectors ![]()
A signature scheme is linkable
![]() a ring of
a ring of ![]() members, it is not possible to produce
members, it is not possible to produce ![]() valid signatures such that no 2 key image vectors share a component in common.
valid signatures such that no 2 key image vectors share a component in common.
The proof of the above equivalence is identical to the one previously outlined in section 7 of part 5. To prove that the MLSAG scheme is linkable we follow a reductio ad absurdum approach, similar to the one described in part 5:
-
- Assume that the MLSAG signature scheme is not linkable.
- The equivalence above would imply that
![Rendered by QuickLaTeX.com \exists PK \equiv [\vec{y_1} ... \vec{y_n}]](https://delfr.com/wp-content/ql-cache/quicklatex.com-e81d020c0c12181b262281b1d09d2f96_l3.png) such that it can produce
such that it can produce 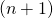 valid signatures such that no 2 key image vectors share a component in common. This means that
valid signatures such that no 2 key image vectors share a component in common. This means that
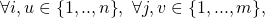
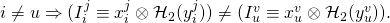
- This implies that there must exist a signature (from the set of
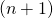 valid signatures) with key-image vector
valid signatures) with key-image vector ![Rendered by QuickLaTeX.com \vec{I_{\delta}} \equiv [I_{\delta}^1\ ...\ I_{\delta}^m]^T](https://delfr.com/wp-content/ql-cache/quicklatex.com-523973668306cccf45e966854b77e9dc_l3.png) for which
for which 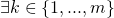 such that
such that
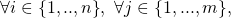
![Rendered by QuickLaTeX.com I_{\delta}^k \neq [I_i^j \equiv x_i^j \otimes \mathcal{H}_2(y_i^j)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-7ea1c1012780436f2d0d4ca353ef9913_l3.png)
Denote this signature by
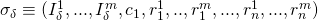
- When verifying the validity of
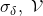 first computes the following:
first computes the following:
- Let
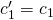
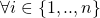 :
:
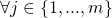 , compute:
, compute:

- Let
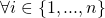 , and for
, and for 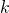 as identified above, the system of 2 equations given by
as identified above, the system of 2 equations given by 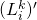 and
and 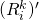 can be equivalently written as:
can be equivalently written as:
For a given
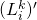 ,
, 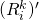 , and
, and 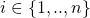 , this constitutes a system of 2 equations in variables
, this constitutes a system of 2 equations in variables  and
and 
-
-
Since
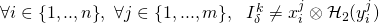 , the system of 2 equations corresponding to each
, the system of 2 equations corresponding to each 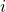 is independent and admits a unique solution
is independent and admits a unique solution 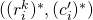 for any given
for any given 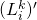 and
and 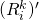 . In particular, that means that the value
. In particular, that means that the value  is well defined and equal to
is well defined and equal to 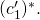
-
By virtue of being a valid signature,
 must satisfy
must satisfy  ‘s verification equation requiring that
‘s verification equation requiring that
But RO
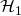 is random by definition. The probability that it outputs a specific value is eqal to
is random by definition. The probability that it outputs a specific value is eqal to  (recall that the range of
(recall that the range of 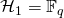 ). Since by design we have
). Since by design we have 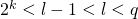 , we conclude that the probability that
, we conclude that the probability that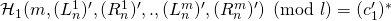
is upper-bounded by
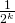 and is hence negligible. In other terms, the probability that
and is hence negligible. In other terms, the probability that 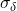 is a valid signature is negligible.
is a valid signature is negligible.
We hence conclude that the MLSAG scheme is linkable.
References
[1] E. Fujisaki and K. Suzuki. Traceable ring signatures. Public Key Cryptography, pages 181-200, 2007.
[2] S. Noether and A. Mackenzie. Ring condential transactions. Monero Research Lab, 2016.
Tags: LSAG, MLSAG, Monero, multilayered, ring signature, Security

No comments
Comments feed for this article
Trackback link: https://delfr.com/mlsag-signature-moneros-part-7/trackback/