1. Introduction and Bitcoin’s elliptic curve review
The objective of this post is to introduce the reader to Bitcoin’s private and public keys, and to the Bitcoin addresses used in Pay to Public Key Hash transactions (P2PKH) and Pay to Script Hash transactions (P2SH).
As was previously introduced in the Elliptic Curve Groups post, the linkage between Bitcoin’s private and public keys is determined by a specific elliptic curve known as secp256k1. Recall that the curve’s parameters are as follows:
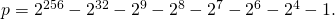 This a very large prime number that serves as the order of the underlying field
This a very large prime number that serves as the order of the underlying field 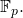
- The secp256k1 curve is non-singular and is represented using its short Weierstrass form. We denoted the resulting group by
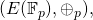 where
where
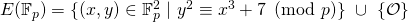
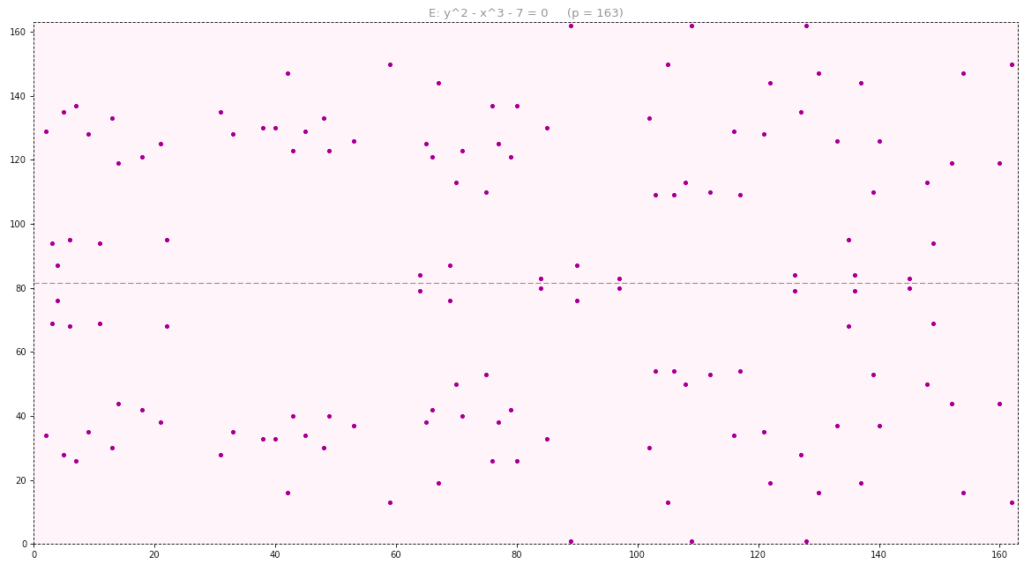
 denotes the point at infinity and is the identity element of the group. Here is a euclidean representation of this curve when
denotes the point at infinity and is the identity element of the group. Here is a euclidean representation of this curve when 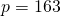 (it is not feasible to show it for
(it is not feasible to show it for 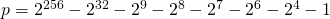 ).
).
- The base point
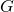 has abscissa and ordinate given by
has abscissa and ordinate given by
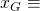
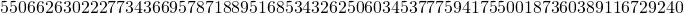
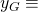
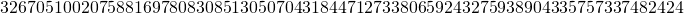
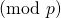
which in hexadecimal notation are given by:
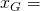 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798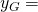 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8Bitcoin’s public-key cryptography is hence conducted on the subgroup
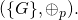
- The order of
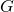 is chosen to be a prime number equal to
is chosen to be a prime number equal to
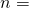
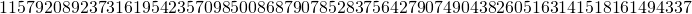
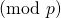
which in hexadecimal notation is given by
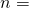 FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 - Recall that
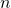 denotes the order of
denotes the order of 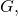 and must divide
and must divide 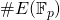 i.e., the order of
i.e., the order of 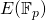 . The cofactor
. The cofactor 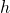 is equal to
is equal to 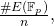 which in this case is equal to 1. That means that the order of
which in this case is equal to 1. That means that the order of 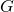 is equal to that of
is equal to that of 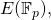 i.e.,
i.e., 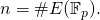 Since
Since 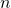 is prime, the order of
is prime, the order of 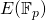 is also prime. As a result,
is also prime. As a result, 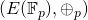 is a cyclic group and any of its elements could serve as a generator.
is a cyclic group and any of its elements could serve as a generator.
We also saw that Bitcoin’s private and public keys obey the following architecture:
- A private key
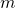 is a 256-bit long scalar chosen from the set
is a 256-bit long scalar chosen from the set
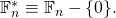
- A public key
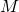 is an element of the subgroup
is an element of the subgroup 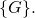
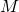 is derived from
is derived from 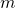 by adding
by adding 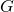 to itself a total of
to itself a total of 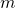 times. Addition refers to the elliptic curve group binary operation
times. Addition refers to the elliptic curve group binary operation 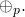 More specifically,
More specifically,
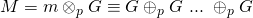 (
(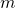 times)
times)It is a 512-bit long string denoting the elliptic curve point
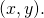 It is an element of the set
It is an element of the set 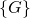 which in this case is equivalent to
which in this case is equivalent to 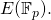 Both
Both 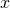 and
and 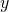 are 256-bit long.
are 256-bit long.
The most important observation was that one can efficiently calculate ![]() from
from ![]() using e.g., the double-and-add method, but that deriving
using e.g., the double-and-add method, but that deriving ![]() from
from ![]() is thought to be intractable. We saw that this conclusion is a manifestation of the exponential hardness of the Elliptic Curve Discrete Logarithm Problem (ECDLP).
is thought to be intractable. We saw that this conclusion is a manifestation of the exponential hardness of the Elliptic Curve Discrete Logarithm Problem (ECDLP).
In what follows we include four python methods, the first three of which feed into the method entitled mul_scalar that perfoms elliptic-curve point multiplication. The first two methods were sourced from [3]:
-
extended_euclidean_algorithm(a, b): it takes two integers
 and
and 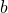 and returns a three-tuple consisting of gcd
and returns a three-tuple consisting of gcd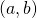 and the bezout coefficients
and the bezout coefficients 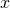 and
and 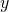 that satisfy
that satisfy 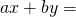 gcd
gcd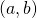 (refer to Groups and Finite Fields):
(refer to Groups and Finite Fields):def extended_euclidean_algorithm(a, b): """ Returns a three-tuple (gcd, x, y) such that a * x + b * y == gcd, where gcd is the greatest common divisor of a and b. This function implements the extended Euclidean algorithm and runs in O(log b) in the worst case. """ s, old_s = 0, 1 t, old_t = 1, 0 r, old_r = b, a while r != 0: quotient = old_r // r old_r, r = r, old_r - quotient * r old_s, s = s, old_s - quotient * s old_t, t = t, old_t - quotient * t return old_r, old_s, old_t
-
inverse_of(n,p): it computes the inverse of
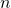 mod
mod 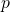 by relying on the extended_euclidean_algorithm method (refer to Groups and Finite Fields):
by relying on the extended_euclidean_algorithm method (refer to Groups and Finite Fields):def inverse_of(n, p): """ Returns the multiplicative inverse of n modulo p. This function returns an integer m such that (n * m) % p == 1. """ gcd, x, y = extended_euclidean_algorithm(n, p) assert (n * x + p * y) % p == gcd if gcd != 1: # Either n is 0, or p is not a prime number. raise ValueError( '{} has no multiplicative inverse ' 'modulo {}'.format(n, p)) else: return x % p - add_points(A, B, p, p1, p2): it adds two points
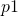 and
and 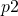 on the short Weierstrass form elliptic curve whose equation is
on the short Weierstrass form elliptic curve whose equation is
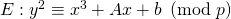
The rules for adding two points was outlined in the Elliptic Curve Groups post:
''' This method adds 2 points p1 and p2 in the elliptic curve group associated with the elliptic curve equation E: y^2 = x^3 + Ax + B mod(p) ''' def add_points(A, B, p, p1, p2): if (p1 == "O"): return p2 # "0" denotes the identity element of the group elif (p2 == "O"): return p1 else: x_p1, y_p1 = p1 x_p2, y_p2 = p2 if (not ((x_p1 - x_p2) % p) and ((y_p1 - y_p2) % p)): return "O" elif (not ((x_p1 - x_p2) % p) and (not ((y_p1 - y_p2) % p)) and (not (y_p1 % p))): return "O" elif (not ((x_p1 - x_p2) % p) and (not ((y_p1 - y_p2) % p)) and (y_p1 % p)): c = ((3*x_p1**2 + A) * inverse_of(2*y_p1, p)) % p d = (y_p1 - c*x_p1) % p x_p12 = (c**2 - 2*x_p1) % p return (x_p12, (-c*x_p12 - d) % p) elif ((x_p1 - x_p2) % p): c = ((y_p2 - y_p1) * inverse_of(x_p2 - x_p1, p)) % p d = ((x_p2 * y_p1 - x_p1 * y_p2) * inverse_of(x_p2 - x_p1, p)) % p x_p12 = (c**2 - x_p1 - x_p2) % p return (x_p12, (-c*x_p12 - d) % p)
- mul_scalar(A, B, p, p1, m): it multiplies a scalar
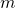 by a point
by a point 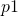 on the short Weierstrass form elliptic curve whose equation is
on the short Weierstrass form elliptic curve whose equation is
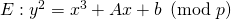
It implements the double-and-add algorithm previously introduced in the Elliptic Curve Groups post and it relies on the add_points method
def mul_scalar(A, B, p, p1, m): output = "O" while m>0: if (m&1): output = add_points(A, B, p, p1, output) m>>=1 # Shift the bit-representation of m by 1 bit to the right p1 = add_points(A, B, p, p1, p1)# and double the point p1 return output;
2. Bitcoin’s private and public keys representations
Private keys – Decimal representation: We start by generating a random private key that is 256 bits long (recall that the private key can be any number between 1 and ![]() where
where ![]() is the prime constant denoting the order of the base point
is the prime constant denoting the order of the base point ![]() ). We include below an example of a python code that does this. But first, we specify the parameters of the elliptic curve group associated with the secp256k1 curve:
). We include below an example of a python code that does this. But first, we specify the parameters of the elliptic curve group associated with the secp256k1 curve:
- p_dec denotes the decimal value of the order of the underlying finite field.
- G_dec corresponds to the decimal coordinates (mod p_dec) of the base point
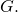
- n_dec is the decimal value of the order of
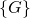 , the subgroup generated by
, the subgroup generated by 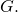
- A_dec and B_dec are the parameters of the secp256k1 curve represented in short Weierstrass form. A_dec
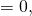 and B_dec
and B_dec 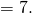
p_dec = long(2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 - 1) G_dec = (55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424) n_dec = 115792089237316195423570985008687907852837564279074904382605163141518161494337 A_dec = 0 B_dec = 7
Next, we generate a random private key in decimal notation that we assign to variable priv_key_dec
''' The private key can be any number between 1 and (n_dec - 1). In what follows, we generate a 256-bit random integer and then test if it is in the specified range. ''' priv_key_flag = False; while (priv_key_flag == False): priv_key_dec = random.getrandbits(256) # Decimal value of random 256-bit scalar priv_key_flag = 0<priv_key_dec<n_dec # Test if scalar is in the field (F_n)* print "\nThe private key in decimal representation (mod n) is: ", priv_key_dec
priv_key_dec ![]()
![]()
Private keys – Hexadecimal representation: The private key can be represented in numerous ways. All representations must however correspond to the same 256-bit number. Hexadecimal and raw binary formats are reserved for use by software and are not usually shown to end users. In python, the hex() method converts an integer to its hexadecimal representation and outputs a string of the form ‘0x….’ where the ‘0x’ prefix refers to hexadecimal format.
There is one caveat however. It is possibile for the randomly generated private key not to be big enough to fill all of the 256 bits (recall that the private key can be any positive integer less than ![]() If this is the case, we would need to add enough leading 0’s to ensure that the final length is 256 bits. The following python method is one way of completing the hexadecimal representation whenever needed:
If this is the case, we would need to add enough leading 0’s to ensure that the final length is 256 bits. The following python method is one way of completing the hexadecimal representation whenever needed:
'''
Whenever needed, this method completes the hex representation with enough leading 0's
to ensure that the total number of hexadecimal digits (i.e., nibbles) is equal to 64.
This corresponds to 32 bytes or equivalently 256 bits.
'''
def comp_256bit_hex(hex_str):# hex_str must be a hex string of the form '0x.....'
if (hex_str[-1] == "L"):# Get the hex version without "L" (long-type specifier)
hex_str = hex_str[2:-1] # Get the hex version without the'0x' prefix
else: hex_str = hex_str[2:]
l = len(hex_str)
if (l<64): return (64-l)*'0' + hex_str# add leading 0's if less than 64 nibbles
else: return hex_str# Return a hex string without the leading '0x' prefix
priv_key_hex = comp_256bit_hex(hex(priv_key_dec)) # To ensure hex format is 256-bit long print "The private key in hexadecimal format is: ", priv_key_hex
priv_key_hex ![]()
8962 D6F7 92E5 89C1 1C56 740B A30C B832 AF0A E891 A9DA 1D0C 71B4 EF9D 0043 BE2A
Private keys – WIF representation: Another format for representing private keys is the Wallet Import Format or WIF for short. The WIF format is used whenever a private key is imported or exported from one wallet to another. The Quick Response code (QR) of a private key is usually displayed in WIF format. To perform WIF encoding, the following sequential procedure (also known as the base58Check encoding procedure) is implemented:
- Insert a version prefix of ‘128′ (decimal) or ‘80′ (hexadecimal) at the beginning of the original private key.
- Perform a double sha256 on the binary representation of the newly prefixed key.
- Store the first 4 bytes (i.e., 8 nibbles) in a checksum variable.
- Append the checksum to the end of the prefixed key.
- Encoded the result in base 58.
The steps are self-explanatory, except possibly for the last one. A base 58 encoding is similar in concept to any other base transformation. The alphabet used in this case consists of the following 58 elements:
![]()
The rationale for base 58 encoding is explained in the original Bitcoin client source code:
- Its alphabet consists of all digits (except for 0) and all lower and upper case ISO basic Latin alphabet symbols (except for
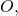
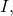 and
and 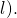 The reason for excluding them is due to the striking resemblance (when using certain fonts) of
The reason for excluding them is due to the striking resemblance (when using certain fonts) of 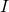 and
and 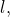 and of
and of 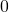 and
and 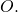 Their inclusion would possibly result in addresses and keys that visually look similar but that are actually different.
Their inclusion would possibly result in addresses and keys that visually look similar but that are actually different. - “A string with non-alphanumeric characters is not as easily accepted as an account number”. Limiting the alphabet to alphanumeric characters is safer.
- The exclusion of any punctuation character is motivated by the fact that “e-mails usually won’t line-break if there’s no punctuation to break at”.
- From a convenience standpoint, “doubleclicking selects the whole number as one word if it’s all alphanumeric”.
In what follows, we show how to convert a positive integer to its base 58 representation. Let’s take the integer 19,099 as an example:
- Divide 19,099 by 58 to obtain a quotient of 329 and a remainder of 17. Replace the remainder 17 by its corresponding alphabet symbol
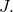
- Divide the previous quotient 329 by 58 to obtain a quotient of 5 and a remainder of 39. Replace the remainder 39 by its corresponding alphabet symbol
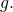
- Divide the previous quotient 5 by 58 to obtain a quotient of 0 and a remainder of 5. Replace the remainder 5 by its corresponding alphabet symbol
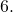
- Since the previous quotient was 0, we stop the process and conclude that the base 58 representation of 19,099 is given by
Here is an example of a python code that applies this procedure to any non-negative integer ![]()
'''
The base58 alphabet consists of 58 characters given as follows.
'''
alphabet = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz'
'''
Method to encode integers into base58 format
'''
def base58_encode_int(i): # Argument must be an integer
output = ""
while i:
i, r = divmod(i, 58)
output = alphabet[r:r+1] + output
return output
In what follows, we show how the base58Check encoding can be implemented in python. Note that it is always recommended to rely on existing implementations such as the one used by the Bitcoin client or as part of other libraries developed specifically for python. The one we include below is for educational purposes and we built it from scratch with the sole intention of illustrating the process:
- Our base58Check method takes two arguments:
- key_hex which is a hexadecimal representation of a private key, public key, or a redeem script (as we will see later when we introduce Bitcoin’s P2PKH and P2SH addresses). For WIF encoding, it represents a private key in hexadecimal representation.
- ver_prefix which holds the version prefix to be used. For WIF encoding, the version prefix is ’80’ in hex format.
- We will see shortly that the same method is used to derive the Bitcoin address associated with a given public key in the context of a P2PKH or P2SH transaction. In this case, different version prefixes will be used.
- The hashing function sha256 is applied to the binary version of the prefixed private key. To get to binary, we use python’s binascii.unhexlify(hex_str) method which acts on a hexadecimal string. There must be an even number of hex digits for it to work or an error gets raised. In our case, the even length constraint is always observed since we enforce a 256-bit long string (i.e., 64 nibbles).
''' The following method can be used to either: 1. Apply the WIF-encoding scheme to private keys (when the 'key_hex' argument is a private key in hex format, and the 'ver_prefix' argument is equal to 0x80. 2. Derive the Pay To Public Key Hash (P2PKH) bitcoin address associated with a given public key in compressed or uncompressed format (when the 'key_hex' argument is a public key in hex format, and the 'ver_prefix' argument is equal to 0x00. ''' def base58Check(key_hex, ver_prefix): # key_hex is a hex string w/o the '0x' prefix # it can be a private key (WIF encoding), a public key (P2PKH address) or a redeem sript # (P2SH address) key_hex_extended = ver_prefix + key_hex# Add the appropriate version prefix first_sha256 = sha256(binascii.unhexlify(key_hex_extended)).hexdigest() second_sha256 = sha256(binascii.unhexlify(first_sha256)).hexdigest() checksum = second_sha256[:8] # First 8 nibbles of doublesha256 output key_final = key_hex_extended + checksum# The final key in hex format ''' --- If the verion prefix is '0x00', then the encoding is being applied to a public key in order to derive the corresponding P2PKH bitcoin address. In this case, the public key is converted from hex to decimal, encoded in base 58 and then prefixed with a '1'. --- If the version prefix is '0x05', then the encoding is being applied to a script in order to derive the corresponding P2SH bitcoin address. In this case, the script is converted from hex to decimal and encoded in base 58. We don't add a leading '1'. --- If the version prefix is '0x80', then the encoding is being applied to a private key in order to convert it to its WIF format. In this case, the private key is converted from hex to decimal and encoded in base 58. We don't add a leading '1'. ''' if (ver_prefix == '00'): return '1' + base58_encode_int(int(key_final, 16)) else: return base58_encode_int(int(key_final, 16))
We can now obtain the WIF-encoded private key as follows:
priv_key_wif = base58Check(priv_key_hex, '80') print "The WIF-encoded private key is: ", priv_key_wif
priv_key_wif ![]()
5JrnvbTmxMqYNFVpcyuBq196xLsrTG7yXNCeRRi1DeDibFZFEoA
A private key encoded in WIF format will always start with a 5. To see why, note that the base58Check method creates a 37-byte long string (a byte-long version prefix, a 32-byte-long private key, and a 4-byte-long checksum) that it transforms into decimal notation before feeding into the base58_encode_int method. The version prefix is set to ’80’ in hexadecimal notation. The smallest and largest sequences of 74 nibbles (i.e., 37 bytes) that can be formed with a ’80’ prefix are respectively given by:
8000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 00
80FF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF FF
When these hexadecimal strings get transformed to decimal representation and then fed to base58_encode_int, we respectively obtain:
5HpHagT65TZzG1PH3CSu63k8DbpvD8s5ip4nEB3kEsreAbmahZy
5Km2kuu7vtFDPpxywn4u3NLu8iSdrqhxWT8tUKjeEXs2fDqZ9iN
Due to the nature of the base 58 encoding scheme (which works like any other base), the image of any valid string of 74 nibbles will be confined to this range, and hence is bound to start with a 5.
Private keys – WIF-compressed representation: Recall that the public key is a point on the elliptic curve defined by an abscissa and an ordinate. It can be represented in one of two ways:
- Uncompressed format, which corresponds to a full representation of the point storing both the abscissa and the ordinate. We discuss the details of uncompressed public keys in the next section.
- Compressed format, which is a shorter representation that saves space by storing the abscissa and the sign of the ordinate. Indeed, given the abscissa of a point on the elliptic curve, one can deduce two ordinates that can correspond to it (since the elliptic curve equation is quadratic in the ordinate). Moreover, we previously saw that the two points are symmetric about the
 -axis. As a result, knowing the abscissa and the sign of the ordinate is enough to recover the public key. We discuss the details of compressed public keys in the next section.
-axis. As a result, knowing the abscissa and the sign of the ordinate is enough to recover the public key. We discuss the details of compressed public keys in the next section.
Consequently, given a private key, we need a mechanism to specify whether a compressed or uncompressed public key will be derived from it. The specification is done by adding the suffix ’01’ (in hexadecimal notation) to private keys from which compressed public keys are derived. We denote by WIF-compressed the format referring to the WIF-encoded private key augmented with the ’01’ suffix (i.e., corresponding to a compressed public key). We reserve the terminology WIF to refer to WIF-encoded private keys from which uncompressed public keys are derived.
priv_key_hex_aug = priv_key_hex + '01' comp_priv_key_wif = base58Check(priv_key_hex_aug, '80') print "The WIF-compressed private key is: ", comp_priv_key_wif
comp_priv_key_wif ![]()
L1pmhZ7BRLyFSnzDBp9LnscmHGjTGujnV2aQAp3yxoH8ZuD7ZBoA
An exercise similar to the one carried for WIF-encoded keys, reveals that all WIF-compressed formats start with either ![]() or
or ![]()
Public keys – Uncompressed representation: By multiplying the private key with the elliptic curve base point ![]() we generate the corresponding public key represented by the point
we generate the corresponding public key represented by the point ![]() on the elliptic curve. To do so, we invoke the previously introduced mul_scalar method which outputs
on the elliptic curve. To do so, we invoke the previously introduced mul_scalar method which outputs ![]() in decimal format. We subsequently convert each coordinate to a 64-nibble long (i.e., 256-bit long) hexadecimal format
in decimal format. We subsequently convert each coordinate to a 64-nibble long (i.e., 256-bit long) hexadecimal format ![]() . The uncompressed representation of the public key is then simply the concatenation of the hexadecimal prefix string ’04’,
. The uncompressed representation of the public key is then simply the concatenation of the hexadecimal prefix string ’04’, ![]() and
and ![]() We will see in the next section that we use a different prefix for compressed public keys representation.
We will see in the next section that we use a different prefix for compressed public keys representation.
pub_key_dec = mul_scalar(A_dec, B_dec, p_dec, G_dec, priv_key_dec) print "\nThe uncompressed public key coordinates in decimal representation (mod p_dec) are: " print "--- Abscissa: ", pub_key_dec[0] print "--- Ordinate: ", pub_key_dec[1] uncomp_pub_key_hex = '04' + comp_256bit_hex(hex(pub_key_dec[0])) + \ comp_256bit_hex(hex(pub_key_dec[1])) print "\nThe uncompressed public key in hexadecimal representation is: " print "---", uncomp_pub_key_hex
Abscissa (i.e., ![]() ):
):
82614379957574717635004007156871918815595721887726642301310338888550373918331
Ordinate (i.e., ![]() ):
):
109303218834573473139063892787029135592762135761853446650008917532324659076912
uncomp_pub_key_hex ![]()
04 B6A6 14FE BD17 5CCA 507B 3DD1 78C8 07E0 E18B 9D76 6A80 95E9 A90C EAB0 36B4 067B F1A7
6DF3 E94D 01F5 6CA3 B3CA 4B43 829C B87A C3A4 90BA C062 1A9D 12FB FC9E 1F30
Public keys – Compressed representation: The aforementioned shorter representation of public keys consists in storing the abscissa ![]() of the public key alongside the parity of its ordinate
of the public key alongside the parity of its ordinate ![]() If the parity is even, we concatenate the hexadecimal prefix string ’02’ with
If the parity is even, we concatenate the hexadecimal prefix string ’02’ with ![]() If it is odd, we use the hexadecimal prefix string ’03’
If it is odd, we use the hexadecimal prefix string ’03’
(pub_key_dec_x, pub_key_dec_y) = pub_key_dec if (pub_key_dec_y % 2 == 0): comp_prefix = '02' else: comp_prefix = '03' comp_pub_key_hex = comp_prefix + comp_256bit_hex(hex(pub_key_dec[0])) print "\nThe compressed public key in hexadecimal representation is:" print "---", comp_pub_key_hex
comp_pub_key_hex ![]()
L1pmhZ7BRLyFSnzDBp9LnscmHGjTGujnV2aQAp3yxoH8ZuD7ZBoA
3. Bitcoin’s P2PKH and P2SH addresses
In essence, a Bitcoin address is a construct used to conveniently represent a destination of funds. It is important to highlight that an address is not a wallet and does not carry fund balances. As we will see in the post on Bitcoin transactions, whenever a particular address is used to spend some of its Bitcoins, all of its content gets debited: part of it goes to the recipient, part of it gets paid as a fee to the miner, and the remaining balance (if any) gets stored in a new address known as a change address.
Any person or entity can have as many Bitcoin addresses as they please. As a matter of fact, it is recommended to create a new address per new transaction (a practice that modern wallets implement by default).
More specifically, Bitcoin addresses are strings of alphanumeric characters that can start with either “1” or “3”. Note that there is also a new address type known as Bech32 that starts with bc1 instead. It is a segwit address but is not widely adopted ( ![]() of existing Bitcoins as of the time of this writing [2]). We will not cover it in this post and the reader interested in learning more about it can refer to e.g., [1]. Fundamentally, the two types of addresses (i.e., starting with “1” or with “3”) correspond to the following two cases:
of existing Bitcoins as of the time of this writing [2]). We will not cover it in this post and the reader interested in learning more about it can refer to e.g., [1]. Fundamentally, the two types of addresses (i.e., starting with “1” or with “3”) correspond to the following two cases:
- The destination of funds is a single recipient (person or entity) that has full control over the funds and as a result, can spend them as she pleases.
- The destination of funds is a more complex structure that specifies certain rules that need to be met in order for the funds to be spent or unlocked.
The first type is known as a Pay to Public Key Hash address or P2PKH. These addresses always start with “1”. The name rationale stems from the fact that all that is needed to create the address is a hash of the public key as we will see shortly. To spend the funds, the recipient signs a new transaction using her private key. A two-step verification mechanism is then conducted: First, the system compares the address used as a source of funds with the one derived from the signer’s public key. In case of a match, a second step validates whether the signature corresponds to the sender’s public key or not. A match would indicate that the signer is the legitimate owner and can spend the funds without further constraints. We discuss P2PKH transactions in a later post.
The second type is known as a Pay to Script Hash address or P2SH. These addresses always start with “3”. They tend to be more complex than P2PKH in the sense that certain rules must be observed in order to unlock the funds. These rules require more than the provision of a single public key hash and of a signature derived from an appropriate private key. Applicable rules or conditions are captured in a construct known as a redeem script. The P2SH name rationale stems from the fact that all that is needed to create the address is a hash of the script. An example of a script would be an M-of-N multisignature, whereby it is required to have a minimum of M out of a total of N permissible signatures in order to unlock and spend the funds associated with that address. A single entity cannot spend them and hence a single private key is not enough. We discuss P2SH transactions in a later post.
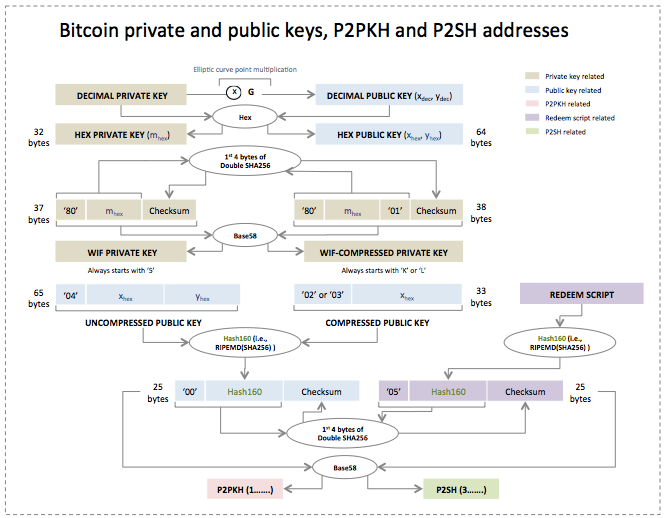
P2PKH addresses: In order to derive the Bitcoin address associated with a given public key we make use of two one-way hash functions, namely sha256 and RIPEMD-160. Whereas sha256 outputs 256-bit long digests (i.e., 32 bytes), RIPEMD160 outputs 160-bit long digests (i.e., 20 bytes). The procedure is as follows:
- Given a public key (in compressed or uncompressed format), apply sha256 on its binary representation.
- Apply RIPEMD-160 on the binary representation of the previous sha256 digest.
- Conduct Base58Check encoding on the previous digest using a version prefix of ’00’. The result is the desired Bitcoin address.
Note that the last step is similar to that used to encode private keys in WIF format. There are two differences however:
- The version prefix is set to ’00’ as opposed ’80’.
- Since adding a prefix of ’00’ does not change the integer value of the bit-sequence, we need a specifier to distinguish a string that starts with leading 0’s from one that does not. The way Base58Check does it is by mapping the leading 0-byte to a 1.
Here is a python code that generates the P2PKH addresses using a compressed or uncompressed public keys
first_sha256 = hashlib.sha256(binascii.unhexlify(uncomp_pub_key_hex)).hexdigest()
h = hashlib.new('ripemd160')# RIPEMD160 is not in core hashlib. We instantiate it separately
h.update(binascii.unhexlify(first_sha256))# Run RIPEMD160 on the binary rep of first_sha256
output = h.hexdigest()# Convert the result into hex format
uncomp_btc_add = base58Check(output, '00')
print "\nThe P2PKH Bitcoin address associated with the uncompressed public key: ", uncomp_btc_add
first_sha256 = hashlib.sha256(binascii.unhexlify(comp_pub_key_hex)).hexdigest()
h = hashlib.new('ripemd160')
h.update(binascii.unhexlify(first_sha256))
output = h.hexdigest()
comp_btc_add = base58Check(output, '00')
print "The P2PKH Bitcoin address associated with the compressed public key: ", comp_btc_add
uncomp_btc_add ![]()
1nBXeFe4ZtXMUwhJou8TbPZrPCrwtPKEm
comp_btc_add ![]()
19rAiJBZDFoV36aq6xbjtgCHNvouXKdsTw
P2SH addresses: The procedure used to derive a P2SH address is similar to that employed to derive P2PKH addresses. The difference is two-fold:
- The argument is now a redeem script as opposed to a public key (we will discuss the details of scripts in the Bitcoin transactions post)
- The version prefix is set to ’05’ as opposed to ’00’. Consequently, there is no need to add a leading 1 when conducting the Base58Check encoding.
As an example, consider the following redeem sript in hexadecimal:
52210232cfef1f9ec45bef08062640963aa8d6b15062c9c9e51c26682369969ba9101a
21029e1f52d753a7c68fb17adaa0b19f6b02f1266245186bc487c691743b6086ed5021
03d0fabbd163dd3a6ccf382b5e640622e9075f2676443499195d9b5f3e4c11993b53ae
For those interested, this script was retrieved on the blockchain (e.g., use blockchain.info) from the transaction with the following id:
38d8d5ad0fad303f7cebd9b7363f22d80f22576ba36846ae44e83ac32615472c
Here is a python code that generates the P2SH address associated with this script
part_1 = "52210232cfef1f9ec45bef08062640963aa8d6b15062c9c9e51c26682369969ba9101a"
part_2 = "21029e1f52d753a7c68fb17adaa0b19f6b02f1266245186bc487c691743b6086ed5021"
part_3 = "03d0fabbd163dd3a6ccf382b5e640622e9075f2676443499195d9b5f3e4c11993b53ae"
red_script_hex = part_1 + part_2 + part_3
first_sha256 = hashlib.sha256(binascii.unhexlify(red_script_hex)).hexdigest()
h = hashlib.new('ripemd160') # RIPEMD160 is not in core hashlib. We instantiate it separately
h.update(binascii.unhexlify(first_sha256)) # Run RIPEMD160 on the binary rep of first_sha256
output = h.hexdigest()# Convert the result into hex format
P2SH_btc_add = base58Check(output, '05')
print "\nThe P2SH Bitcoin address associated with the redeem script is: ", P2SH_btc_add
P2SH_btc_add ![]()
38ttADsJCpMuzw8M6gEdLYxBrYFHp1FmWu
An exercise similar to the one carried for WIF-encoded keys, reveals that all P2SH addresses always start with a 3.
Below is a chart summarizing the interralation between private keys, public keys, P2PKH and P2SH addresses
References
[1] Bech32.
[2] Bech32 statistics.
[3] Andrea Corbellini. Elliptic curve cryptography, a gentle introduction.

No comments
Comments feed for this article
Trackback link: https://delfr.com/bitcoin-private-key-public-key-addresses/trackback/