1. Introduction
Monero stands out from other cryptocurrencies in its ability to hide the signer, conceal the transaction amount, and protect the identity of the recepient. Parts 1, 2, 3, 4, 5, and 6 helped us build the foundation to better understand and appreciate the security properties of ring signatures (albeit in the RO model). This part (introduction to MLSAG), as well as part 8 and part 9 will focus on Monero’s privacy in so far as the signer’s identity and the transaction amount are concerned. Part 10 will introduce stealth addresses as a mechanism to protect the identity of the fund’s recipient.
In order to describe how a Monero transaction hides both the signer’s identity and the amount of the transaction, we introduce 2 additional concepts:
- A generalization of the LSAG signature (introduced in part 6) to allow each member of the ring to have a key-pair vector
![Rendered by QuickLaTeX.com [(pk_1,sk_1),.,(pk_n,sk_n)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-fc575a1ec24eb1df1f27e6a1f8aa72c1_l3.png) instead of only one pair
instead of only one pair 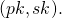
- A particular map known as the Pedersen Commitment that will be used to hide transaction amounts while allowing the network to check that input and output amounts always balance out.
Recall that by proving that a digital signature scheme was unforgeable, one gets the assurance that only the signing algorithm 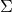 associated with a given ring member can produce a valid signature (i.e., verified by
associated with a given ring member can produce a valid signature (i.e., verified by 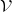 ). Any other procedure that bypasses
). Any other procedure that bypasses 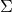 will result in a failed attempt of forgery with overwhelming probability. We note the following about the verification process of
will result in a failed attempt of forgery with overwhelming probability. We note the following about the verification process of 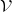 :
:
- In a “non-ring” setting, the verification is done using a particular public key
 . The validation of a given signature proves that the signer of the message (in this case user
. The validation of a given signature proves that the signer of the message (in this case user  ) knows the secret key
) knows the secret key 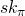 associated with
associated with  . Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (
. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (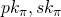 ) signed the message.
) signed the message.
- In a ring setting, the verification is conducted using a public key vector
![Rendered by QuickLaTeX.com L \equiv [pk_1,...,pk_{\pi},...,pk_n]](https://delfr.com/wp-content/ql-cache/quicklatex.com-664318b6a8929cb965e54b90a242eb5f_l3.png) known as a ring. This vector is used to conceal the identity of the signer. The validation of a given signature proves that the the signer of the message (in this case user
known as a ring. This vector is used to conceal the identity of the signer. The validation of a given signature proves that the the signer of the message (in this case user  ) knows the secret key associated with one of the public keys in
) knows the secret key associated with one of the public keys in 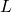 . Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (
. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair (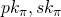 ) signed the message, for some index
) signed the message, for some index  that no one other then the actual signer knows.
that no one other then the actual signer knows.
-
The ring setting can be generalized further by allowing each ring member 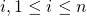 to have a key-pair vector of length
to have a key-pair vector of length 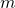 , given by
, given by ![Rendered by QuickLaTeX.com [(pk_{i}^1, sk_{i}^1),...,(pk_{i}^m, sk_{i}^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-9bbb0cc254c0adea6e1b0338b75135b0_l3.png) , as opposed to a unique key pair
, as opposed to a unique key pair 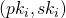 . In this setting, the verification is conducted using a public key matrix
. In this setting, the verification is conducted using a public key matrix
![Rendered by QuickLaTeX.com \[PK= \begin{bmatrix} pk_1^1 & ... & pk_{\pi}^1 & ... & pk_n^1 \\ ... & ... & ... & ... & ...\\ pk_1^m & ... & pk_{\pi}^m & ... & pk_n^m \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-753948876edb3252b45709a2a05f6024_l3.png)
The validation of the signature proves that the signer knows the secret key associated with each one of its public keys. In other terms, there exists a column in 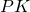 (say column
(say column  ) such that the signer knows the secret key associated with each public key appearing in that column. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair vector
) such that the signer knows the secret key associated with each public key appearing in that column. Assuming that secret keys are safe-guarded and non-compromised, this actually proves that the user with key-pair vector ![Rendered by QuickLaTeX.com [(pk_{\pi}^1,sk_{\pi}^1),...,(pk_{\pi}^m,sk_{\pi}^m)]](https://delfr.com/wp-content/ql-cache/quicklatex.com-c90b77b48be04d2c4194915758b84bbc_l3.png) signed the message, for some index
signed the message, for some index  (that no one other then the actual signer knows).
(that no one other then the actual signer knows).
Read the rest of this entry »

![Rendered by QuickLaTeX.com \[PK= \begin{bmatrix} pk_1^1 & ... & pk_{\pi}^1 & ... & pk_n^1 \\ ... & ... & ... & ... & ...\\ pk_1^m & ... & pk_{\pi}^m & ... & pk_n^m \\ \end{bmatrix} \]](https://delfr.com/wp-content/ql-cache/quicklatex.com-753948876edb3252b45709a2a05f6024_l3.png)